Что такое секущая сторона в геометрии

Секущая прямая

Секущая — это прямая, которая на некотором участке пересекает в двух точках данную кривую.

Путём приближения из секущей можно получить касательную в некоторой точке P. Если секущая определяется двумя точками пересечения с данной кривой, P и Q, где положение точки P фиксировано, а положение точки Q может изменяться, то по мере того, как точка Q приближается к точке P вдоль кривой, направление секущей приближается к направлению касательной в точке P (считаем, что первая производная кривой является непрерывной в точке P, и поэтому существует только одна касательная в этой точке). Можно сказать, что по мере того, как точка Q приближается к P, наклон секущей, или направление, в пределе приближается к наклону касательной. Эта идея является основой для геометрического определения производной.

Хорда — это участок секущей, который лежит между двумя точками пересечения с кривой.

См. также

Ссылки

Полезное

Смотреть что такое «Секущая прямая» в других словарях:

секущая — прямая Словарь русских синонимов. секущая сущ., кол во синонимов: 1 • прямая (6) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

прямая — биссектриса, параллель, линия, секущая, хорда, директриса Словарь русских синонимов. прямая сущ., кол во синонимов: 6 • биссектриса (3) • … Словарь синонимов

СЕКУЩАЯ — СЕКУЩАЯ, ей, жен. В математике: прямая, пересекающая кривую. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

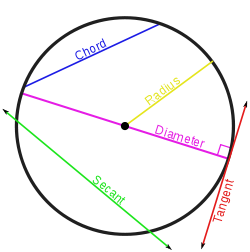
СЕКУЩАЯ — всякая прямая, имеющая с кривой линией по меньшей мере две общие точки. Отрезок секущей, лежащий внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром … Большая политехническая энциклопедия

Секущая — ж. Прямая линия, пересекающая кривую в двух или более точках. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

секущая — ой; ж. Матем. Прямая, пересекающая кривую в двух или более точках … Энциклопедический словарь

секущая — ой; ж.; матем. Прямая, пересекающая кривую в двух или более точках … Словарь многих выражений

Секанс — [лат. secans, здесь секущая (прямая); от seco режу, рассекаю], одна из тригонометрических функций (См. Тригонометрические функции); обозначение sec. В прямоугольном треугольнике С. острого угла называют отношение гипотенузы к катету,… … Большая советская энциклопедия

СЕКАНС — [лат. secans, здесь: секущая (прямая), от seco режу, рассекаю] одна из тригонометрических функций … Большой энциклопедический политехнический словарь

Касательная — прямая, с которою стремится совпасть секущая, проведенная через две точки на произвольной кривой по мере сближения этих точек. Математическая теория К. имеет весьма важное значение (см. Дифференциальное исчисление). Точка, через которую к кривой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Хорда, секущая, касательная

Определения

Хорда – отрезок, соединяющий две точки окружности.

Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Свойства

Радиус, проведенный в точку касания, перпендикулярен касательной

Отрезки касательных, проведенных к окружности из одной точки, равны.

Отрезки пересекающихся хорд связаны соотношением:

Произведения отрезков секущих, проведенных из одной точки, равны:

Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки:

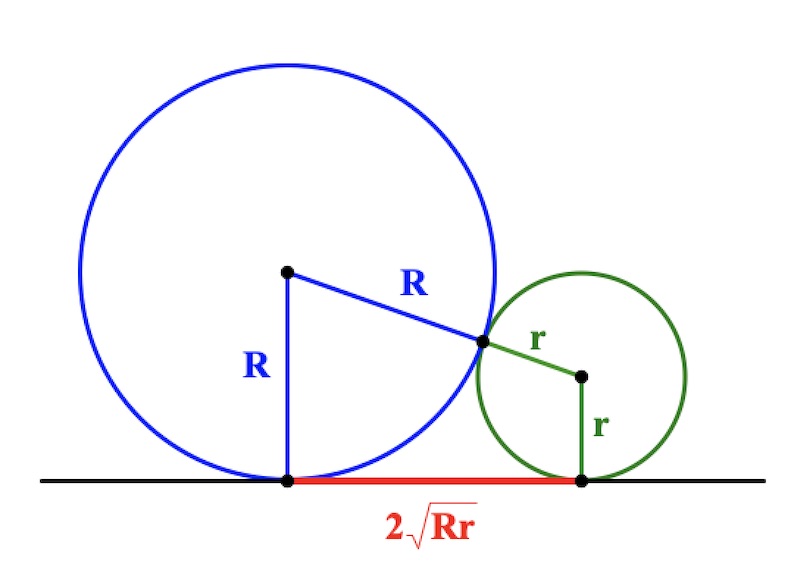
Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов Видеодоказательство

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Касательная и секущая к окружности

На плоскости прямая и окружность могут либо пересекаться друг с другом, либо не пересекаться:

Расстояние от центра O до прямой m равно длине перпендикуляра OA. Следовательно, расстояние от центра окружности до прямой всегда будет равно перпендикуляру, опущенному из центра окружности на прямую.

Если расстояние от центра окружности до прямой больше радиуса данной окружности, то прямая и окружность не пересекаются и не имеют общих точек:

Касательная

Если расстояние от центра окружности до прямой равно радиусу данной окружности, то прямая касается окружности и они имеют одну общую точку, такая прямая называется касательной к окружности:

Прямая m — касательная. Точка соприкосновения прямой и окружности, то есть их общая точка, называется точкой касания: точка A — точка касания.

Касательная – это прямая линия, имеющая с окружностью одну общую точку.

Секущая

Если расстояние от центра окружности до прямой меньше радиуса данной окружности, то прямая пересекает окружность и они имеют две точки касания, такая прямая называется секущей к окружности:

Секущая – это прямая линия, имеющая с окружностью две общие точки.

Источник

Секущая и хорда окружности (ЕГЭ 2022)

Зачем что-то знать о секущих и хордах в окружности?

Как обычно, знание свойств и закономерностей сильно облегчает жизнь.

Зная свойства секущих и хорд в окружности и закономерности (формулы), мы сможем решить многие задачи на ЕГЭ!

Секущая и хорда окружности — коротко о главном

Секущая окружности

Здесь \( \displaystyle AC\) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.

Хорда окружности

Здесь \( \displaystyle BC\) – хорда окружности – отрезок, соединяющий две точки на окружности.

Длина хорды

Пусть \( \displaystyle AB\) – хорда, \( \displaystyle R\) – радиус, \( \displaystyle \angle AСB\) – любой вписанный угол, опирающийся на хорду \( \displaystyle AB\). Тогда:

\( \displaystyle AB=2R\sin \alpha\).

Произведение длин отрезков хорд и секущих

Для любых двух хорд, проходящих через некоторую точку \( \displaystyle A\), выполняется:

\( \displaystyle AB\cdot AC=AD\cdot AE\).

Теорема о секущей и касательной

Для любых секущей и касательной, проходящих через точку \( A\), верно:

\( \displaystyle A<^<2>>=AD\cdot AE\).

А теперь подробнее…

Определения секущей и хорды окружности

Давай прежде всего вспомним, что такое секущая и хорда. Смотри на картинки.

Здесь \( \displaystyle AC\) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.

Здесь \( \displaystyle BC\) – хорда окружности – отрезок, соединяющий две точки на окружности.

Кстати, заметил ли ты, что на первом рисунке хорда \( \displaystyle BC\) является кусочком секущей \( \displaystyle AC\)?

Вот так всегда и бывает: если есть секущая, то один её кусок – хорда, а второй называется внешняя часть, ну, как у нас \( \displaystyle AB\) – она же снаружи, верно?

Что же мы должны знать о секущей и хорде окружности?

Всего-то 2-3-4 утверждения. Давай начнём с того, что ты, возможно, уже читал в разделе «Теорема синусов» и «Теорема косинусов» — с длины хорды в окружности.

Длина хорды окружности

Пусть \( \displaystyle AB\) – хорда, \( \displaystyle R\) – радиус, \( \displaystyle \angle ACB\) – любой вписанный угол, опирающийся на хорду \( \displaystyle AB\).

Тогда \( \Large\frac<\sin \alpha >=2R\)

Узнал теорему синусов?

Значит, длину хорды окружности можно найти по формуле:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Произведение длин отрезков хорд и секущих

Сейчас мы сформулируем очень важное, пожалуй, даже основное свойство хорд и секущих окружности.

Словами это свойство формулировать неудобно – получается длинно и некрасиво, поэтому ограничимся буквами.

Произведение длин отрезков хорд окружности

Для любых двух хорд окружности, проходящих через некоторую точку \( \displaystyle A\), выполняется: \( \displaystyle AB\cdot AC=AD\cdot AE\)

Произведение длин отрезков секущих окружности

Для любых двух секущих, проходящих через некоторую точку \( \displaystyle A\), выполняется: \( \displaystyle AB\cdot AC=AD\cdot AE\)

Вопрос первый: Почему мы сформулировали утверждения друг под другом столбиком?

Ответ: Утверждения очень похожи – если закрыть картинки и слова, то получится просто одно и то же – удивительно, не правда ли? Ну, и это сходство гораздо лучше видно, когда утверждения стоят рядом.

Вопрос второй: Как не перепутать, что на что умножать?

Источник

Касательная к окружности

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

Докажем, что касательная и радиус АВ перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

Поскольку ∠АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, ⌒АВ = 62°.

Если провести две касательных к окружности из одной точки, то их отрезки от этой начальной точки до точки касания будут равны.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично должны быть равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

sin BDA = AB : AD = 4,5 : 9 = 0,5

Мы знаем, что прямая, проложенная из точки до центра окружности, делит угол между касательными, проложенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN между ними равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности опускаются две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

Сократим уравнение на (у + R) и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ ⌒АВ.

⌒АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

⌒КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

Источник

• ← Что такое секущая рамка
• Что такое секущиеся волосы →