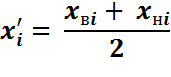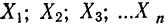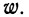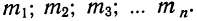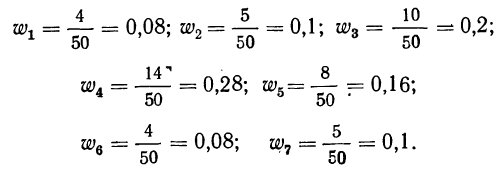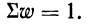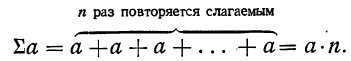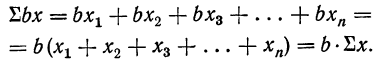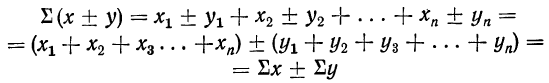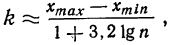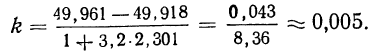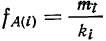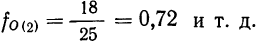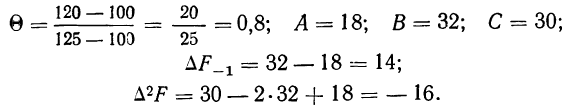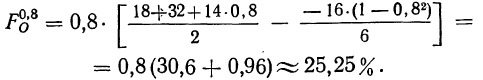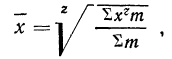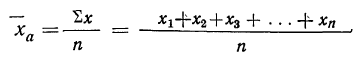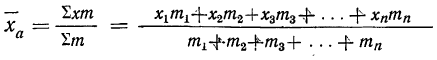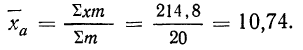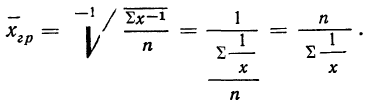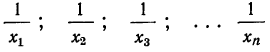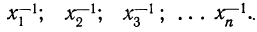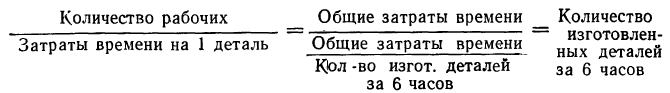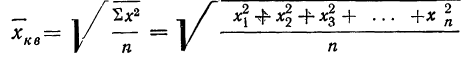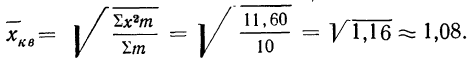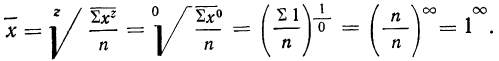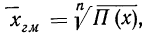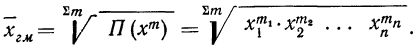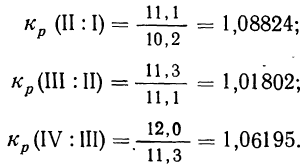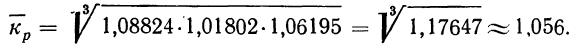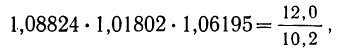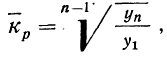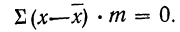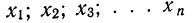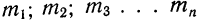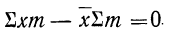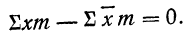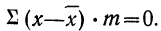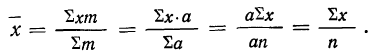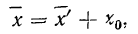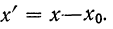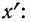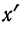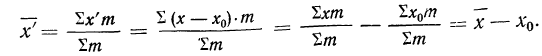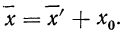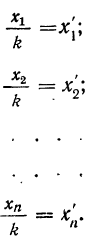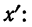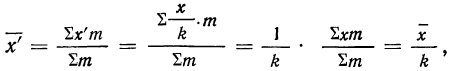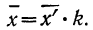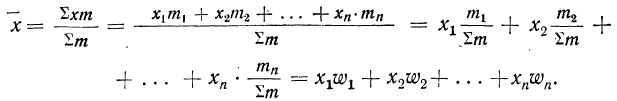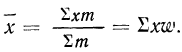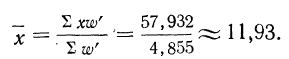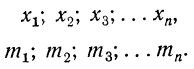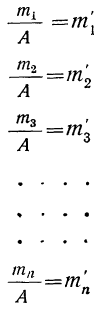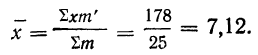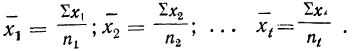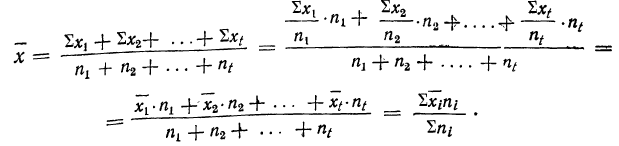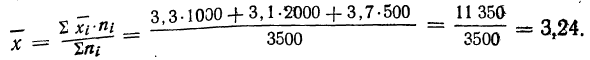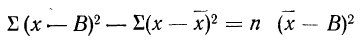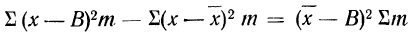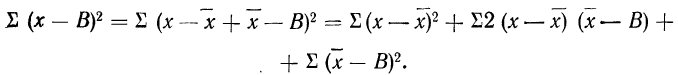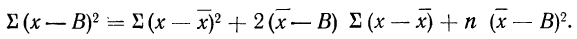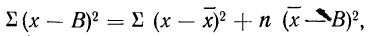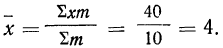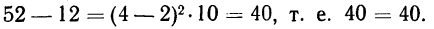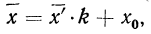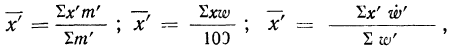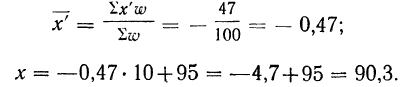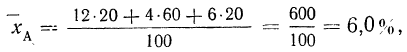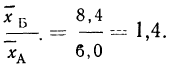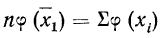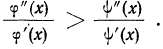Что такое середина интервала

Решение задач по статистике и выводы к ним

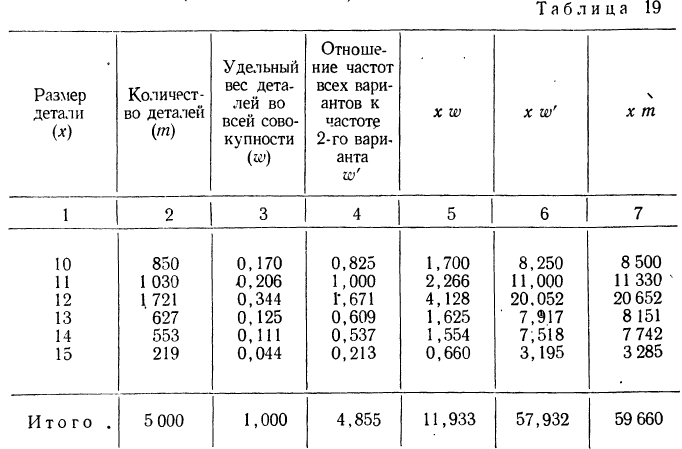
Задача по статистике №1. Найти параметры интервального ряда распределения по данным таблицы, а именно: моду, медиану, среднюю арифметическую величину, среднюю взвешенную величину, коэффициент вариации, среднее квадратическое отклонение.

Группы компаний по основным производственным фондам, млн. руб. (х)

Середина интервала (Xi) = (начало интервала+конец интервала)/2

Мы сразу добавили столбец «середина интервала». Для первой группы компаний рассчитали следующим образом: (10+25)/2=17,5 млн. руб. Для 2-5 групп расчеты произведены аналогично.

Теперь рассчитаем среднюю арифметическую величину.

средняя арифметическая = = (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.

Далее рассчитаем среднюю взвешенную величину.

средняя взвешенная = = (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.

Значение средневзвешенной величины можно считать более корректным, чем значение средней арифметической величины, поэтому далее в расчетах будем использовать среднюю взвешенную.

Теперь добавим в таблицу столбцы, данные которых нам понадобятся для расчета дисперсии.

Середина интервала (Xi) = (начало интервала+конец интервала)/2

Источник

Определяем середины интервалов

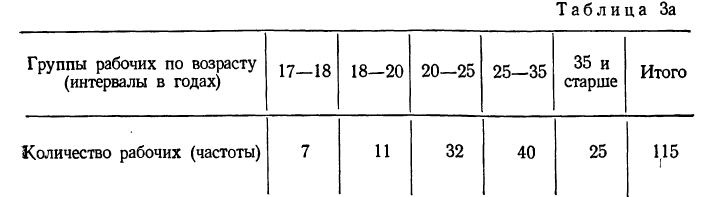
Рассмотрим на примере с ростом детей, как построить интервальный ряд с равными интервалами.

Имеются первоначальные данные.

90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 92, 93, 94, 95, 96, 98, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 100, 101, 102, 104, 110, 112, 114, 116, 117, 120, 122, 123, 124, 129, 110, 111, 113, 115, 116, 117, 121, 125, 126, 127, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 111, 113, 116, 127, 123, 122, 130, 131, 132, 133, 134, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 131, 133, 135, 136, 138, 139, 140, 141, 142, 143, 145, 146, 147, 148

Источник

Содержание:

В результате статистической обработки материалов, полученных при измерении величины явления, можно подсчитать число единиц, обладающих конкретным значением того или иного признака.

Условились каждое отдельное значение признака обозначать

Если мы расположим отдельные значения признака (варианты) в возрастающем или убывающем порядке и укажем относительно каждого варианта, как часто он встречался в данной совокупности, то получим распределение признака, или вариационный ряд.

Вариационные ряды и их характеристики

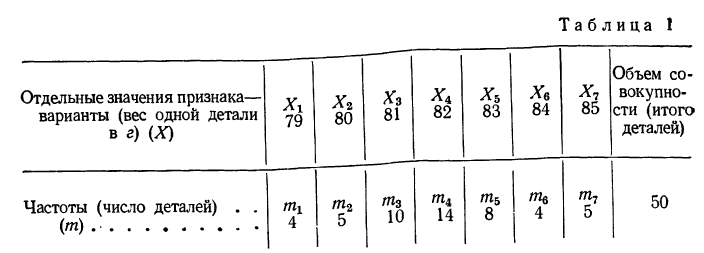
Построим вариационный ряд для приведенного выше примера. Для этого находим наименьший вариант, равный 79 г, и, располагая варианты в возрастающем порядке, подсчитываем их частоту. Так, вариант 79 г встречается 4 раза, вариант 80 г — 5 раз и т. д. Расположим полученные варианты следующим образом (см. табл. 1).

Такой ряд называется вариационным рядом; он характеризует изменение (варьирование) какого-нибудь количественного признака (в нашем примере варьирование веса деталей). Следовательно, вариационный ряд представляет собой две строки (или колонки). В одной из них приводятся варианты, а в другой частоты.

Виды вариации

Вариация признака может быть дискретной и непрерывной. Дискретной вариацией признака называется такая, при которой отдельные значения признака (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число), т. е. даны в виде прерывных чисел. Непрерывной называется вариация, при которой значения признака могут отличаться одно от другого на сколь угодно малую величину. В качестве примера можно привести: для дискретной вариации признака — число станков, обслуживаемых одним рабочим, число семян в 1 кг и т. д.; для непрерывной вариации признака— процент выполнения рабочим нормы выработки, вес одного семени и т. д.

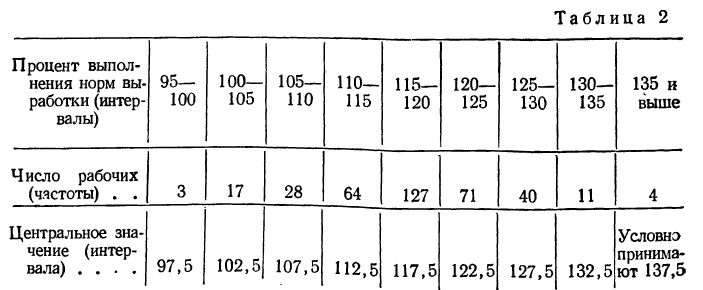
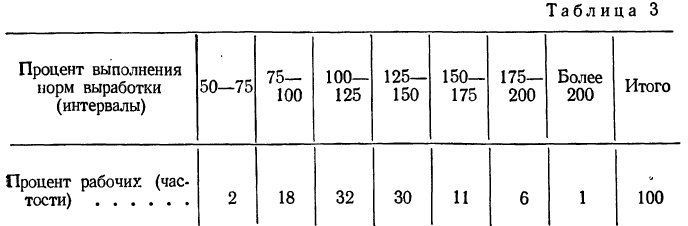
При непрерывной вариации распределение признака называется интервальным. Частоты относятся не к отдельному значению признака, как это бывает при дискретной вариации, а ко всему интервалу. Часто за значение интервала принимают его середину, т. е. центральное значение. В качестве примера можно привести интервальный вариационный ряд по проценту выполнения норм выработки.

Пример 1.

Распределение рабочих по проценту выполнения норм выработки.

Частость

Нередко вместо абсолютных значений. частот используют относительные величины. Для этой цели можно использовать долю частоты того или иного варианта (а также интервала) в сумме всех частот. Такая величина называется частостью и обозначается

Мы имеем частоты

Для получения суммы всех частот их нужно сложить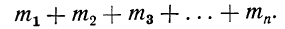

В математике используется знак 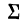(греческая буква сигма заглавная), означающий суммирование.

Следовательно, можно записать: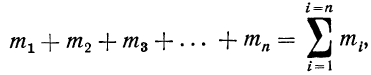

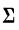
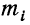
где значки 1=1 и i=n под и над показывают, что суммированию подлежат все при условии, что i принимает все целые значения от 1 до n.

В дальнейшем в подобных случаях (т. е. при суммировании по подстрочному номеру i) мы не будем записывать значения, принимаемые i, но будем помнить смысл записи 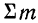(уже без указания значений, принимаемых i).

Для получения частости каждого варианта или интервала-нужно его частоту разделить на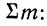
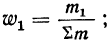
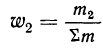
и т.д.,
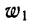
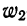
где — частость первого варианта или интервала, — второго и т. д.

Вычислим частости, используя данные табл. 1:

Сумма всех частостей равна 1:

В нашем примере
0,08+0,1+0,2+0,28+0,16+0,08+0,1 = 1,00.
Частости можно выражать и в процентах (тогда сумма всех частостей равна 100%).

Границы интервалов

В интервальном вариационном ряду в каждом интервале различают нижнюю и верхнюю границы интервала:

При построении интервальных вариационных рядов в каждый интервал включаются варианты, числовые значения которых больше нижней границы и меньше или равны верхней грани це. Так, в табл.12 в интервал 95—100% попадают все рабочие, выполнившие нормы выработки от 95 до 100% включительно. Рабочие, выполнившие план на 100,01%, попадают в следующий интервал. Разумеется надо стремиться строить интервалы так, чтобы избегать попадания значительного числа случаев на границы интервалов.

Интервальные вариационные ряды бывают с одинаковыми и неодинаковыми интервалами. В последнем случае чаще всего встречаются интервалы последовательно увеличивающиеся.

Пример 2.

Вариационный ряд с равными интервалами:

Пример 2а.

Вариационный ряд с последовательно увеличивающимися интервалами:

Свойства сумм

Как видно (и из дальнейшего изучения материала), нам приходится иметь дело с суммами. Рассмотрим некоторые свойства сумм.

1) Сумма ограниченного числа слагаемых, имеющих одну и ту же величину (сумма постоянной), равна произведению величины слагаемых на их число:

2) Постоянный множитель может быть вынесен из-под знака суммы и введен под знак суммы:

3) Сумма алгебраической суммы нескольких переменных равна алгебраической сумме сумм каждой переменной:

(легко обобщается на большее число слагаемых).

Величина интервала

Для выбора оптимальной величины интервала, т. е. такой величины интервала, при которой вариационный ряд не будет очень громоздким и в нем не исчезнут особенности явления, можно рекомендовать формулу:

где n — число единиц в совокупности.

Так, если в совокупности 200 единиц наибольший вариант равен 49,961, а наименьший — 49,918, то

Следовательно, в данном случае оптимальной величиной интервала может служить величина 0,005.

Плотность распределения

В качестве характеристики ряда распределения применяют плотность распределения, которую вычисляют как отношение-частот или частостей к величине интервала.

Различают абсолютную плотность распределения:

и относительную плотность распределения: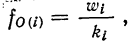

где 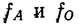-— плотности распределения, абсолютная (со значком А) и относительная (со значком О).

Пример 3.

По данным примера 2 вычислим относительную плотность распределения. Для первого интервала

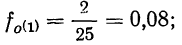
для второго интервала

Расщепление интервалов

Часто возникает необходимость в расщеплении интервалов. Для этой цели можно воспользоваться следующим методом для интервальных вариационных рядов с равными интервалами.

Расщепление производится при предположении, что плотность вариационного ряда изменяется по параболе второго порядка. Имеется в виду, что весь интервал разбивается на две части: первую, составляющую долю в величине интервала, и вторую 1—. Соответственно частость расщепляемого интервала F распадается на В этом случае:

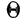
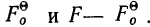
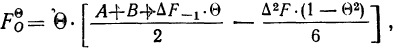
где А — частость интервала, предшествующего расщепляемому;

В — частость расщепляемого интервала;

С — частость интервала, последующего за расщепляемым;

— приращение частости интервала, предшествующего расщепляемому ();

— второе приращение частостей — (В—А)=С—2В+А].

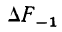
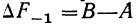
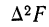
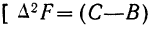
Пример 4.

По данным примера 2 произведем расщепление интервала 100—125% на две части, выделим часть интервала 100—120% и определим удельный вес рабочих, выполняющих норму выработки от 100 до 120%.

Имеем:

Получаем частость по соответствующей формуле:

В случае неравных интервалов вычисление усложняется.

Графические методы изображения вариационных рядов

Большое значение для наглядного представления вариационного ряда имеют графические методы его изображения. Вариационный ряд графически может быть изображен в виде полигона, гистограммы, кумуляты и огивы.

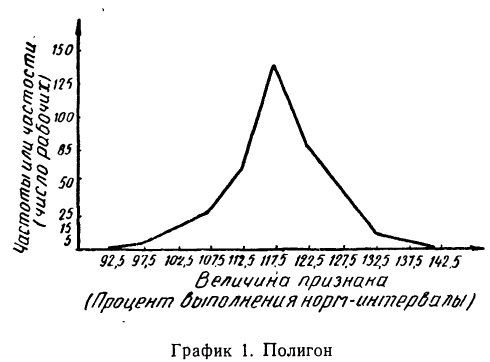
На оси абсцисс отмечаются точки, соответствующие, величине вариантов, и из них восстанавливаются ординаты (перпендикуляры), длина которых соответствует численности этих вариантов. Вершины ординат соединяются прямыми линиями. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но могут быть применены и для интервальных рядов. В этом случае ординаты, пропорциональные частоте или частости интервала, восстанавливаются перпендикулярно оси абсцисс в точке, соответствующей середине данного интервала. Для замыкания крайние ординаты соединяются с •серединой интервалов, в которых частоты или частости равны нулю.

Пример 5.

По данным примера 1 строим полигон.

Гистограмма распределения строится аналогично полигону в прямоугольной системе координат. В отличие от полигона при построении гистограммы на оси абсцисс берутся не точки, а отрезки, изображающие интервал, а вместо ординат, соответствующих частотам или частостям отдельных вариантов, строят прямоугольники с высотой, пропорциональной частотам или частостям интервала.

В случае неравенства интервалов гистограмма распределения строится не по частотам или частостям, а по плотности интервалов (абсолютной или относительной). При этом общая площадь гистограммы равна численности совокупности, если построение производится по абсолютной плотности, или единице, если гистограмма построена по относительной плотности.

Если соединить прямыми линиями середины верхних сторон прямоугольников, то получим полигоны распределения.

Разбивая интервалы на несколько частей и исходя из того, что вся площадь гистограммы должна остаться при этом неизменной, можно получить мелкоступенчатую гистограмму, которая в пределе (за счет уменьшения величины интервала) перейдет в плавную кривую, называемую кривой распределения.

Пример 6.

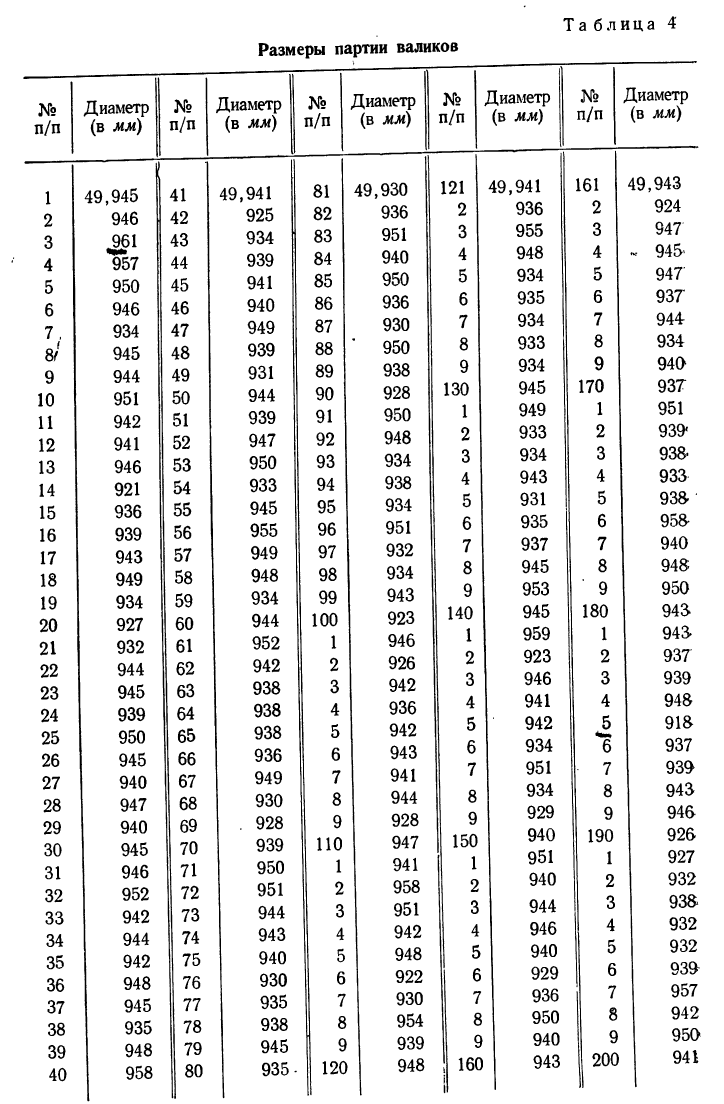
Имеются данные о диаметре 200 валиков (см. табл. 4).

Чтобы по этим данным построить вариационный ряд с равными интервалами, изобразить его с помощью гистограммы, а затем превратить ее в мелкоступенчатую, производим следующие действия:

а) Выбираем наименьший вариант, а затем наибольший и находим между ними разность. Делим полученную разность на число проектируемых интервалов и получаем величину каждого интервала.

Так, наименьший интервал 49,918, наибольший — 49,961. Разность 49,961—49,918=0,043.

Допустим, мы хотим получить пять интервалов, тогда величина каждого интервала равна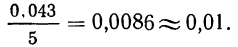

Следовательно, будем иметь такие интервалы:

49,918—49,928; 49,928—49,938 и т. д.

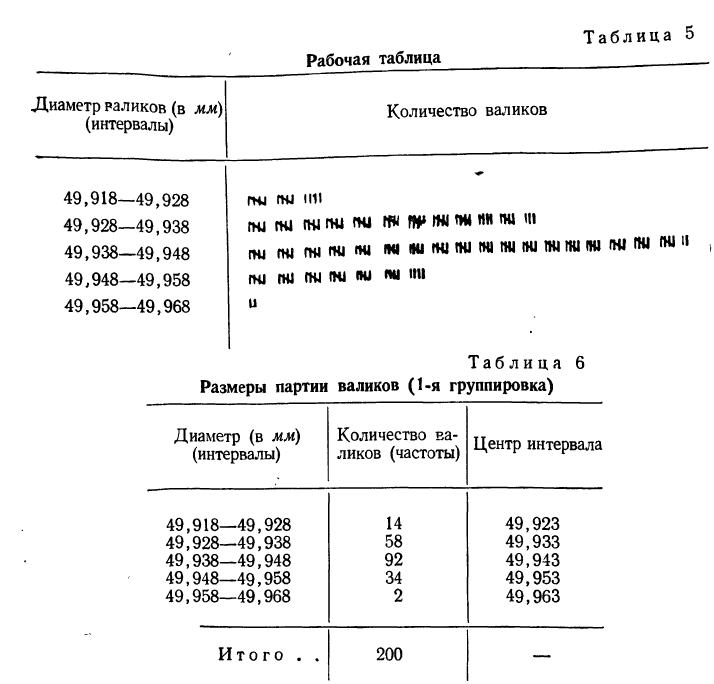
На основании рабочей таблицы получаем следующий вариационный ряд (см. табл. 6).

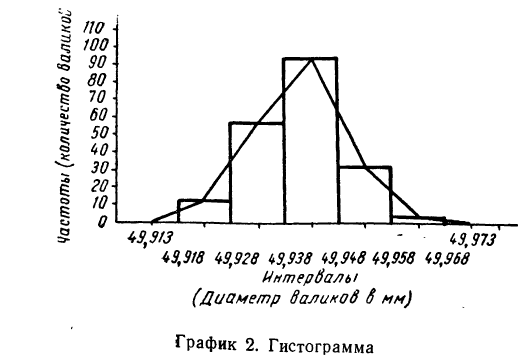
б) По полученному вариационному ряду строим гистограмму распределения: на оси абсцисс откладываем диаметры валиков, начиная с 49,918 до 49,968, а на оси ординат проставляем масштаб; далее строим прямоугольники с высотой, пропорциональной количеству валиков в каждом интервале.

Соединяем прямыми линиями середины верхних сторон прямоугольников и получаем полигон (см. график 2).

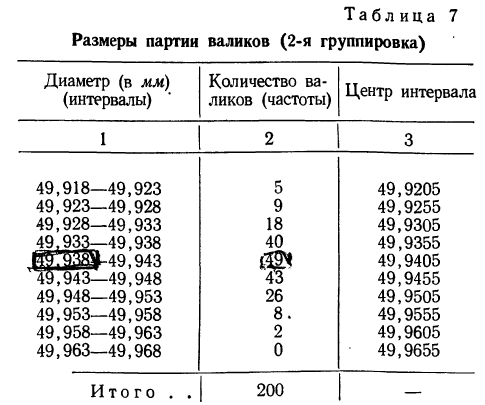
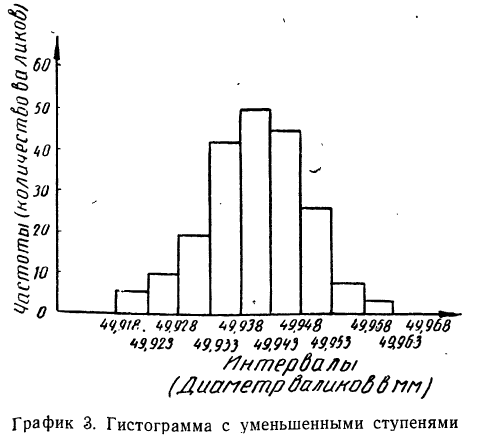
Для получения мелкоступенчатой гистограммы разбиваем интервалы на две равные части и получаем:

Если построить гистограмму по новому вариационному ряду, с уменьшенными интервалами, то получим гистограмму с более мелкими ступенями. Учет требования о неизменности площади гистограммы приводит к необходимости увеличить масштаб оси ординат вдвое.

Можно продолжить процесс расчленения интервалов и дальше, получая все более и более мелкоступенчатую гистограмму.

Кумулятивная кривая (кривая сумм — кумулята) получается при изображении вариационного ряда с накопленными частотами или частостями в прямоугольной системе координат. При построении кумуляты дискретного признака на ось абсцисс наносятся значения признака (варианты). Ординатами служат вертикальные отрезки, длина которых пропорциональна накопленной частоте или частости того или иного варианта. Соединением вершин ординат прямыми линиями получаем ломаную (кривую) кумуляту.

Пример 7.

По данным табл. 4 построить кумуляту.

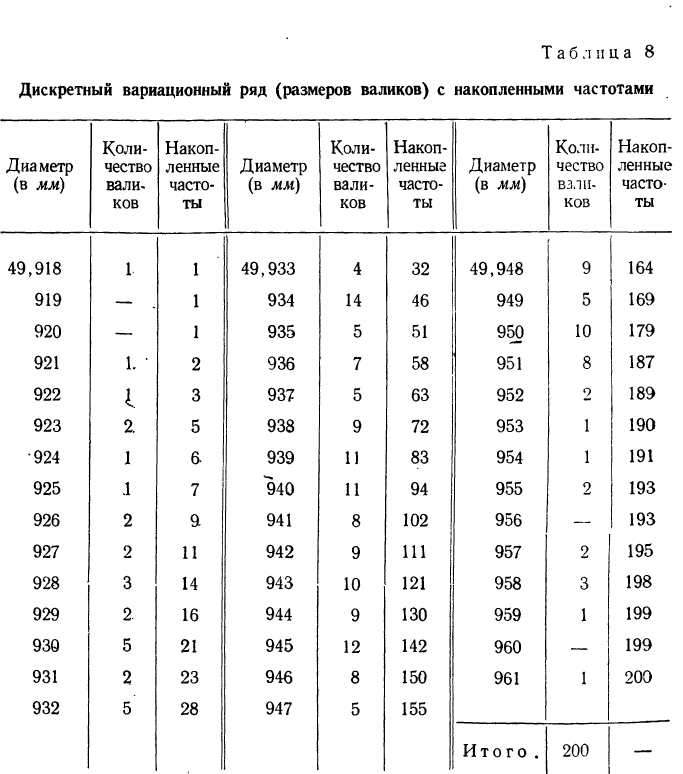
Составляем дискретный вариационный ряд с накопленными частотами (при наличии частостей можно для построения кумуляты пользоваться ими; см. табл. 8).

Накопленная частота определенного варианта получается суммированием всех частот вариантов, предшествующих данному, с частотой этого варианта.

Используя накопленные частоты, строим кумуляту.

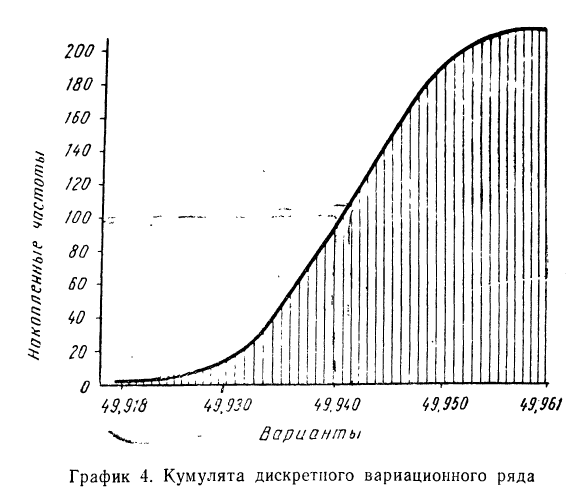
При построении кумуляты- интервального вариационного ряда нижней границе первого интервала соответствует частота, равная нулю, а верхней границе — вся частота интервала. Верхней границе второго интервала соответствует накопленная частота первых двух интервалов (т. е. сумма частот этих интервалов) и т. д. Верхней границе последнего (максимального) интервала соответствует накопленная частота, равная сумме всех частот.

Пример 8.

По данным табл. 7 построить кумуляту.

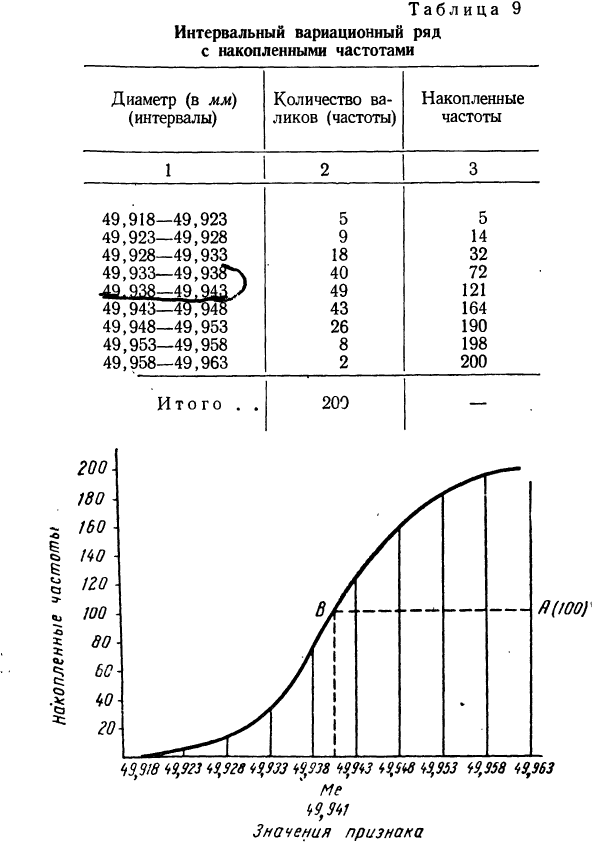
Составляем интервальный вариационный ряд с накопленными частотами (см. табл. 9). По полученным накопленным частотам строим кумуляту (см. график 5).

Огива строится аналогично кумуляте с той лишь разницей, что на ось абсцисс наносят накопленные частоты, а на ось ординат — значения признака. Если лист бумаги, на котором изображена кумулята, повернуть на 90° и посмотреть на него с обратной стороны на свет, то можно увидеть огиву.

График 5. Кумулята интервального вариационного ряда

Пример 9. По данным табл. 9 построим огиву (см. график 6)-

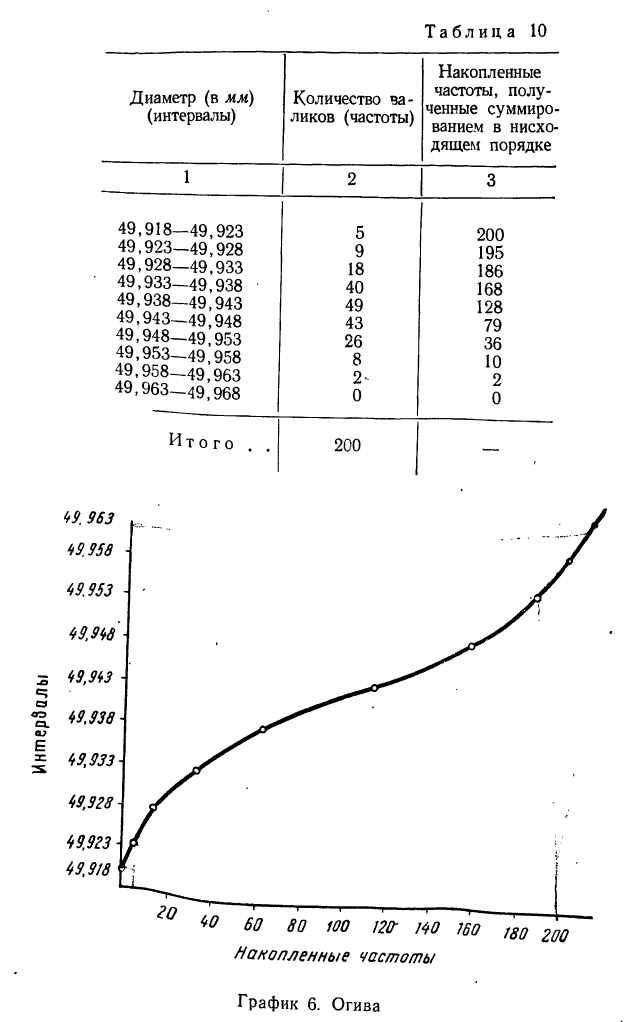
Накопленные частоты можно получать не только в восходящем порядке, но и в нисходящем, тогда частоты вариантов суммируются снизу вверх.

Пример 10.

По данным табл. 7. вычислить накопленные частоты в нисходящем порядке.

Средние величины

В качестве одной из важнейших характеристик вариационного ряда применяют среднюю величину. Математическая статистика различает ряд типов средних величин: арифметическую, геометрическую, гармоническую, квадратическую, кубическую и др. Все перечисленные типы средних могут быть исчислены для случаев, когда каждый из вариантов вариационного ряда встречается только один раз, — тогда средняя называется простой или невзвешенной, — и для случаев, когда варианты или интервалы повторяются различное число раз. При этом число повторений вариантов или интервалов называют частотой или статистическим весом, а среднюю, вычисленную с учетом статистического веса, —взвешенной средней.

Выбор одного из перечисленных типов средних для характеристики вариационного ряда производится не произвольно, а в зависимости от особенностей изучаемого явления и цели, для которой средняя исчисляется.

Практически при выборе того или другого типа средней следует исходить из принципа осмысленности результата при суммировании или при взвешивании. Только тогда средняя применена правильно, когда в результате взвешивания или суммирования получаются величины, имеющие реальный смысл.

Обычно затруднения при выборе типа средней возникают лишь в использовании средней арифметической или гармонической. Что же касается геометрической и квадратической средних, то их применение ограничено особыми случаями (см. далее).

Степенная средняя

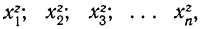
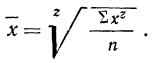
Все указанные типы средних величин могут быть получены из формул степенной средней. Если имеются варианты то средняя из вариант тов может быть исчислена по формуле простой невзвешенной степенной средней порядка z

При наличии соответствующих частот 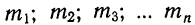средняя исчисляется по формуле взвешенной степенной средней

где 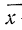— степенная средняя;

z — показатель степени, определяющий тип средней;

m — частоты или статистические веса вариантов.

Средняя арифметическая получается из формулы степенной средней при подстановке z=1

средняя арифметическая невзвешенная и

средняя арифметическая взвешенная.

Пример 11.

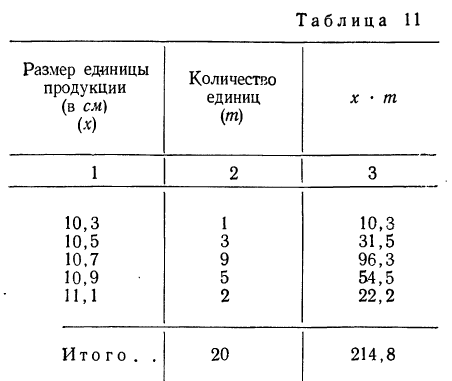
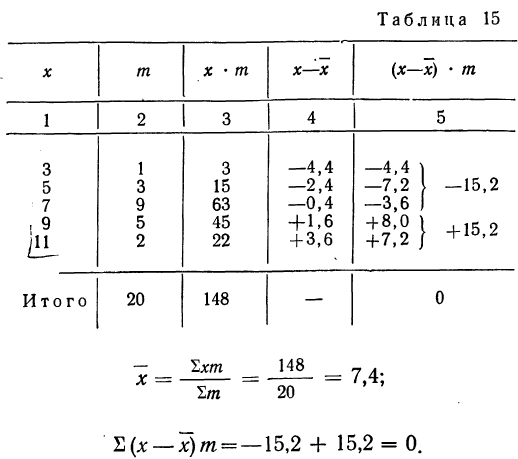
Измерения 20 единиц продукции дали следующие результаты (колонки 1 и 2):

Вычислить средний размер единицы продукции.

Находим среднюю арифметическую. Для этого исчисляем в табл. 11 колонку 3

Здесь умножение значения признака на вес и суммирование этих произведений дает общий размер продукции, т. е. имеет реальный смысл.

Средняя гармоническая получается при подстановке в формулу степенной средней значения z =—1.

Средняя гармоническая простая

Средняя гармоническая взвешенная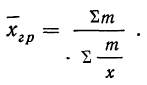

Средняя гармоническая вычисляется в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, т. е. когда суммированию подлежат не сами варианты, а обратные им величины

Пример 12.

По следующим данным о работе 22 рабочих в течение 6 часов вычислить среднюю гармоническую взвешенную.

В данном случае взвешивание состоит в делении по каждой группе количества рабочих (m) на затраты времени по изготовлению одной детали (х). Для проверки правильности выбора типа средней осмыслим результат взвешивания. Исходя из того, что все рабочие работали по 6 часов, количество рабочих можно рассматривать как величину, определяющую общие затраты времени. Тогда результат деления представит вполне осмысленную величину:

Таким образом, средняя гармоническая в данном примере применена правильно. При использовании средней гармонической для упрощения расчетов целесообразно пользоваться таблицами обратных чисел (см. приложение VIII).

Средняя квадратическая получается из формулы степенной средней при подстановке z=2

средняя квадратическая невзвешенная и

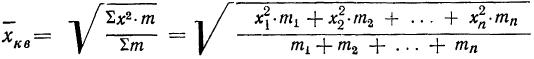
средняя квадратическая взвешенная.

Средняя квадратическая используется только в тех случаях, когда варианты представляют собой отклонения фактических величин от их средней арифметической или от заданной нормы.

Пример 13.

Имеются результаты измерения отклонений фактической длины изделий от заданной нормы.

Вычислим среднюю величину отклонений.

Находим среднюю квадратическую взвешенную; для этого исчисляем в табл. 13 колонки 3 и 4:

Значит, средняя величина отклонений фактической длины изделий от заданной нормы составляет 1,08 мм. В данном случае средняя арифметическая была бы непригодна, так как в результате мы получили бы нуль

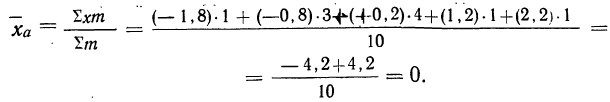
Средняя геометрическая получается из формулы степенной средней при подстановке z=0:

Для раскрытия неопределенности этого вида прологарифмируем обе части равенства: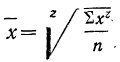

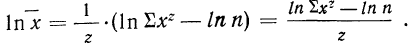
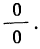
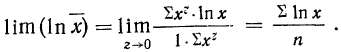
Теперь при подстановке z в правую часть равенства получаем неопределенность вида Используя правило Лопиталя и дифференцируя отдельно числитель и знаменатель по переменной z, получаем:

Таким образом:

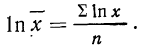
Потенцируя, находим среднюю: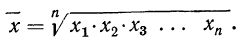

Это и есть формула средней геометрической невзвешенной, которая записывается сокращенно так:

где П — знак произведения;

n — число вариантов.

Если использовать частоты (m), то средняя геометрическая взвешенная примет следующий вид:

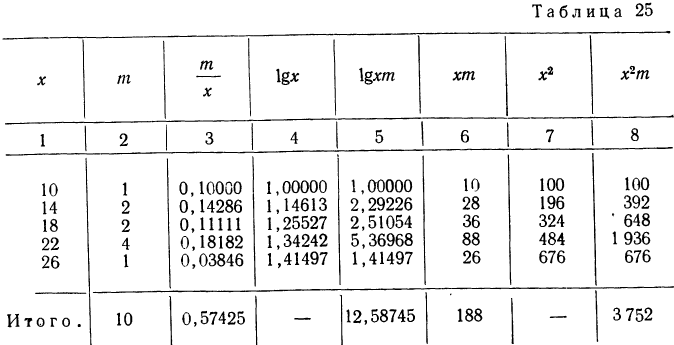
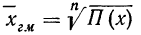
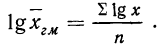
Вычисления средней геометрической в значительной мере упрощаются применением логарифмирования. Для невзвешенной средней геометрической получаем:

Для взвешенной средней геометрической: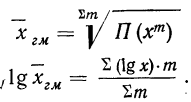

Таким образом, логарифм средней геометрической есть средняя арифметическая, из логарифмов вариантов (см. формулы средней арифметической).

Средняя геометрическая используется главным образом при изучении динамики (см. раздел II).

Расчет средних коэффициентов и темпов. роста производится по формулам средней геометрической.

Пример 14.

Выпуск промышленной продукции производился предприятием в следующих размерах:

Чтобы найти средний месячный коэффициент и темп роста промышленной продукции, определяем помесячные коэффициенты роста 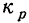, которые в данном случае и являются вариантами:

Из найденных трех помесячных коэффициентов роста (вариантов) определяем средний месячный коэффициент роста 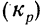по формуле средней геометрической. Для этого найденные коэффициенты роста перемножаются и из произведения извлекается корень третьей степени

Из разобранного примера можно сделать два вывода: во-первых, что произведение трех найденных коэффициентов роста можно получить без их предварительного исчисления путем деления апрельского объема продукции (12,0) на январский объем (10,2):

и, во-вторых, что показатель степени корня, равный трем (число коэффициентов роста), можно получить вычитанием единицы из числа приведенных в примере месяцев (четыре).

Таким образом, наиболее удобной для исчисления среднего коэффициента роста следует считать формулу:

где n — число приведенных дат или периодов;

— последний член ряда;

— первый член ряда.

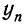
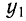
Математические свойства средней арифметической

Из вышеуказанных средних наиболее часто применяется средняя арифметическая. Знание свойств средней арифметической позволяет упрощенно ее вычислять.

Математические свойства средней арифметической:

1) Средняя постоянной величины равна этой же постоянной

2) Сумма отклонений от средней, умноженных на веса (частоты), равна нулю:

(если все веса равны единице)
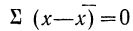
или

Докажем это свойство для средней взвешенной.

Имеем: варианты

частоты

откуда

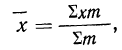
и

Подводя под общий знак суммы, получаем:

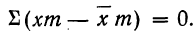
Следовательно,

Пример 15.

Вычислить среднюю (по колонкам 1 и 2) и убедиться в правильности выведенной формулы.

3) Если у всех вариантов х частоты m равны друг другу, то средняя арифметическая взвешенная равна средней арифметической невзвешенной.

Имеем

4) Если из всех вариантов (х) вычесть постоянную величину и из результатов вычитания, т. е. из отклонений вариантов от этой постоянной величины вычислить среднюю то она окажется меньше искомой средней на эту постоянную величину Поэтому, чтобы получить среднюю из вариантов нужно к найденной средней прибавить ту же постоянную величину: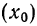

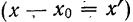
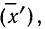
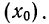
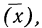
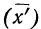
если

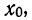
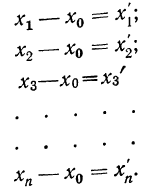
Имеем отклонения от постоянной величины обозначенные

Находим среднюю из

Откуда

Пример 16.

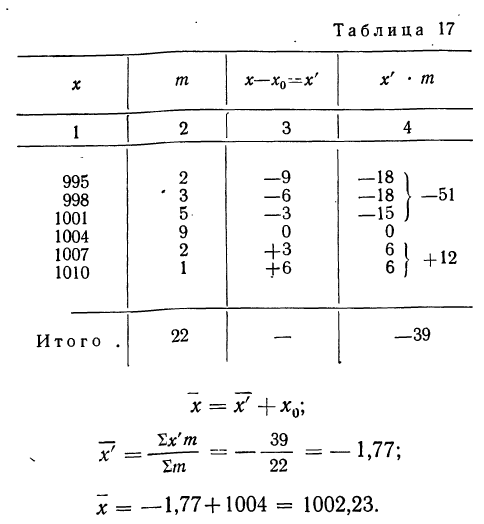
Вычислить среднюю путем вычитания 1000 из всех вариантов по следующим данным (колонки 1 и 2).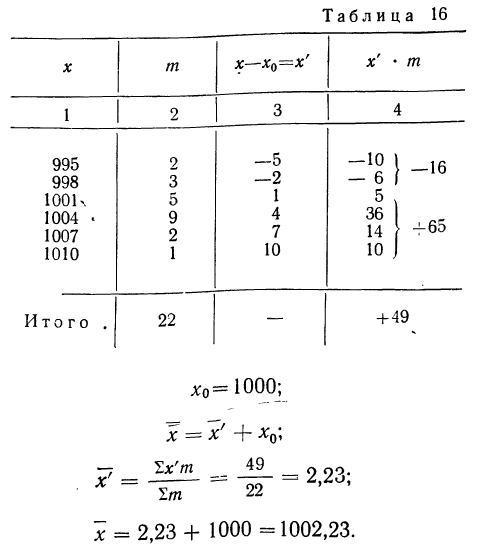
.

Пример 17.

Используя данные прёдыдущего примера, можно убедиться, что если за 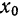взять не 1000, а 1004, то величина средней не изменится.

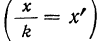
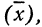
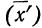
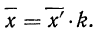
5) Если все варианты (х) уменьшить в одно и то же число раз, т. е. разделить на постоянную величину (k), и из частных вычислить среднюю, то онa окажется уменьшенной в такое же число раз, а поэтому, чтобы получить среднюю из вариантов нужно найденную среднюю умножить на ту же постоянную величину (k):

Доказательство.

Имеем частные от деления вариантов х на постоянную величину k, обозначенные х’:

Находим среднюю из

откуда

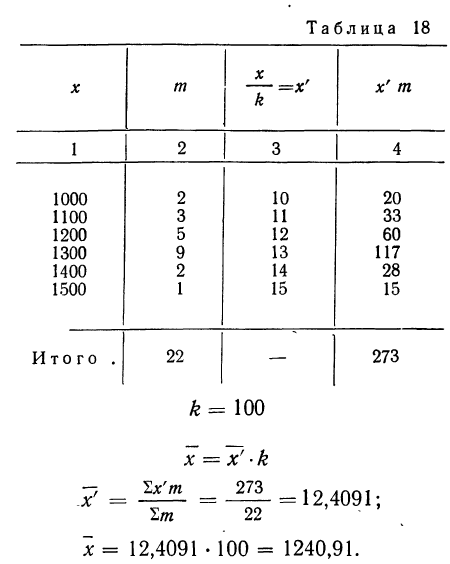
Пример 18.

Вычислить среднюю путем деления всех вариантов на 100 по следующим данным (колонки 1 и 2):

6) При вычислении средней вместо абсолютных значений весов (m) можно использовать относительные величины структуры (частости), т. е. удельные веса отдельных частот в общей сумме всех частот (см. § 4), или относительные величины координации, которые получаются путем отношения частот всех вариантов к одной из частот, принятой за единицу

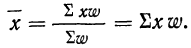
Если же удельные веса частот выражены в процентах, то

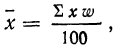
где 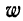— частость, т. е. доля частоты варианта в общей сумме частот.

Значит

Пример 19.

Вычислить средний размер детали по следующим данным (колонки 1 и 2):

Предварительно найдем относительные величины структуры (колонка 3), а затем вычислим средний размер детали, используя их в качестве весов: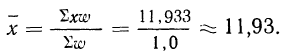

Если теперь вычислить средний размер детали, используя в качестве весов частоты, то получим: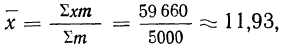

что согласуется с результатом, полученным ранее.

Для вычисления средней можно было использовать колонку 4 :

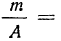
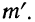
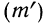
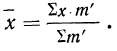
7) Если в частотах (m) имеется общий множитель (A), то его можно при вычислении средней не принимать во внимание т. е. взвешивание производить по сокращенным частотам Численное значение средней от замены частот (m) на сокращенные частоты не изменится

Доказательство.

Имеем:

Разделим частоты на общий множитель А, содержащийся в них:

Тогда

Пример 20.

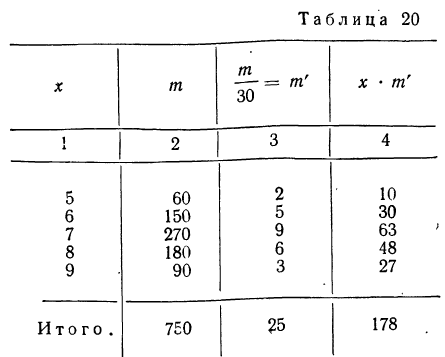
Вычислить среднюю по данным табл. 20 (колонки 1 и 2), произведя взвешивание вариантов по сокращенным весам.

Вычисляем среднюю по указанной формуле, предварительно сократив веса и заполнив колонки 3 и 4.

8) Общая средняя равна-.-взвешенной средней из частных средних: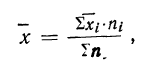

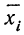
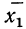
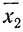
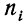
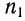
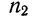
где — частные средние, т. е. средние для отдельных групп совокупности;

— средняя из вариантов первой группы;

— средняя из вариантов второй группы и т. д.;

— частоты отдельных групп;

— частота первой группы;

— частота второй группы и т. д.

Пусть имеются частные средние:

Найдем среднюю для всей совокупности:

Пример 21.

В трех, партиях продукции численностью 1000, 2000 и 500 единиц найден средний вес детали (в кг): 3,3; 3,1; 3,7. Вычислить средний вес детали во всех трех партиях

9) Сумма квадратов отклонений от средней меньше суммы квадратов отклонений от произвольной величины (В) на величину поправки С, равной произведению объема совокупности на квадрат разности между средней и данной произвольной величиной:

для случая невзвешенной средней или

для случая взвешенной средней.

Доказательство для случая невзвешенной средней.

Пользуясь свойствами сумм (см. стр. 11), производим преобразования:

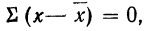
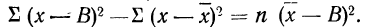
На основании второго свойства средней арифметической а поэтому

Пример 22.

По данным табл. 21 (колонки 1 и 2) убедиться в правильности указанных соотношений.

Вычисляем колонки 3, 4, 5, 6, 7, 8, 9 и находим:

Подставляя полученные результаты в формулу

имеем:

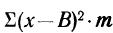
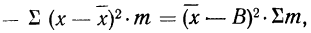
Метод отсчета от условного нуля

Упрощенное вычисление средней, состоящее в использовании ряда ее свойств, называется методом отсчета от условного нуля и предполагает:

Кроме того, в качестве весов используют сокращенные частоты 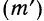или относительные величины (структуры или координации).

Формула исчисления средней методом отсчета от условного нуля:

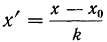
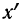
где , т. е. отклонение от начала отсчета делится на общий множитель, а исчисление средней из в зависимости от того, какими весами мы располагаем, производится по одной из следующих формул:

где 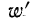— относительные величины координации (см. табл. 19).

Пример 23.

Вычислить средний вес зерен (на 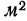) по данным колонок 1 и 2 табл. 22 (см. стр. 38), используя метод отсчета от условного нуля.

Используем формулу 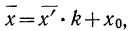предварительно заполнив колонки 3, 4, 5 и 6 табл. 22:

Метод стандартизации средних

Метод стандартизации средних наиболее разработан в статистике населения (демографической) и медицинской статистике, когда производится сравнение совокупностей с различными Структурами. Стандартизация достигается элиминированием (устранением) влияния различия в структурах совокупностей. Результат сравнения характеризует различие в средних при условии, что структура сравниваемых совокупностей одинакова.

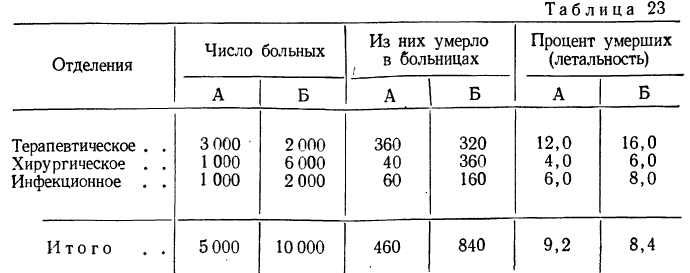
Рассмотрим применение метода стандартизации на примере из медицинской статистики. Имеются данные о двух больницах А и Б по отделениям и в целом.

Получается парадоксальное положение, при котором по больнице Б итоговая (общая) летальность (8,4%) ниже, чем в больнице А (9,2%), хотя по всем отделениям летальность в больнице Б выше (см. последние две колонки).

Причиной этого парадокса является отличие удельных весов разных отделений в больницах. Доля терапевтического отделения (по числу больных) с самой высокой летальностью составляет в больнице А 60%„ а в больнице Б — 20%, а доля хирургического отделения, с самой низкой летальностью, в больнице А — 20%, а в больнице Б — 60%.

Устраним влияние различия в структурах и стандартизуем распределение больных по отделениям. В качестве стандарта можно взять распределение больных по отделениям в любой больнице или привлечь данные о распределении больных нескольких других больниц. Возьмем за стандарт распределение больных в больнице А. Тогда по больнице А общая летальность (9,2%) останется без изменения. По больнице Б произведем пересчет.

Находим среднюю стандартизованную летальность больных больницы Б:

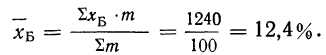
Таким образом, после стандартизации летальность в больнице Б оказалась значительно выше,, чем в больнице А: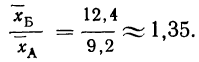

Следует иметь в виду, что полученное значение стандартизованной средней может служить только для сравнительных целей, абсолютное же ее значение принимать во внимание не следует.

Если за стандарт принять распределение больных в больнице Б, то получим следующую стандартизованную летальность для больницы А:

а отношение стандартизованных средних почти не изменится:

Мажорантность средних

Если вычислить различные типы средних для одного и того же вариационного ряда, то численные их значения будут отличаться друг от друга. При этом средние по своей величине расположатся в определенном порядке. Наименьшей из перечисленных средних окажется средняя гармоническая, затем геометрическая и т. д., наибольшей — средняя квадратическая. Порядок возрастания средних при этом определяется показателем степени z в формуле степенной средней и вытекает из «правила мажорантности».

Так,
при z= —1 получаем среднюю гармоническую,

при z= 0 »» геометрическую,

при z= 1 »» арифметическую,

при z= 2 »» квадратическую:

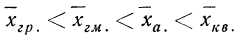
Подробное выяснение общего условия мажорантности впервые было произведено А. Я. Боярским, доказавшим, что если две средние должны удовлетворять соответственно уравнениям

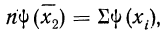
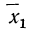
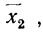
то первая из них мажорантна в отношении если при любом значении аргумента

Для степенной средней порядка z имеем: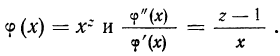

Это отношение для положительных значений с показателем x растет вместе с показателем z.

Пример 24.

Вычислить различные типы средних,по следующим данным (колонки 1 и 2) и убедиться в правильности порядка возрастания средних:

Заполняем колонки с 3-й по 8-ю и по соответствующим формулам исчисляем средние взвешенные:

Порядок средних определился в соответствии с правилом мажорантности:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник