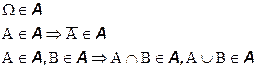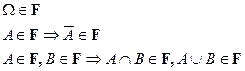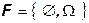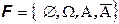Что такое сигма алгебра для чайников

Алгебра и сигма-алгебра

При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:

Алгебра событийAэто набор подмножеств пространства элементарных исходов для которого выполняются следующие условия:

и для любой счетной последовательности

Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.

Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.

Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.

Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств

Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.

Источник

Сигма-алгебра

σ-алгебра (си́гма-а́лгебра) — алгебра множеств, замкнутая относительно операции счётного объединения. Сигма-алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей.

Содержание

Определение

Семейство подмножеств множества называется σ-алгеброй, если оно удовлетворяет следующим свойствам:

Замечания

Связанные определения

Примеры

Полезное

Смотреть что такое «Сигма-алгебра» в других словарях:

Булева сигма-алгебра — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… … Википедия

Борелевская сигма-алгебра — это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (также она содержит и все замкнутые). Эти подмножества также называются Борелевыми. Если не оговорено противное, в качестве топологического… … Википедия

Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия

Алгебра (значения) — Алгебра раздел математики либо математическая структура специального вида (см. Алгебраическая система) Как раздел математики Абстрактная алгебра Алгебра логики раздел математической логики. Коммутативная алгебра Линейная алгебра… … Википедия

Алгебра множеств — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия

Сигма — У этого слова несколько значений: Сигма буква греческого алфавита. Сигма (язык) Стандартное отклонение в теории вероятностей. Сигма алгебра в теории множеств. «Сигма» чешский футбольный клуб. Sigma Corporation японский производитель… … Википедия

Σ-алгебра — (сигма алгебра) это алгебра множеств, замкнутая относительно операции счётного объединения. Сигма алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей. Содержание 1 Определение 2 Замечания 3 … Википедия

Борелевская алгебра — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… … Википедия

Измеримое пространство — σ алгебра (сигма алгебра) это алгебра множеств, замкнутая относительно операции счётного объединения. Сигма алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей. Содержание 1 Определение 2 Замечания 3 … Википедия

Источник

Зачем нам нужны сигма-алгебры для определения вероятностных пространств?

Может ли кто-нибудь объяснить простым языком, почему здание вероятности рухнет, если у нас не будет σ ‘ role=»presentation»> σ алгебры? Они просто вклиниваются посередине с этим невероятно каллиграфическим «F». Я верю, что они необходимы; Я вижу, что событие отличается от результата, но что было бы неправильно без σ ‘ role=»presentation»> σ алгебры?

Вопрос в том, в каком типе вероятностных задач определение вероятностного пространства, включающего σ ‘ role=»presentation»> σ алгебру, становится необходимостью?

Этот онлайн-документ на веб-сайте Дартмутского университета дает понятное объяснение на английском языке. Идея заключается в вращающемся указателе, вращающемся против часовой стрелки на окружности единицы периметра:

К первому пункту Сианя: когда вы говорите об алгебрах, вы спрашиваете об измеримых множествах, поэтому, к сожалению, любой ответ должен быть сосредоточен на теории меры. Я постараюсь довести это до конца нежно. σ ‘ role=»presentation»> σ

Теория вероятностей, допускающая все подмножества несчетных множеств, сломает математику

Но что, если область набора интересов не является четко определенной?

Хорошая новость: алгебры строго необходимы только для несчетных множеств σ ‘ role=»presentation»> σ

Поэтому на практике достаточно просто сделать это наблюдение достаточным для того, чтобы сделать наблюдение, в котором вы рассматриваете только измеримые по Лебегу множества, чтобы добиться прогресса в решении проблемы интересов.

Но подождите, что такое неизмеримый набор?

Боюсь, я могу только пролить немного света на это сам. Но парадокс Банаха-Тарского (иногда парадокс «солнца и гороха») может нам помочь:

Для заданного сплошного шара в трехмерном пространстве существует разложение шара на конечное число непересекающихся подмножеств, которые затем можно соединить по-разному, чтобы получить две идентичные копии исходного шара. Действительно, процесс сборки включает в себя только перемещение деталей и их вращение без изменения их формы. Однако сами кусочки являются не «твердыми телами» в обычном смысле, а бесконечным рассеянием точек. Реконструкция может работать всего с пятью частями.

Более сильная форма теоремы подразумевает, что при наличии любых двух «разумных» твердых объектов (таких как маленький шар и огромный шар) любой из них может быть повторно собран в другой. Об этом часто говорят неформально: «горох можно нарезать и снова собрать в Солнце» и называют «парадоксом гороха и солнца». 1

Чтобы разрешить этот парадокс, можно сделать одну из четырех уступок:

Источник

В теории вероятностей предполагается, что в опыте наблюдаются события, а не элементарные исходы. Это означает, что два описания опыта с одним и тем же пространством элементарных исходов, но разными сигма-алгебрами будут различны. Если в опыте с бросанием двух игральных костей определить пространство с 36 исходами (5 вариант), то тривиальная сигма-алгебра и наибольшая сигма–алгебра дают абсолютно разные описания опыта. Наблюдая события тривиальной сигма–алгебры мы не получаем никакой информации об значении элементарного исхода, наблюдая события второй точно знаем, какое из элементарных событий произошло. Любая другая сигма-алгебра дает частичную информацию об элементарных исходах. Например, сигма-алгебра

дает только информацию о том, совпадают ли значения на двух игральных костях.

Пересечение сигма-алгебр

Минимальная сигма-алгебра

Пусть D – некоторый набор случайных событий (набор любой мощности). Пересечение всех сигма-алгебр, содержаших этот набор, называется минимальная сигма-алгебра, порожденная набором D и обозначается

Полная группа событий

Конечно-аддитивная функция

называется конечно-аддитивной, если для любого конечного набора попарно несовместных событий

Счетно-аддитивная функция

Пусть F – алгебра или сигма-алгебра. Функция

называется счетно-аддитивной, если она конечно-аддитивна и для любого счетного набора попарно несовместных событий

Мера

Конечная мера

Мера называется конечной, если

Вероятность

С этого момента мы перестанем измерять вероятность в процентах и начнем измерять ее действительными числами от 0 до 1.

называют вероятностью события A

Вероятностное пространство

Вероятностное пространство это совокупность трех объектов – пространства элементарных исходов, сигма-алгебры событий и вероятности.

Это и есть математическая модель случайного явления или объекта.

Парадокс определения вероятностного пространства

Вернемся к исходной постановке задачи теории вероятностей. Нашей целью было построение математической модели случайного явления, которая помогла бы количественно оценить вероятности случайных событий. В то же время для построения вероятностного пространства необходимо задать вероятность, т.е. вроде бы именно то, что мы ищем (?).

Разрешение этого парадокса в том, что для полного определения вероятности как функции на всех элементах F,обычно достаточно задать ее на лишь на некоторых событиях из F, вероятность которых нам легко определить, а затем, пользуясь ее счетной аддитивностью, вычислить на любом элементе F.

Независимые события

Важным понятием теории вероятностей является независимость.

События A и B называются независимыми, если

т.е. вероятность одновременного осуществления этих событий равна произведению их вероятностей.

Попарно

События в счетном или конечном наборе называются независимыми попарно, если любая пара из них является парой независимых событий

В совокупности

Ясно, что независимые в совокупности события независимы и попарно. Обратное неверно.

Условная вероятность

Условной вероятностью события A при условии, что произошло событие B называется величина

Условную вероятность пока определим лишь для событий B, вероятность которых не равна нулю.

Если события A и B независимы, то

Свойства и теоремы

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Зачем нам нужны сигма-алгебры для определения вероятностных пространств?

В вероятностном пространстве существует множество-носитель, элементами которого являются исходы вашего вероятностного опыта. Любой опыт заканчивается каким-то исходом, который содержится в основном множестве носителе. Событиями в вероятностном пространстве служат подмножества основного множества. То есть событие — это совокупность исходов, которые считаются благоприятными для этого события. Обычно вы имеете дело не с одним событием, а сразу со множеством разных событий, возможно даже бесконечным множеством разных событий. В теории вероятностей часто изучают взаимосвязь между событиями, их независимость или зависимость, их одновременное выполнение. Возникают естественные операции над событиями, такие как пересечение событий (одновременное выполнение), объединение событий (что хотя бы одно произойдет), а также интересует вопрос вычисления вероятностей таких производных событий. Разумеется, удобно, чтобы пересечение/объединение событий, как пересечение/объединение множеств, само являлось событием в нашем вероятностном пространстве. Причем неплохо было бы, чтобы можно было рассуждать о пересечении/объединении не только конечного, но и даже счетного числа различных событий (подмножеств). Вот мы и подошли к сигма-алгебре, которая ровно это и требует.

Семейство подмножеств S множества X называется σ-алгеброй, если объединение или пересечение счётного подсемейства принадлежит S. Кроме того, любое подмножество A лежит в семействе вместе со своим дополнением X\A (противоположное событие с вероятностью 1-p, где p — вероятность A), а также все множество X входит в S (достоверное событие с вероятностью 1).

Источник