Что такое сигма дельта ацп
Аналого-цифровое преобразование для начинающих
В этой статье рассмотрены основные вопросы, касающиеся принципа действия АЦП различных типов. При этом некоторые важные теоретические выкладки, касающиеся математического описания аналого-цифрового преобразования остались за рамками статьи, но приведены ссылки, по которым заинтересованный читатель сможет найти более глубокое рассмотрение теоретических аспектов работы АЦП. Таким образом, статья касается в большей степени понимания общих принципов функционирования АЦП, чем теоретического анализа их работы.

В качестве отправной точки дадим определение аналого-цифровому преобразованию. Аналого-цифровое преобразование – это процесс преобразования входной физической величины в ее числовое представление. Аналого-цифровой преобразователь – устройство, выполняющее такое преобразование. Формально, входной величиной АЦП может быть любая физическая величина – напряжение, ток, сопротивление, емкость, частота следования импульсов, угол поворота вала и т.п. Однако, для определенности, в дальнейшем под АЦП мы будем понимать исключительно преобразователи напряжение-код.
Понятие аналого-цифрового преобразования тесно связано с понятием измерения. Под измерением понимается процесс сравнения измеряемой величины с некоторым эталоном, при аналого-цифровом преобразовании происходит сравнение входной величины с некоторой опорной величиной (как правило, с опорным напряжением). Таким образом, аналого-цифровое преобразование может рассматриваться как измерение значения входного сигнала, и к нему применимы все понятия метрологии, такие, как погрешности измерения.
Основные характеристики АЦП
АЦП имеет множество характеристик, из которых основными можно назвать частоту преобразования и разрядность. Частота преобразования обычно выражается в отсчетах в секунду (samples per second, SPS), разрядность – в битах. Современные АЦП могут иметь разрядность до 24 бит и скорость преобразования до единиц GSPS (конечно, не одновременно). Чем выше скорость и разрядность, тем труднее получить требуемые характеристики, тем дороже и сложнее преобразователь. Скорость преобразования и разрядность связаны друг с другом определенным образом, и мы можем повысить эффективную разрядность преобразования, пожертвовав скоростью.
Существует множество типов АЦП, однако в рамках данной статьи мы ограничимся рассмотрением только следующих типов:
Наибольшим быстродействием и самой низкой разрядностью обладают АЦП прямого (параллельного) преобразования. Например, АЦП параллельного преобразования TLC5540 фирмы Texas Instruments обладает быстродействием 40MSPS при разрядности всего 8 бит. АЦП данного типа могут иметь скорость преобразования до 1 GSPS. Здесь можно отметить, что еще большим быстродействием обладают конвейерные АЦП (pipelined ADC), однако они являются комбинацией нескольких АЦП с меньшим быстродействием и их рассмотрение выходит за рамки данной статьи.
Среднюю нишу в ряду разрядность-скорость занимают АЦП последовательного приближения. Типичными значениями является разрядность 12-18 бит при частоте преобразования 100KSPS-1MSPS.
Наибольшей точности достигают сигма-дельта АЦП, имеющие разрядность до 24 бит включительно и скорость от единиц SPS до единиц KSPS.
Еще одним типом АЦП, который находил применение в недавнем прошлом, является интегрирующий АЦП. Интегрирующие АЦП в настоящее время практически полностью вытеснены другими типами АЦП, но могут встретиться в старых измерительных приборах.
АЦП прямого преобразования
АЦП прямого преобразования получили широкое распространение в 1960-1970 годах, и стали производиться в виде интегральных схем в 1980-х. Они часто используются в составе «конвейерных» АЦП (в данной статье не рассматриваются), и имеют разрядность 6-8 бит при скорости до 1 GSPS.
Архитектура АЦП прямого преобразования изображена на рис. 1
Рис. 1. Структурная схема АЦП прямого преобразования
Принцип действия АЦП предельно прост: входной сигнал поступает одновременно на все «плюсовые» входы компараторов, а на «минусовые» подается ряд напряжений, получаемых из опорного путем деления резисторами R. Для схемы на рис. 1 этот ряд будет таким: (1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16) Uref, где Uref – опорное напряжение АЦП.
Пусть на вход АЦП подается напряжение, равное 1/2 Uref. Тогда сработают первые 4 компаратора (если считать снизу), и на их выходах появятся логические единицы. Приоритетный шифратор (priority encoder) сформирует из «столбца» единиц двоичный код, который фиксируется выходным регистром.
Теперь становятся понятны достоинства и недостатки такого преобразователя. Все компараторы работают параллельно, время задержки схемы равно времени задержки в одном компараторе плюс время задержки в шифраторе. Компаратор и шифратор можно сделать очень быстрыми, в итоге вся схема имеет очень высокое быстродействие.
Но для получения N разрядов нужно 2^N компараторов (и сложность шифратора тоже растет как 2^N). Схема на рис. 1. содержит 8 компараторов и имеет 3 разряда, для получения 8 разрядов нужно уже 256 компараторов, для 10 разрядов – 1024 компаратора, для 24-битного АЦП их понадобилось бы свыше 16 млн. Однако таких высот техника еще не достигла.
АЦП последовательного приближения
АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь. Подробнее о задаче Фибоначчи можно прочитать, например, здесь: http://www.goldenmuseum.com/2015AMT_rus.html.
Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины входного напряжения с рядом величин, генерируемых следующим образом:
1. на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref).
2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref).
3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата.
Рис. 2. Структурная схема АЦП последовательного приближения.
Таким образом, АЦП последовательного приближения состоит из следующих узлов:
1. Компаратор. Он сравнивает входную величину и текущее значение «весового» напряжения (на рис. 2. обозначен треугольником).
2. Цифро-аналоговый преобразователь (Digital to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода.
3. Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП.
4. Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства.
Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767).
И, наконец, самый интересный тип АЦП – сигма-дельта АЦП, иногда называемый в литературе АЦП с балансировкой заряда. Структурная схема сигма-дельта АЦП приведена на рис. 3.
Рис.3. Структурная схема сигма-дельта АЦП.
Принцип действия данного АЦП несколько более сложен, чем у других типов АЦП. Его суть в том, что входное напряжение сравнивается со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжение (рис. 4). Результатом работы данной схемы является поток нулей и единиц на выходе компаратора, который затем пропускается через цифровой ФНЧ, в результате получается N-битный результат. ФНЧ на рис. 3. Объединен с «дециматором», устройством, снижающим частоту следования отсчетов путем их «прореживания».
Рис. 4. Сигма-дельта АЦП как следящая система
Ради строгости изложения, нужно сказать, что на рис. 3 изображена структурная схема сигма-дельта АЦП первого порядка. Сигма-дельта АЦП второго порядка имеет два интегратора и две петли обратной связи, но здесь рассматриваться не будет. Интересующиеся данной темой могут обратиться к [3].
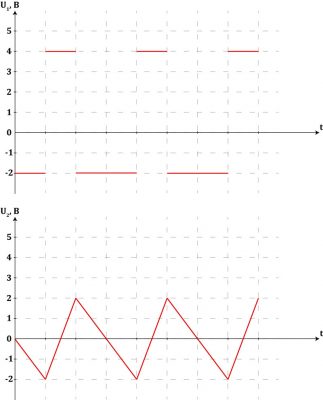
На рис. 5 показаны сигналы в АЦП при нулевом уровне на входе (сверху) и при уровне Vref/2 (снизу).
Рис. 5. Сигналы в АЦП при разных уровнях сигнала на входе.
Более наглядно работу сигма-дельта АЦП демонстрирует небольшая программа, находящаяся тут: http://designtools.analog.com/dt/sdtutorial/sdtutorial.html.
Теперь, не углубляясь в сложный математический анализ, попробуем понять, почему сигма-дельта АЦП обладают очень низким уровнем собственных шумов.
Рассмотрим структурную схему сигма-дельта модулятора, изображенную на рис. 3, и представим ее в таком виде (рис. 6):
Рис. 6. Структурная схема сигма-дельта модулятора
Здесь компаратор представлен как сумматор, который суммирует непрерывный полезный сигнал и шум квантования.
Пусть интегратор имеет передаточную функцию 1/s. Тогда, представив полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:
То есть, фактически сигма-дельта модулятор является фильтром низких частот (1/(s+1)) для полезного сигнала, и фильтром высоких частот (s/(s+1)) для шума, причем оба фильтра имеют одинаковую частоту среза. Шум, сосредоточенный в высокочастотной области спектра, легко удаляется цифровым ФНЧ, который стоит после модулятора.
Рис. 7. Явление «вытеснения» шума в высокочастотную часть спектра
Однако следует понимать, что это чрезвычайно упрощенное объяснение явления вытеснения шума (noise shaping) в сигма-дельта АЦП.
Итак, основным достоинством сигма-дельта АЦП является высокая точность, обусловленная крайне низким уровнем собственного шума. Однако для достижения высокой точности нужно, чтобы частота среза цифрового фильтра была как можно ниже, во много раз меньше частоты работы сигма-дельта модулятора. Поэтому сигма-дельта АЦП имеют низкую скорость преобразования.
Они могут использоваться в аудиотехнике, однако основное применение находят в промышленной автоматике для преобразования сигналов датчиков, в измерительных приборах, и в других приложениях, где требуется высокая точность. но не требуется высокой скорости.
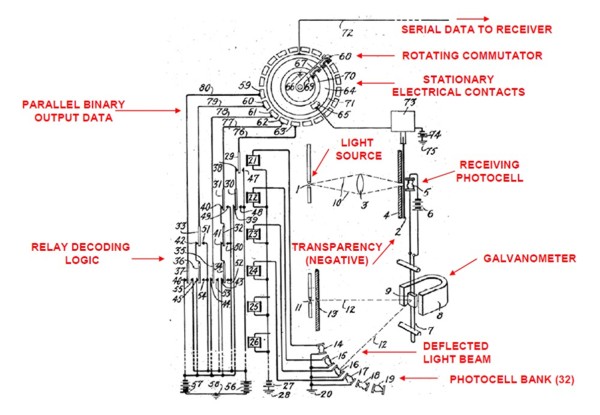
Самым старым упоминанием АЦП в истории является, вероятно, патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Изображенное в патенте устройство фактически является 5-битным АЦП прямого преобразования.
Рис. 8. Первый патент на АЦП
Рис. 9. АЦП прямого преобразования (1975 г.)
Устройство, изображенное на рисунке, представляет собой АЦП прямого преобразования MOD-4100 производства Computer Labs, 1975 года выпуска, собранный на основе дискретных компараторов. Компараторов 16 штук (они расположены полукругом, для того, чтобы уравнять задержку распространения сигнала до каждого компаратора), следовательно, АЦП имеет разрядность всего 4 бита. Скорость преобразования 100 MSPS, потребляемая мощность 14 ватт.
На следующем рисунке изображена продвинутая версия АЦП прямого преобразования.
Рис. 10. АЦП прямого преобразования (1970 г.)
Устройство VHS-630 1970 года выпуска, произведенное фирмой Computer Labs, содержало 64 компаратора, имело разрядность 6 бит, скорость 30MSPS и потребляло 100 ватт (версия 1975 года VHS-675 имела скорость 75 MSPS и потребление 130 ватт).
Разнообразие аналогово-цифровых преобразователей вырождается?
Первый АЦП
Самым первым упоминанием АЦП в истории является патент США 1 608 527 под названием «Facsimile Telegraph System», который был подан 20 июля 1921 года Полом М. Рейни, работником компании Western Electric. Патент был получен спустя 6 лет, 30 ноября 1926 года.
Рисунок 1 – Патент «Facsimile Telegraph System»
Изображенное в патенте устройство фактически является 5-битным АЦП прямого преобразования (flash ADC, direct-conversion ADC). Принцип действия полностью параллельного АЦП прямого преобразования заключается в том, что все параллельные компараторы с напряжением сравнения меньшим, чем уровень входного сигнала переключаются в «1», а все параллельные компараторы с напряжением сравнения бо́льшим, чем уровень входного сигнала остаются в состоянии «0». Шифратор перекодирует полученный двоично кодированный унарный код (Binary Coded Unary, BCU) в код для передачи дальнейшим устройствам.
Типы существующих АЦП
АЦП имеет множество характеристик, которые условно можно разделить на статические:
Скорость преобразования и разрядность связаны друг с другом определенным образом, и мы можем повысить эффективную разрядность преобразования, пожертвовав скоростью.
На рисунке 2 показан график зависимости разрядности различных типов АЦП от частоты преобразования.
Рисунок 2 – График зависимости разрядности различных типов АЦП от частоты преобразования
Наибольшим быстродействием и самой низкой разрядностью обладают АЦП прямого (параллельного) преобразования. Например, АЦП параллельного преобразования TLC5540 фирмы Texas Instruments обладает быстродействием 40 MSPS при разрядности всего 8 бит. АЦП данного типа могут иметь скорость преобразования до 1 GSPS. Среднюю нишу в ряду разрядность-скорость занимают АЦП последовательного приближения. Типичными значениями является разрядность 12-18 бит при частоте преобразования 100 kSPS — 1 MSPS. Наибольшей точности достигают сигма-дельта АЦП, имеющие разрядность до 24 бит включительно и скорость от единиц SPS до десятков kSPS. Интегрирующие АЦП в настоящее время практически полностью вытеснены другими типами АЦП, но могут встретиться в измерительных приборах.
Сигма-дельта АЦП
На хабре была статья 2011 года, где упоминались разные типы АЦП, но в данной статье смысл совсем другой.
Структура любого сигма-дельта АЦП содержит сигма-дельта модулятор, который преобразует входной аналоговый сигнал в последовательность нулей и единиц, и цифровой фильтр-дециматор. Эта последовательность нулей и единиц в иностранной литературе называется PDM (pulse density modulation), что принципиально отличает ее от ШИМ (широтно импульсной модуляции).
Рисунок 3 структура сигма-дельта АЦП
Входной сигнал поступает на блок вычитания полученного битового кода, далее на интегратор, компаратор и триггер (элемент задержки по времени), выход триггера — последовательность битового кода PDM. Данная последовательность поступает на усредняющий ФНЧ, дециматор, и на выходе получается оцифрованный сигнал высокой разрядности (разрядность повышается внутри фильтра). Надо заметить, что частота следования нулей и единиц в потоке PDM должна быть существенно выше, чем частота построения выходного кода высокой разрядности. В простейшем случае для получения 8-битного АЦП необходимо повышение частоты PDM в 256 раз. Это неудобно и нерационально.
Поэтому сигма-дельта модуляторы собирают последовательно в количестве 2..3..7 штук, возникает эффект модуляции шума, перенос энергии шума на высокие частоты, и как следствие в рабочей низкочастотной области шумов оказывается меньше. Это позволяет получить «эффективную» разрядность существенно выше, что у PDM первого порядка, как показано на рисунке 4.
Рисунок 4 Формирование спектра шума сигма-дельта модуляторов разного порядка
Таким образом, при повышении частоты дискретизации в 64 раза и использовании сигма-дельта модулятора 4 порядка можно получить разрядность 12 бит вместо 6. При повышении порядка до 7 и той же частоте дискретизации разрядность можно поднять уже до 16. Таким образом, оказывается возможным создавать сигма-дельта АЦП не только до единиц-десятков kSPS, но и существенно больше. Например, если производить цифровую фильтрацию PDM в ПЛИС Xilinx на частоте 400 МГц (что вполне реализуемо с использованием аппаратных умножителей и дифференциальных входов), коэффициенте передискретизации 64 можно получить 16-битный АЦП на частоте 6.250 MSPS. При меньшей разрядности можно увеличить частоту дискретизации. Данный тип АЦП можно использовать для синхронной обработки большого числа АЦП, особенно если всю цифровую обработку всех потоков PDM поместить внутри одной ПЛИС.
Классический рисунок областей применения различных АЦП можно изменить так:
Рисунок 5 Современное состояние различных типов АЦП
Сигма-дельта АЦП могут заменить собой практически все другие типы АЦП кроме наиболее быстродействующих параллельных. И по большинству параметров окажутся лучше старых аналогов других типов.
Принцип работы сигма-дельта АЦП.
И снова здравствуйте! 🙂 В продолжение моей предыдущей статьи хочу опубликовать и еще одну по смежной теме. А именно речь пойдет о структурной схеме, устройстве и принципе работы сигма-дельта модулятора. А на модуляторе уже базируются сигма-дельта аналого-цифровые преобразователи (АЦП). Постараюсь больше внимания уделить не стандартным общим словам, а конкретным примерам, чтобы лучше описать именно принцип работы.
Сигма-дельта модулятор.
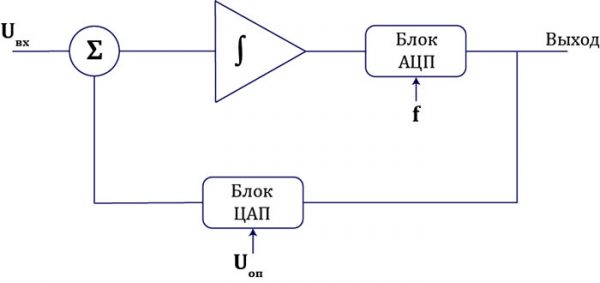
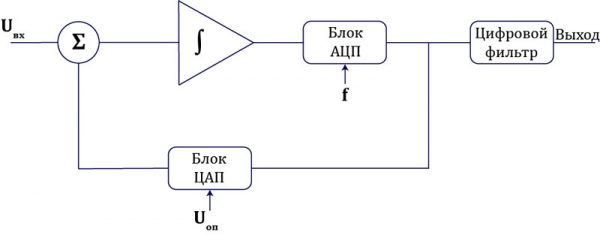
Структурная схема модулятора выглядит вот так:
Ключевые элементы схемы – сумматор (∑) и интегратор (∫). Кроме того, в схему входит блок АЦП, который преобразует аналоговое напряжение на выходе интегратора в биты. Эти биты идут как на выход, так и в цепь обратной связи. А в цепи обратной связи находится ЦАП, который на входе имеет эти же биты, а также определенное опорное напряжение. Итогом работы блока ЦАП будет аналоговое напряжение, которое поступает на сумматор. Пока это еще только теоретическая часть, из которой суть устройства далеко не очевидна, но обязательно рассмотрим и практический пример 🙂
Сигма-дельта АЦП.
Дополнив модулятор блоком цифрового фильтра, получаем схему сигма-дельта АЦП:
И уже на выходе данного фильтра мы получим тот цифровой код, который нам и нужен. Если представить сигма-дельта АЦП в виде черного ящика, то на входе мы имеем аналоговое напряжение Uвх а на выходе цифровой код. При изменении Uвх меняется и этот код.
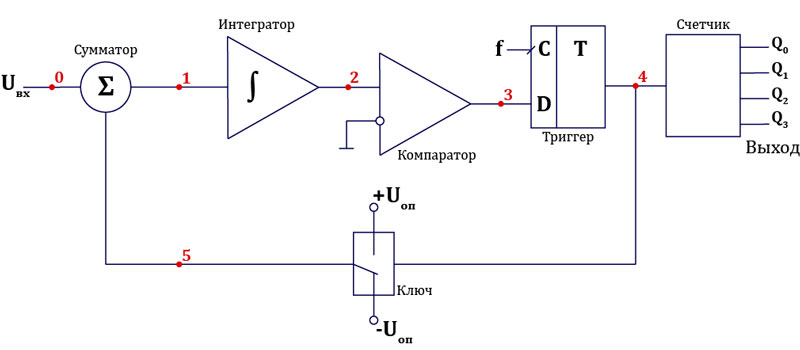
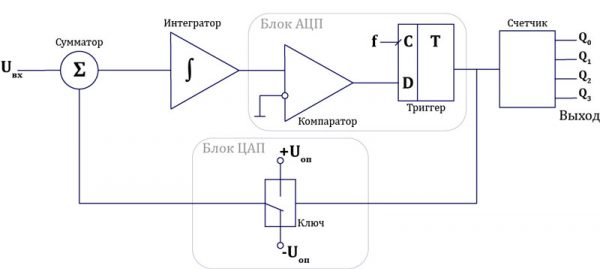
Теория теорией, но из нее принцип работы вынести не так просто. Поэтому попробуем разобрать небольшой пример реальной работы. И для этого рассмотрим АЦП первого порядка. Вообще такие АЦП бывают разных порядков – отличие в количестве сумматоров и интеграторов. Так преобразователь 5-го порядка содержит 5 сумматоров и 5 интеграторов. Но нас пока интересует первый порядок. Схема выглядит так:
Давайте соотнесем ее с общей схемой из начала статьи. Сумматор и интегратор остаются собой и на этой схеме, ключевые узлы, как ни крути. Блок АЦП первой схемы здесь состоит из компаратора и D-триггера с динамической синхронизацией. А блок ЦАП представляет из себя простой ключ. Работает он так:
| Вход, бит | Выход, В |
|---|---|
| 0 | Uоп |
| 1 | − Uоп |
В качестве же цифрового фильтра может быть использован 4-разрядный двоичный счетчик. Суть работы этого счетчика заключается в подсчете количества единиц на входе и выдаче на выходы цифрового кода, который соответствует этому количеству:
| Кол-во единиц | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
И далее аналогично до числа 15, поскольку счетчик 4-х разрядный. Для 4-х разрядов максимальный код на выходе равен 1111 (0x0F), что соответствует 15-ти. Получаем, что если на входе счетчика всегда нулевой уровень, то на выходах:
| Кол-во единиц | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
Если на входе всегда «1», то на выходах:
| Кол-во единиц | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 15 | 1 | 1 | 1 | 1 |
Аналогично для промежуточных значений на входе. И вот теперь самое интересное, подадим на вход АЦП напряжение и посмотрим, какие будут сигналы в разных частях схемы!
Принцип работы.
Пусть опорное напряжение равно 3В, а на входе сигма-дельта АЦП будет 2В: U0 = 2В, Uоп = 3В.
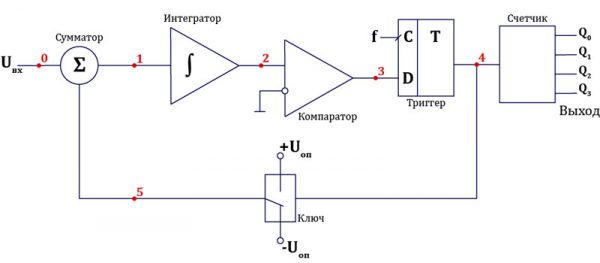
Схема будет менять свое состояние в соответствии с импульсами тактового сигнала на входе C триггера. Поэтому нам нужно разбить временную шкалу на части, которые равны периоду этого сигнала и определить, какие будут значения напряжений в разных точных схемы на разных интервалах.
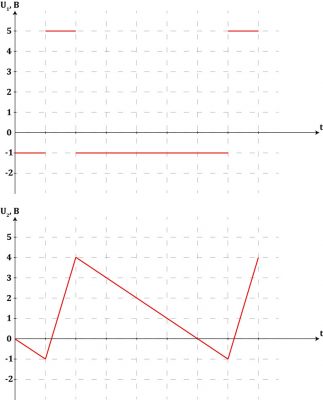
Интервал 1.
В течении интервала 1 (также будет и для других интервалов) на входе интегратора постоянное напряжение. А значит на выходе интегратора будет «пила», наклон которой определяется величиной входного сигнала. В данном случае на входе U1 = − 1В, значит напряжение на выходе интегратора изменится на − 1В за этот промежуток времени:
Вот и второй интервал разобран. Составим таблицу и графики для этих и некоторого количества последующих отрезков:
| № | U0 | U1 | U2 | Точка 3 | Точка 4 (Выход) |
| 1 | 2В | − 1В | − 1В | 0 | 0 |
| 2 | 2В | 5В | 4В | 1 | 1 |
| 3 | 2В | − 1В | 3В | 1 | 1 |
| 4 | 2В | − 1В | 2В | 1 | 1 |
| 5 | 2В | − 1В | 1В | 1 | 1 |
| 6 | 2В | − 1В | 0В | 1 | 1 |
| 7 | 2В | − 1В | − 1В | 0 | 0 |
| 8 | 2В | 5В | 4В | 1 | 1 |
Здесь начиная с 7-го шага идет повторение всех процессов, поэтому мы легко можем продолжить ряд выходных значений. Для 15-ти интервалов получим:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
А если бы на вход приходил 1В, то результат был бы такой:
| № | U0 | U1 | U2 | Точка 3 | Точка 4 (Выход) |
|---|---|---|---|---|---|
| 1 | 1В | − 2В | − 2В | 0 | 0 |
| 2 | 1В | 4В | 2В | 1 | 1 |
| 3 | 1В | − 2В | 0В | 1 | 1 |
| 4 | 1В | − 2В | − 2В | 0 | 0 |
| 5 | 1В | − 4В | 2В | 1 | 1 |
| 6 | 1В | − 2В | 0В | 1 | 1 |
| 7 | 1В | − 2В | − 2В | 0 | 0 |
| 8 | 1В | 4В | 2В | 1 | 1 |
В результате также имеем последовательность битов:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Но это не совсем то, что нам требуется, поэтому в схеме присутствует еще и двоичный счетчик.
Счетчик подсчитывает количество единиц в подаваемой на его вход последовательности битов. При этом для 4-х разрядного счетчика максимальное количество подсчитанных единиц равно 15-ти. Потому что 15 единиц – это код 1111 (все четыре разряда = 1), после этого счетчик переполняется.
Давайте составим таблицу с полученными результатами для рассмотренных значений входного напряжения. При этом нас интересует период, равный 15-ти интервалам:
| Uвх | Кол-во единиц на входе счетчика | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|---|
| 2В | 12 | 1 | 1 | 0 | 0 |
| 1В | 10 | 1 | 0 | 1 | 0 |
Вот такой результат дает наша схема АЦП. Теперь можем проверить полученный на выходе цифровой код. Для 2В на входе на выходе счетчика мы получили код – 1100 (12 в десятичной системе счисления). При этом мы точно знаем, что при напряжении 3В на входе (равно опорному напряжению) на выходе модулятора у нас будут одни единицы. А на выходе счетчика мы получим «максимум», то есть код 1111 (15 единиц). А если на входе − 3В, то на выходе модулятора сплошные нули, значит на выходе счетчика – 0000 (0). Опираясь на эти точки — (3, 15) и ( − 3, 0) — мы можем вывести формулу для расчета аналогового напряжения из цифрового кода:
U = (выход счетчика) / 15 * (3 + 3) − 3 = (выход счетчика) / 15 * 6 − 3
А теперь возьмем полученный нами код с выхода счетчика (1101) и рассчитаем для него аналоговое значение напряжения: U = 12 / 15 * 6 − 3 = 1.8В. Для второго полученного значения (1010): U = 10 / 15 * 6 − 3 = 1В
Здесь мы не попали точно в значение 2В из-за того, что накопили значения всего лишь для 15-ти интервалов. Поэтому шаг между соседними значениями напряжений достаточно велик. Например, для выходного кода 1101 (13), получаем значение U = 2.2В. То есть соседние значения равны 1.8В и 2.2В, и разность между ними значительна.
На этом моя статья подходит к концу, всем спасибо за прочтение, надеюсь было познавательно 🙂