Что такое симметричная монета в математике
Часто для принятия единственного решения подкидывают монетку, ожидая увидеть птицу или цифру. В редких случаях монета упадет на ребро, ставя «решающего» в тупик.
Мало кто задумывается, что использование монеты, этакого способа «да/нет», применяется даже в математических экспериментах, а конкретно в теории вероятности. Только в этом случае используется понятие симметричной монеты, иногда называемой честной или математической. Это значит, что плотность одинакова по всей монете, а орел или решка могут выпасть с одинаковой долей вероятности. Кроме ставших привычными названий сторон у такой монеты больше нет признаков. Ни веса, ни цвета, ни размеров. Такая монета может выдать лишь два результата – реверс либо аверс, никаких «встать на ребро» в теории вероятности нет.
Все в мире вероятно
Теория вероятности – целая область, которая до сих пор пытается подчинить себе случай и рассчитать все варианты возможных исходов событий. Благодаря формулам и многочисленным эмпирическим способам эта наука дает судить о разумности ожидания. Если опираться на смысл сказанного профессором П. Лапласом (он внес важный вклад в развитие теории), то суть всех действий по теории вероятности – это попытка свести к вычислениям действие здравого смысла.
Слово «вероятно» напрямую относится к данной науке. Используется понятие «предположение», которое означает: возможно, произойдет какое-то событие. Если приблизиться именно к математике, то самый яркий пример – подбрасывание монетки. И тогда можно предполагать: в случайном эксперименте симметричную монету бросают 100 раз. Вероятно, что герб окажется сверху – от 45 до 55 раз. Уже потом предположение начинает подтверждаться или доказываться расчетами.
Расчеты против интуиции
Есть ситуации, когда интуицию еще сложнее противопоставить математическим расчетам. Невозможно предугадать или прочувствовать все варианты, если монет еще больше. В дело вводятся математические инструменты, связанные с комбинаторным анализом.
Пример для разбора
В случайном эксперименте симметричную монету подбрасывают три раза. Нужно вычислить вероятность выпадения решки во всех трех бросках.
Расчеты. Решка должна выпасть в 100% случаях эксперимента (3 раза), это один из 8 вариантов-комбинаций: три орла, два орла и решка и т.д. Значит, вычисление вероятности делается через деление 100% на общее число вариантов. То есть 1/8. Получаем ответ 0,125.
Задач для симметричной монеты приводится предостаточно. Но в теории вероятности есть примеры, которые заинтересуют даже людей, далеких от математики.
Спящая красавица
Один из парадоксов, авторство которого приписывается А. Элга, имеет «сказочное» название. Это очень хорошо отражает суть парадокса. Это задача, которая имеет несколько ответов, и каждый из них по-своему правильный. Пример явственно доказывает, насколько легко можно оперировать результатами, используя наиболее выгодный результат.
Спящую красавицу (героиню эксперимента) усыпляют снотворным через укол. Во время этого подкидывается симметричная монета. При выпадении стороны с орлом героиню будят, заканчивая эксперимент. При результате с решкой красавицу будят, после чего вновь усыпляют, чтобы разбудить на следующий день опыта. При этом красавица забывает о том, что она была разбужена, хотя условия эксперимента ей известны, не считая информации, в каком дне она проснулась. Далее – самый интересный вопрос, конкретно для разбуженной красавицы: «Вычислить вероятность выпадения стороны с решкой».
В этом парадоксальном примере есть два решения.
В первом случае без должной информации о побудках и итогах выпадения монет. Поскольку участвует симметричная монета, то получается ровно 50%.
Второе решение: для точных данных опыт проводится 1000 раз. Получается, что красавица была разбужена 500 раз, если был орел, и 1000 при решке. (Ведь при исходе с решкой героиню спрашивали два раза). Соответственно, вероятность составляет 2/3.
Жизненно
Подобное манипулирование данными в статистике встречается в жизни. Например, информация о доле пенсионеров в общественном транспорте. По информации, 40% поездок совершаются пенсионерами. Но ведь по факту пенсионеры не составляют 0,4 от всего населения. Объясняется это тем, что люди на пенсии более активно пользуются услугами транспорта. Реально количество пенсионеров регистрируется в пределах 18-20%. Если проводить учет только самой последней поездки пассажира без учета предыдущих, то процент пенсионеров в общем пассажиропотоке будет в районе 20%. Если сохранять все данные – то все 40%. Все зависит от субъекта, использующего эти данные. Маркетологам нужна первая цифра реальных показов их рекламы целевой аудитории, транспортников интересует общая цифра.
Примечательно, что из математических раскладов что-то все же просочилось в реальную жизнь. Именно симметричная монета стала использоваться для решения споров благодаря своей честной натуре и отсутствию каких-либо признаков пристрастности. Например, спортивные арбитры подкидывают ее, когда надо определить, кому из участников достанется первый ход.
В случайном эксперименте симметричную монету бросают.
Решение задачи с симметричной монетой
В случайном эксперименте симметричную монету бросают один раз
Здесь всё просто. Выпадет либо орёл, либо решка. То есть, имеем два возможных исхода, один из которых нас удовлетворяет
В случайном эксперименте симметричную монету бросают дважды
За два броска могут выпасть:
Итак, возможны всего четыре варианта. Задачи с более, чем одним броском, проще всего решать составлением таблицы возможных вариантов. Для простоты, обозначим орла цифрой «0», а решку цифрой «1».
Тогда таблица возможных исходов будет выглядеть так:
В случайном эксперименте симметричную монету бросают трижды
Составляем таблицу вариантов:
000
001
010
011
100
101
110
111
Вероятность того, что орёл в трёх бросках выпадет дважды тоже равна 3/8=37,5%, то есть абсолютно такая же.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 1/8=12,5%.
В случайном эксперименте симметричную монету бросают четырежды
Составляем таблицу вариантов:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Вероятность того, что орёл в трёх бросках выпадет дважды равна 6/8=75%.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 4/8=50%.
Теория вероятностей не так проста как кажется
Что нужно знать о теории вероятностей?
Автор — доцент института религиозных исследований и критической оценки Австралийского католического университета в Мельбурне. Его работы опубликованы в Journal of Philosophy и др.
Азартный игрок, физик-теоретик и присяжный рассуждают о теории вероятностей: какова вероятность выигрыша, радиоактивного распада и виновности подсудимого. Но, несмотря на повсеместность подобных рассуждений, эксперты спорят о самом существовании вероятностей. Это приводит к разногласиям о методах рассуждения: нужно учесть вероятность разногласий о способности когнитивных искажений усугублять, например, к игнорированию доказательств, противоречащих нашим убеждениям. Таким образом, понимание теории вероятностей может помочь нам рассуждать лучше.
Три популярные теории рассматривают вероятности c точки зрения частоты повторения, предрасположенности и степени уверенности. Допустим, я скажу вам, что если вы подбросите монетку, то с вероятностью в 50% выпадет «орёл». Речь в этих теориях идет соответственно о частоте повторения, с которой выпадает «орел»; физических свойствах монеты и тенденции к выпадению «орла»;
ВЕРОЯТНОСТЬ ВЫПАДЕНИЯ «ОРЛА» ПРИ ПЕРВОМ БРОСКЕ СОСТАВЛЯЕТ 75%.
Но у каждой из вышеописанных теорий есть небольшие проблемы. Рассмотрим следующий случай:
Адам подбрасывает симметричную монету*, которая становится невидимой после четвертого броска. Друзья Адама Бет, Чарльз и Дэйв сидят рядом, но с завязанными глазами. После четвертого броска Бет говорит: «вероятность того, что в первый раз выпал «орел» составляет 50%».
Затем Адам говорит друзьям, что «орел» выпал три раза из четырех. Чарльз считает, что вероятность выпадения «орла» при первом броске составляет 75%.
Несмотря на то, что Дэйв владеет той же информацией, что и Чарльз, он говорит: «я не согласен. Вероятность того, что при первом броске выпал «орел» составляет 60%».
*Симметричная монета — математическая монета, используемая в теории вероятностей, лишена многих качеств настоящей монеты. У математической монеты нет цвета, размера, веса и достоинства. Монета с точки зрения теории вероятностей имеет только две стороны, одна из которых называется «орел», а другая —«решка». Монету бросают, и она падает одной из сторон вверх. Никакие другие свойства математической монете не присущи — прим. переводчика.
Частота повторения не соответствует утверждению Бет. «Орел» выпал с частотой три из четырех, но подбросить монету снова нельзя. Кажется, Бет права: вероятность выпадения «орла» при первом броске составляет 50%.
В то же самое время, Чарльз говорил о тенденции к выпадению «орла». Поскольку это симметричная монета, и «орел» и «решка» могут выпасть с одинаковой вероятностью. Кажется, Чарльз оказался прав заявив, что вероятность выпадения «орла» при первом броске составляет 75%. Степень уверенности имеет смысл в двух утверждениях — и Бет и Чарльз уверены в том, что выпал «орел».
Но давайте рассмотрим утверждение Дейва. С одной стороны, когда Дейв говорит, что вероятность выпадения «орла» равна 60%, он врет. Но с другой стороны, если Дейв действительно уверен, что вероятность выпадения «орла» составляет 60%, то он говорит правду, исходя из степени своей уверенности.
Некоторые философы считают, что подобные случаи поддерживают плюралистический подход, при котором учитывается существование самых разнообразных вероятностей. Я же считаю, что следует рассмотреть теорию вероятностей с четвертой точки зрения — уровня поддержки.
Здесь вероятности рассматриваются как совокупность доказательств между утверждениями.
Когда Бет говорит, что «орел» выпадет с вероятностью 50%, она подразумевает, что эта вероятность зависит от ранее полученной информации — например о том, что монета симметричная. Однако, вероятность меняется относительно другой информации. Когда Чарльз говорит, что «орел» выпадет с вероятностью 75%, он имеет в виду, что вероятность равносильна информации о том, что «орел» выпал три раза из четырех. Между тем, Дэйв говорит, что вероятность выпадения «решки» составляет 60% по отношению к той же информации, но поскольку мы знаем, что «орел» выпал три раза из четырех, Дэйв лжет.
Степень уверенности объединяет все три теории и помогает решить существующие проблемы. Она помогает зафиксировать связь между вероятностью и степенью уверенности не идентифицируя их — степень уверенности должна рационально ограничиваться уровнем поддержки. Причина, по которой я должен быть на 50% уверен в том, что выпадет «орел» (при условии, что все, что мне известно о монете — то, что она симметричная), заключается в качестве доказательств, подтверждающих эту гипотезу.
Точно так же, благодаря уровню поддержки, мы знаем, что «орел» выпадал с частотой повторения 75% (что делает выпадение «орла» вероятным на 75% при любом броске). Подобный подход фиксирует связь между частотой повторенияи вероятностью, но не означает, что частота повторения и вероятность — одно и то же. Вместо этого, вероятности могут быть связаны утверждениями о частоте повторения и конкретных людях.
Наконец, тенденция к выпадению «орла» свойственна уровню поддержки, что с одной стороны, говорит о физических свойствах монеты, а с другой о вероятности выпадения «орла» или «решки» — иными словами, данный подход определяет влияют ли физические свойства монеты на ее «поведение». В более широком смысле, причину и следствие связывает предрасположенность — например, описание строения атома и гипотезу о его распаде.
Поскольку все вышеизложенное делает вероятности самостоятельными структурами, наши четыре теории подскажут как определить принцип произведения вероятностей.
Абстрактный объект — объект, созданный какой-либо абстракцией или при посредстве какой-либо абстракции; когнитивно представленный объект познания, репрезентирующий те или иные сущностные аспекты, свойства, отношения вещей и явлений окружающего мира — прим. переводчика.
Скептик может сказать, что подбрасывать монетку легко. Представьте, что вы присяжный. Как определить вероятность совершения убийства подсудимым, чтобы понять существуют ли основания для сомнения в его невиновности?
Ответ: нужно больше думать. Во-первых, задать вопрос: существуют ли доказательства совершения преступления? Мы должны выяснить, насколько убедительны эти доказательства и подтверждают ли они гипотезу о виновности подсудимого. Возможно, наше внимание привлекут отпечатки пальцев на орудии убийства.
Затем следует спросить: можем ли мы математически рассчитать вероятности, чтобы в свете доказательств опровергнуть вероятность нашей гипотезы, заменив ее более приемлемой? Теперь нас интересует вероятность причины-следствия — обвиняемый совершил убийство (причина), его отпечатки пальцев обнаружили на орудии убийства (следствие). позволяет вычислить роль трех дополнительных вероятностей: априорной вероятности причины, вероятности следствия, вызванного этой причиной, и вероятности следствия без причины.
Так как это относится к любой имеющейся у нас информации, первая вероятность (причина) определена тем, что нам известно о мотивах и возможностях подсудимого. Мы можем разобраться с третьей вероятностью (следствие без причины), разбив вероятность невиновности подсудимого на другие возможные причины смерти жертвы; узнать какова вероятность каждой из них, а так же с какой вероятностью отпечатки пальцев подсудимого могут попасть на орудие убийства. В конечном итоге, мы определим вероятность того, что другие вероятности больше не «разбиваются».
Теперь мы можем вывести общие принципы для определения вероятностей, либо опереться на интуитивные суждения, как в случае с подбрасыванием монеты.
Рассуждения о преступниках, а не о монетах, вряд ли приведут к взаимодействию вероятностей. Но альтернативы нет. Просто собирая дополнительную информацию мы не разрешим разногласия об истинности той или иной гипотезы. Добиться прогресса можно только путем философского осмысления огромного количества вероятностей, имеющейся информации и того, насколько она поддерживает одну вероятность по сравнению с другой.
Алгебра. Урок 9. Статистика, вероятности
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Оглавление страницы:
Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
Другими словами, среднее арифметическое – это дробь, в числителе которой стоит сумма чисел, а взнаменателе – их количество.
Среднее арифметрическое: ( 6 + 10 + 16 + 20 ) 4 = 52 4 = 13
Их полусумма равна: 7 + 10 2 = 17 2 = 8,5
Размах ряда чисел – это разность между наибольшим и наименьшим числом.
Для удобства упорядочим этот ряд: 1, 2, 3, 3, 8, 10, 16
Мода ряда чисел – наиболее часто встречающееся число в этом ряду.
Ряд чисел может иметь более одной моды, а может вообще не иметь моды.
Каждое число в данном ряде встречается одинаковое количество раз (один раз).
Данный ряд не имеет моды.
Вероятности
Случайное событие – это событие, которое может произойти, а может не произойти.
Мы называем событие случайным, если нельзя утверждать, что это событие в данных обстоятельствах непременно произойдёт.
События обозначаются заглавными латинскими буквами.
Частота случайного события A в серии опытов – это отношение числа тех опытов, в которых событие A произошло, к общему числу проведенных опытов.
Если решка выпала 8 раз, то орёл выпал 20 − 8 = 12 раз.
Частота: 12 20 = 6 10 = 0,6
Как мы видим, чётных чисел выпало три штуки.
Например, для события «выпало четное число очков» при броске кубика:
«выпало два очка», «выпало четыре очка», «выпало шесть очков»
«выпало одно очко», «выпало три очка», «выпало пять очков»
Сумма вероятностей всех элементарных исходов случайного эксперимента равна 1.
A = «достать кролика», посчитаем вероятность этого события. P ( A ) = m n = 0 3 = 0
A = «достать синий шар», посчитаем вероятность этого события. P ( A ) = m n = 3 3 = 1
A = «достать синий шар», посчитаем вероятность этого события. P ( A ) = m n = 3 12 = 0,25
Примеры противоположных событий:
Вероятность противоположного события определяется по формуле: P ( A ¯ ) = 1 − P ( A )
Пусть событие A : «ручка пишет плохо».
Противоположное событие: A ¯ : «ручка пишет хорошо»
P ( A ) = 0,28. Найдём вероятность противоположного события по формуле:
P ( A ¯ ) = 1 − P ( A ) = 1 − 0,28 = 0,72
Пусть событие A : «фонарик неисправен»
Противоположное событие A ¯ : «фонарик исправен»
P ( A ¯ ) = 1 − P ( A ) = 1 − 0,08 = 0,92
Теоремы о вероятностных событиях
Примеры несовместных событий:
За один бросок может выпасить либо орёл, либо решка, одновременно орёл и решка выпасть не могут.
Теорема сложения вероятностей несовместных событий:
Вероятность появления одного из двух (или более) несовместных событий равна сумме вероятностей этих событий.
P ( A + B ) = P ( A ) + P ( B )
Решение:
Событие A = «вытащить билет по теме углы» и событие B = «вытащить билет по теме треугольники» – несовместные.
Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
P ( A + B ) = P ( A ) + P ( B )
P ( A + B ) = 0,47 + 0,22 = 0,69
Решение:
Событие A = «выиграть машину», событие B = «выиграть денежный приз» и событие C = «выиграть сувенир» несовместные.
Вероятность появления одного из трех несовместных событий равна сумме вероятностей этих событий:
P ( A + B + C ) = P ( A ) + P ( B ) + P ( C )
P ( A + B + C ) = 0,001 + 0,013 + 0,04 = 0,054
Примеры независимых событий:
Примеры зависимых событий:
Теорема умножения вероятностей независимых событий:
Вероятность появления двух (или более) независимых событий равна произведению вероятностей этих событий.
P ( A ⋅ B ) = P ( A ) ⋅ P ( B )
Решение:
Событие A : «извлечь красный шар из первой шляпы».
Событие B : «извлечь красный шар из второй шляпы».
Оба этих события независимы друг от друга, так как при извлечении шпара из первой шляпы, вторая остаётся нетронутой. Найдём вероятности этих событий.
P ( A ) = 1 2 (всего шаров два, красных – один).
P ( B ) = 4 5 (всего шаров пять, красных четыре).
P ( A ⋅ B ) = P ( A ) ⋅ P ( B )
P ( A ⋅ B ) = 1 2 ⋅ 4 5 = 0,4
Решение:
Событие A : «попадание», событие B : «промах». По условию P ( A ) = 0,9. Найдём вероятность промаха, она равна
P ( B ) = 1 − P ( A ) = 1 − 0,9 = 0,1
Каждый из выстрелов – событие, не зависящее от предыдущих или последующих выстрелов, то есть все три события – независимые. Вероятность появления трех независимых событий равна произведению их вероятностей, то есть
P ( A ⋅ A ⋅ B ) = P ( A ) ⋅ P ( A ) ⋅ P ( B )
P ( A ⋅ A ⋅ B ) = 0,9 ⋅ 0,9 ⋅ 0,1 = 0,081
Симметричная монета в теории вероятности
Математическая монета, которая используется в теории вероятности, лишена многих качеств бычной моенты: цвета, размера, веса и достоинства. Она не сделана ни из какого материала и не может служить платёжным средством. Монета имеет две стороны, одна из которых орёл (О), а другая решка (Р). Монету бросают и она падает одной стороной вверх. Никаких других свойств у монеты нет. Рассмотрим различные опыты с монетой
Бросание одной монеты
Возможные исходы:
О
Р
Всего два исхода. Вероятность каждого исхода из двух возможных равна 1 2 = 0,5
Бросание двух монет (бросание одной монеты два раза подряд)
Возможные исходы:
О О
О Р
Р О
Р Р
Всего четыре исхода. Вероятность каждого исхода из четырех возможных равна 1 4 = 0,25
Бросание трех монет (бросание одной монеты три раза подряд)
Возможные исходы:
О О О
О О Р
О Р О
О Р Р
Р О О
Р О Р
Р Р О
Р Р Р
Всего восемь исходов. Вероятность каждого исхода из восьми возможных равна 1 8 = 0,125
Бросание четырех монет (бросание одной монеты четыре раза подряд)
Возможные исходы:
О О О О
О О О Р
О О Р О
О О Р Р
О Р О О
О Р О Р
О Р Р О
О Р Р Р
Р О О О
Р О О Р
Р О Р О
Р О Р Р
Р Р О О
Р Р О Р
Р Р Р О
Р Р Р Р
Всего шестнадцать исходов. Вероятность каждого исхода из шестнадцати возможных равна 1 16 = 0,0625
Решение:
Всего восемь различных исходов (см. опыт с бросанием трех монет). Исходов, в которых решка выпала ровно один раз, три.
Решение:
В опыте с бросанием четырех монет всего шестнадцать различных исходов. Благоприятные исходы – те, в которых выпало два, три или четыре орла. Таких исходов всего одиннадцать.
Симметричная игральная кость в теории вероятности
Математическая игральная кость, которая используется в теории вероятности, это правильная кость, у которой шансы на выпадение каждой грани равны. Подобно математической монете, математическая кость не имеет ни цвета, ни размера. Ни веса, ни иых материальных качеств. Рассмотрим различные опыты с игральной костью.
Бросание одной кости
Бросание двух костей (бросание одной кости два раза подряд)
Для того, чтобы перебрать все возможные варианты, составим таблицу:
Первое число в паре – количество очков, выпавших на первом кубике. Второе число в паре – количество очков, выпавших на втором кубике. Всего возможно тридцать шесть различных исходов.
Такую таблицу не составит труда нарисовать на экзамене, если попадётся задача на бросание двух кубиков. Сумма чисел в ячейке – сумма выпавших очков.
Решение:
Решение:
Презентация по математике «Теория вероятности. Симметричная монета»
Описание разработки
В данной работе рассматривается решение задачи В6 по теме «Симметричная монета». Учащимся предлагается 2 способа решения:
1) Метод перебора комбинаций;
2) Специальная формула вероятности.
Монета (лат. moneta) — денежный знак, изготовленный из металла либо другого материала определённой формы, веса и достоинства. Кроме полноценных монет выпускаются разменные, коллекционные, памятные и инвестиционные монеты. Чаще всего монеты изготавливаются из металла методом чеканки и имеют форму правильного круга.
Почти каждая монета имеет лицевую сторону — аверс, и оборотную сторону — реверс.
Аве́рс (фр. avers, лат. adversus — «обращённый лицом») — лицевая, главная сторона монеты.
Общепринятым в современных монетных каталогах считается определение аверса по следующим признакам по убыванию важности:
Портрет главы государства, монарха, монетного сеньора или другого обладателя монетной регалии.
Государственный герб, эмблема и т. п. При этом, если на обеих сторонах монеты изображены гербы, то за аверс принимается та, на которой изображён герб, более высокий по рангу и положению. Например, на монетах португальских колоний на аверсе обычно изображался герб Португалии, а на реверсе — герб колонии.
Легенда с названием страны, территории.
Легенда с именем обладателя монетной регалии, либо обозначение банка-эмитента.
Задачи на подбрасывание монет считаются довольно сложными. Тем не менее, существует как минимум два принципиально различных метода решения:
Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.
При решении задачи B6 для подготовки к ЕГЭ по математике надо знать оба метода.
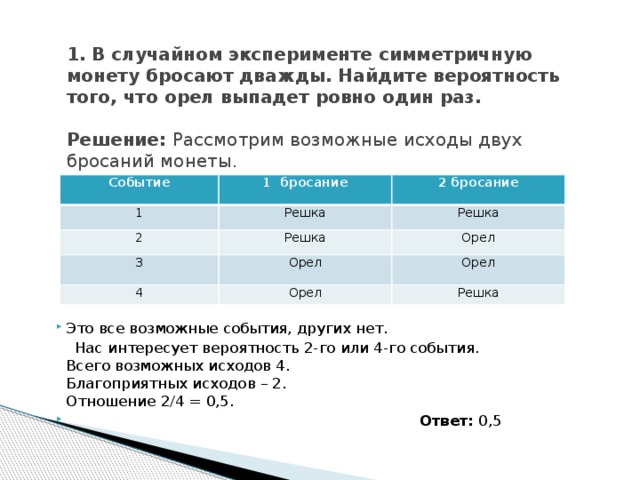
1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение: Рассмотрим возможные исходы двух бросаний монеты.
Это все возможные события, других нет.
Нас интересует вероятность 2-го или 4-го события.
Всего возможных исходов 4.
Благоприятных иcходов – 2.
Содержимое разработки
Шмидт Наталья Александровна
Монета (лат. moneta ) — денежный знак, изготовленный из металла либо другого материала определённой формы, веса и достоинства. Кроме полноценных монет выпускаются разменные, коллекционные, памятные и инвестиционные монеты. Чаще всего монеты изготавливаются из металла методом чеканки и имеют форму правильного круга.
Почти каждая монета имеет лицевую сторону — аверс, и оборотную сторону — реверс.
Общепринятым в современных монетных каталогах считается определение аверса по следующим признакам по убыванию важности:
Орёл (не тождествен аверсу ) — в дореволюционной России так именовалась в обиходе сторона монеты с изображением государственного герба. Первые общегосударственные монеты мелких номиналов, появившиеся после денежной реформы Петра I, несли на аверсе изображение двуглавого орла.
Ре́верс (лат. revertor — «поворачиваю назад») — оборотная сторона монеты, противоположная аверсу.
Реверсом принято считать сторону с номиналом монеты, хотя бывает, когда сторона с номиналом является аверсом. Реверс не тождественен решке.
Монета с точки зрения теории вероятностей лишена многих качеств настоящей монеты. У неё нет цвета, размера, веса и достоинства. Она не сделана ни из какого материала и не может служить платежным средством. Математическая монета имеет только две стороны, одна из которых называется «орел», а другая — «решка». Монету бросают, и она падает одной из сторон вверх.
Задачи на подбрасывание монет считаются довольно сложными. Тем не менее, существует как минимум два принципиально различных метода решения:
При решении задачи B6 для подготовки к ЕГЭ по математике надо знать оба метода.
Метод перебора комбинаций
Состоит из трех шагов:
1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение: Рассмотрим возможные исходы двух бросаний монеты.