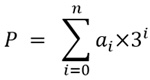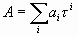Что такое симметричная система счисления

Замена двоичной логики — увеличит ли это производительность?

Наверняка на хабре уже немало постов на эту тему. Тем не менее, я попытаюсь рассказать свою точку зрения на всё это…

Однажды я прочитал в интернете про троичную систему счисления и заинтересовался. Меня мучил вопрос, а нельзя использовать в основе компьютера симметричную троичную систему счисления (СС), и даже вдруг это увеличит производительность компьютера? Мне казалось, что это возможно, и я жаждал это проверить.

Информация:
Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3. Существует в двух вариантах: несимметричная и симметричная.
В несимметричной троичной системе счисления чаще применяются цифры <0,1,2>, а в симметричной троичной системе счисления знаки <−,0,+>, <−1,0,+1>.
У некоторых людей эта логика вызывает затруднения. Они говорят, например, приведите пример подобной логики в жизни.
Человек, немного подумавший над этой логикой поймет, что она более жизненна чем двоичная. Обычный пример троичной логики в жизни связан с постоянным током: ток движется в одну сторону, в другую сторону, его нет.

Оказалось, что симметричная троичная система счисления использовалась давным-давно для решения «задачи о гирях», использовалась в компьютере Сетунь, построенном в 50-е годы в МГУ. С 2008 года в университете « California Polytechnic State University of San Luis Obispo» функционирует цифровая компьютерная система TCA2, основанная на троичной системе счисления.

В чем же плюсы троичной СС над двоичной? Рассмотрим эти плюсы:

Меньше разрядов

Емкость

Экономичность системы счисления

Экономичность системы счисления — запас чисел, который можно записать в данной системе с помощью определенного количества знаков. Чем больше запас тем экономичнее система. По затратам числа знаков (в трёхразрядном десятичном числе 3*10=30 знаков) наиболее экономична из позиционных показательных несимметричных систем счисления. Обозначим p основание системы счисления, n количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел которое при этом можно записать будет равно pn/p.

Мы рассмотрели троичную арифметику, теперь затронем логику:

В чем же проблемы двоичной логики?
1.Мощности компьютера, основанного на двоичной логике, не всегда хватает. Приведем пример. Одна из наиболее сложных систем защиты – криптосистема RSA. Вскрытие шифра RSA с длиной ключа 1024 бита (такая длина часто используется в информационных системах) займет в лучшем случае — при проведении распределенных вычислений на тысячах мощных ПК — не менее пятнадцати лет, а к тому времени данная система шифровки перестанет быть востребованной.
Докажем математически какая система счисления будет наилучшей для максимальной мощности и емкости памяти. Для этого рассмотрим функцию f(p)=p^(n/p), в которой p – основание системы счисления, а n – количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел, которое при этом можно записать, будет равно pn/p

f(p)=p^(n/p)
Для того, чтобы определить максимальное значение функции, найдем ее производную:
ln f = ln p^(n/p)
ln f =n/p* ln p
. (Я не буду приводить здесь всю математику)
n*p^(n/p-2) никогда не будет равно 0 => (1 — ln⁡ p)=0, ln p = 1, p = e
e = 2,71, а ближайшее целое число к нему – это три.
Значит, в этом плане лучшая система с целочисленным основанием — троичная.

Самое вкусненькое — рассмотрим троичные логические операции:

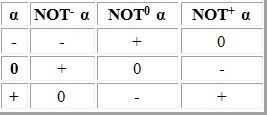
1.Отрицание

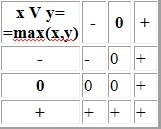
2.Конъюнкция — логическое И

3.Дизъюнкция — логическое ИЛИ

4.Операция Выбора. Эта операция существует только для троичной логики. Таблица истинности каждой из этих трёх операций содержит везде „-“, кроме единственного значения, которое ею можно выбрать.

5.Модификация. Полное название этих одноместных операций: увеличение на единицу по модулю три (INC) и уменьшение на единицу по модулю три (DEC). Увеличение на единицу по модулю три – это циклическое прибавление единицы.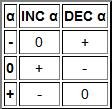

Здесь видны и прежде знакомые вам логические операции из двоичной логики, но добавились и новые…

Квантовые компьютеры

Квантовый компьютер — вычислительное устройство, работающее на основе квантовой механики. Квантовый компьютер принципиально отличается от классических компьютеров, работающих на основе классической механики.
Благодаря огромной скорости разложения на простые множители, квантовый компьютер позволит расшифровывать сообщения, зашифрованные при помощи популярного асимметричного криптографического алгоритма RSA. До сих пор этот алгоритм считается сравнительно надёжным, так как эффективный способ разложения чисел на простые множители для классического компьютера в настоящее время неизвестен. Для того, например, чтобы получить доступ к кредитной карте, нужно разложить на два простых множителя число длиной в сотни цифр. Даже для самых быстрых современных компьютеров выполнение этой задачи заняло бы больше времени, чем возраст Вселенной, в сотни раз. Благодаря алгоритму Шора эта задача становится вполне осуществимой, если квантовый компьютер будет построен.
Канадская компания D-Wave заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит. Это устройство работает на кубитах — квантовых аналогах битов.
Но можно построить компьютеры не на битах, а на кутритах — аналогах трита в квантовом компьютере.
Кутрит (квантовый трит) — квантовая ячейка, имеющая три возможных состояния.
Подлинное новаторство метода Ланьона в том, что, используя в универсальных квантовых вентилях кутриты вместо кубитов, исследователи могут существенно снизить количество необходимых вентилей.
Ланьон утверждает, что компьютер, который в обычном случае использовал бы 50 традиционных квантовых вентилей, сможет обойтись всего девятью, если будет основан на троичном представлении.
Также, согласно некоторым исследованиям, использование кутритов вместо кубитов позволит упростить реализацию квантовых алгоритмов и компьютеров.

Итог:
В конечном итоге видно, что троичная симметричная система лучше двоичной системы в некоторых показателях, но не сильно выигрывает. Но с пришествием квантовых компьютеров троичные вычисления получили новую жизнь. Универсальные квантовые логические вентили — краеугольный камень новорожденных квантовых вычислительных систем — требует сотни вентилей для завершения одной полезной операции. Квантовый компьютер канадской компании D-Wave, анонсированный в прошлом году, состоит всего из 16 квантовых битов — кубитов — минимум, необходимый для управляемого вентиля «NOT». Использование в квантовом компьютере кутритов нужно было бы намного меньше вентилей для завершения одной операции. Я думаю, если бы началось производство и тестирование таких компьютеров, то результаты были бы лучше, чем у обычных компьютеров, вскоре началось бы массовое их производство, и про двоичные компьютеры все бы забыли…

Источник

Уравновешенная (симметричная) троичная система счисления и её использование в вычислительных устройствах в докомпьютерную и компьютерную эпоху

Уравновешенная троичная система счисления обладает теми же свойствами, что и другие системы счисления (СС). СС позволяет записать число специальными знаками (цифрами). Число показывает количество подсчитанных единиц и состоит из разрядов. Разряд числа – такое условное разделение числа на единицы, когда определённое количество единиц разряда образует единицу старшего разряда, а единица разряда состоит из определённого количества единиц младшего разряда. Разряд числа имеет свой вес, вес разряда показатель того, во сколько раз единицы разряда больше или меньше единиц того разряда, с которого начинается счёт. Основание СС – это показатель того, во сколько раз единица разряда больше единицы предыдущего разряда. [1]

Уравновешенная троичная система счисления родилась из задачи “о взвешивании”. Эта задача была известна ещё Фибоначчи (ок. 1170—ок. 1250). В задаче требовалось найти наименьшее количество гирь для взвешивания на двухчашечных весах груза массой от 1 до 40 единиц, при этом гири можно было располагать на любой из чаш весов. Оказалось, что для решения такой задачи потребуются только четыре гири с весом 1, 3, 9, 27 единиц. Нетрудно заметить, что вес последующих гирь растёт точно так же, как растёт математический вес разрядов в троичной системе счисления, т. е. вес каждой последующей гири, как и вес каждого последующего разряда троичного числа, в три раза больше предыдущего веса. Т. к. гири располагаются на разных чашах весов, то их вес относительно взвешиваемого груза может иметь как положительное, так и отрицательное значение. Если мы хотим воспользоваться недостающей гирей весом в 2 единицы, то мы должны на чашу весов с грузом положить гирю с весом 1, а на противоположную с весом 3. Ясно, что это будет соответствовать весу гири в 2 единицы, т. к. вес гири 1 вычитается из веса гири 3 (см. рис.1). Таким образом, используя четыре гири, кладя их на различные чаши весов, можно получить любой вес от 1 до 40 единиц.

Целое число в уравновешенной троичной системы счисления (УТСС) можно записать по формуле

P – значение, записанное в троичное число,

i – индекс текущего разряда числа,

n – индекс последнего разряда числа,

3 i – вес разряда числа.

Отличительной особенностью УТСС от других СС является то, что отдельного знака для всего числа не существует, но при этом каждый разряд числа имеет свой знак. Является ли число, записанное в УТСС, положительным или отрицательным, определяется по знаку в старшем разряде числа. Поменять знак числа на обратный значит поменять его во всех разрядах числа. [2]

Первым человеком, реализовавшим автоматический счёт в УТСС, был англичанин Томас Фаулер. К сожалению, его счётная машина не получила государственной финансовой поддержки, и, хотя была изготовлена и продемонстрирована в мае 1840 г. Чарлзу Бэббиджу, её чертежи не были опубликованы, и она была забыта. Финансирование ушло на построение машины Чарлза Бэббиджа, которая использовала десятичное основание для вычислений, что значительно усложняло и удорожало машину. [2, 3]

В августе 2000 г. в США, Марком Глускером была создана работающая механическая счётная машина для УТСС. Машина чисто демонстрационная, имеет три троичных разряда и воспроизводит то, как могла бы осуществляться операция умножение на машине Фаулера. Тем не менее, эту машину нельзя считать моделью машины Фаулера, т. к. сохранившиеся сведения о машине Фаулера весьма скудные, это скорее предположение о том, как могла бы быть устроена машина Фаулера. [2]

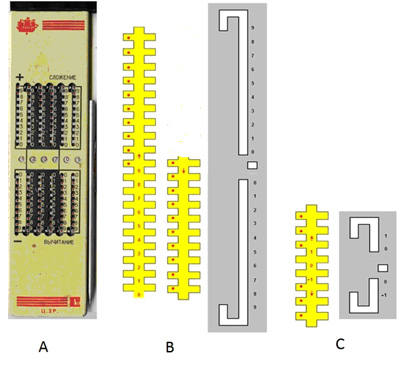
Рис. 2. Модель счётной машины Фаулера

Не вдаваясь в подробности воссозданной модели, позволим себе некоторое фантазирование и продемонстрируем насколько упрощается конструкция Счислителя Куллера (СК), если в нём использовать не десятичную СС, а УТСС. СК был подробно описан нами в [1].

Мы видим, насколько сократилась длина счётной рейки в СК. Помимо этого, появилась возможность оперировать на СК не только положительными, но и отрицательными числами, причём при получении такого существенного преимущества принцип устройства СК не изменился.

Жаль, что УТСС была использована только в одном механическом счётном устройстве (МСУ) – в счётной машине Фаулера. МСУ было бы удешевлено при использовании УТСС по сравнению с устройством, использующим десятичную СС. Однако не всё так просто, как кажется на первый взгляд. При вычисление на МСУ для УТСС необходимо производить преобразования из десятичной СС в УТСС и обратно. В счётной машине Фаулера не было шифратора и дешифратора для рассмотренных выше преобразований, преобразования осуществлялись не автоматически, а посредством специально составленных для этого таблицы, что вызывало определённые неудобства. [2]

Электронный автоматический счёт на основе УТСС был реализован на советских ЭВМ “Сетунь” (в декабре 1958 г. построен опытный образец) и “Сетунь-70” (опытный образец был готов в апреле 1970 г.) Главным конструктором ЭВМ “Сетунь” являлся заслуженный научный сотрудник МГУ Николай Петрович Брусенцов. [3, 4].

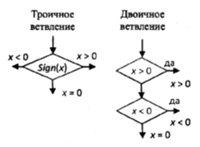
Рис.4. Троичное и двоичное ветвление

В настоящее время в ЭВМ широко используется ДСС, но правильно ли было использовать двоичное основание в электронных вычислительных устройствах? Ясно, что использование ДСС в вычислительных устройствах было прогрессом по сравнению с использованием десятичной СС, но досадно то, что на УТСС, имеющую явные преимущества перед ДСС, так мало обращали внимания изобретатели вычислительных устройств.

Источник

TREX: 27-ричная симметричная система счисления

Каждый специалист по компьютерам знает, насколько сложно работать с длинными последовательностями нулей и единиц. На помощь ему приходят восьмеричная и шестнадцатиричная системы счисления, обеспечивающие более компактное представление информации.

С троичной системой счисления ситуация хуже: есть несколько способов представления троичных чисел и есть несколько способов компактной записи троичных чисел, но они имеют недостатки, усложняющие работу с ними.

Система кодирования TREX разработана для компактного отображения симметричной троичной системы счисления при ее использовании в компьютерных системах

Замечания

В данной статье речь идет только о симметричной троичной системе счисления, использующей значения <-1, 0, +1>.

Недостатки предлагаемых на сегодняшний момент 9-ти и 27-ричных систем кодирования троичных чисел будут упомянуты ниже в сравнении с системой TREX.

Проблематика

При разработке ПО для работы с троичными компьютерами встает вопрос вывода информации на различные устройства отображения информации. При этом информация должна выводиться упорядоченно, чтобы при печати, например, дампов одинаковые разряды чисел располагались на одинаковых позиция строки.

Работа с троичной логикой очень непривычна даже для опытных программистов, поэтому для повышения удобства работы, минимизации человеческих ошибок и сокращения времени освоения троичного компьютера (который когда-нибудь уже будет создан) требуется система кодирования, обладающая простотой, наглядностью и односимвольностью ( отображением одного разряда одним символом, желательно из стандартного набора ASCII)

Представление троичных чисел

Для записи симметричной троичной системы счисления удобной формы отображения на экране компьютера можно добиться, используя алфавит <-, 0, +>.

Компактное представление троичных чисел

Поскольку с длинными последовательностями знаков «-», «0» и «+» работать неудобно (как и с длинными последовательностями «0» и «1» в двоичной системе счисления), то должна быть возможность компактного отображения информации (по аналогии с HEX-кодом).

По аналогии с названием HEX, для представляемой системы счисления предлагается использовать название TREX.

Описание системы кодирования

Система TREX использует следующий алфавит:

Троичные единицы данных и их запись в TREX

Трит

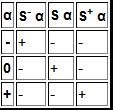
Единичный троичный разряд, который в симметричной троичной системе счисления может принимать значения <-1, 0, +1>. Для удобного отображения на устройствах вывода информации целесообразно использовать символы <-, 0, +>соответственно.

Трибл

Трибл (3 троичных разряда или 1/3 часть трайта) кодируется одним символом TREX

Трайт

Преимущества перед имеющимися 9-ти и 27-ричными системами кодирования

Предлагаемая система кодирования выгодно отличается от предлагавшихся до этого 9-ти и 27-ричных систем следующими особенностями:

односимвольностью — каждое значение отображается одним символом, не требуется вводить двухсимвольные обозначения.

Существующие системы кодирования:
существует 9-ричная система, использующая алфавит <-4,-3,-2,-1,0,1,2,3,4>

естественностью – для записи не применяются специальные символы.

Существующие системы кодирования:
существует вариант 9-тиричной системы счисления, использующий специальные символы с верхней чертой (не знаю, как нарисовать символы с верхним подчеркиванием, поэтому вставил картинку):

Свойства односимвольности и естественности очень удобны при компактном отображении на экране троичных дампов без использования специальных шрифтов.

визуальной симметричностью — для противоположных значений используются одни и те же символы с разным регистром, в отличие от систем, где противоположные значения обозначаются разными символами.

Существующие системы кодирования:
существуют 9-ричная система, использующая алфавит , и 27-ричная система, использующая алфавит <0,A..Z>).

Свойство визуальной симметричности позволяет выполнять очевидные операции с троичными числами «в уме»

Пример:
-(AdFGhb) = aDfgHB

вычисление модуля числа – модуль числа равен самому числу, если старшая цифра положительная или инвертированному числу, если она отрицательная

Пример:
mod (Mf0) = Mf0
mod (a0H) = A0h

Пример:
Mfa 00a
+ => + => 00G
mFH 00H

Пример:
Mfa > Mma
afa > bfa

Выводы

Предлагаемая система кодирования позволит:

упорядочить отображение троичной информации на экране компьютера (выровненные дампы)

уменьшить число выводимых знаков по сравнению с поразрядным выводом троичных данных

облегчить работу с троичными числами широкому кругу специалистов

уменьшить количество ошибок при разработке программного обеспечения для троичных компьютеров или их эмуляторов.

Источник

Что такое симметричная система счисления

В статье в популярной форме рассказывается о проектах «нетрадиционных» компьютеров, основанных на использовании систем счисления, отличных от двоичной: троичном компьютере «Сетунь», основанном на троичной симметричной системе счисления, «компьютере Фибоначчи», основанном на арифметике Фибоначчи, а также новых системах счисления, возникших в современной компьютерной науке, в частности, системе счисления Бергмана и кодах золотой пропорции. Основное внимание уделено троичной зеркально-симметричной системе счисления, которая может стать основой создания новых самоконтролирующихся компьютеров, основанных на «троичном принципе Брусенцова».

1. О проектах «нетрадиционных» компьютеров

Троичный компьютер «Сетунь»

Хотя современная компьютерная наука и технология, казалось бы, давно уже четко определились в своих теоретических основаниях («Неймановские Принципы»: двоичная система счисления, булева логика, двоичный элемент памяти) и на этой основе сделала потрясающие успехи в своем развитии, тем не менее, поиски новых принципов построения компьютеров продолжаются. Авторы таких «нетрадиционных» подходов с упорством, достойным, казалось бы, другого применения, доказывают преимущества предложенных ими проектов и, как потом оказывается, во многих из этих проектах, действительно, существует рациональное зерно. Любопытно, что наибольшее количество «нетрадиционных» компьютерных проектов возникло в советской науке.

Еще на заре компьютерной эры талантливый советский инженер Николай Петрович Брусенцов создал компьютер «Сетунь», основанный на троичной системе счисления, хотя вся компьютерная наука и технология того периода уже сориентировались на «двоичное» представление информации.

Идея использования троичной системы счисления при создании компьютеров пришла к Николаю Брусенцову в период его работы в Московском университете, куда он был направлен в 1953 г. на работу после окончания радиотехнического факультета Московского энергетического инчтитута. Эта система счисления позволяла создать очень простые и надежные элементы, уменьшала их количество в машине в семь раз по сравнению с другими элементами. Существенно сокращались требования к мощности источника питания, к отбраковке сердечников и диодов, и, главное, появлялась возможность использовать натуральное кодирование чисел вместо применения прямого, обратного и дополнительного кодов чисел.

Первый экземпляр «Сетуни» (а машина была названа так по имени речки, протекавшей возле университета) был готов к концу 1958 г.

Постановлением Совмина СССР серийное производство «Сетуни» было поручено Казанскому заводу математических машин. Желания наладить крупносерийное производство у руководства завода не было. Причины: «Сетунь» была слишком дешевой машиной, а значит, невыгодной для завода, и тот факт, что она надежно и продуктивно работала во всех климатических зонах от Калининграда до Магадана и от Одессы до Якутска, причем без какого-либо обслуживания и по существу без запасных частей, в расчет не принимался. Успешность испытаний вынудили 30 ноября 1961 г. директора завода был подписать акт, положивший конец его стараниям похоронить неугодную машину.

Выпускали всего по 15—20 машин в год, а вскоре и от этого отказались. Всего казанский завод выпустил 50 ЭВМ «Сетунь», 30 из них работали в высших учебных заведениях СССР.

Брусенцов Николай Петрович

И даже после того, как согласно распоряжению администрации Московского университета первый образец этого уникального компьютера, представляющего сейчас огромный исторический интерес, был разрезан на части и в буквальном смысле выброшен на мусорную свалку, автор проекта продолжал и до сих пор продолжает настаивать на преимуществах «троичного принципа». И, как это не кажется парадоксальным, постепенно компьютерное сообщество все больше начинает осознавать правоту Николая Брусенцова, и многие компьютерные специалисты (в частности, известный американский ученый, почетный профессор Станфордского университета Дональд Кнут) склоняются к тому, что компьютеры будущего вполне могут быть «троичными» компьютерами.

Очень приятно, что многие работы Н.П. Брусенцова выставлены на сайте «Академии Тринитаризма» http://www.trinitas.ru/rus/doc/avtr/00/0150-00.htm и на этом же сайте можна познакомиться с биографией Брусенцова и драматической историей создания компьютера «Сетунь».

Еще одной «нетрадиционной» компьютерной идеей, возникшей в советской науке, является проект так называемого «Компьютера Фибоначчи». Этот проект начал интенсивно развиваться в СССР после успешного выступления автора на объединенном заседании Компьютерного и Кибернетического обществ Австрии (Вена, март 1976 г.). Именно это выступление стало причиной широкого зарубежного патентования изобретений по «Компьютерам Фибоначчи» за рубежом. 65 зарубежных патентов, выданных государственными патентными ведомствами США, Японии, Англии, Франции, ФРГ, Канады и других стран, являются официальными юридическими документами, которые подтверждают приоритет советской компьютерной науки (и приоритет автора) в этом важном направлении.

Необходимо отметить, что направление развивалось весьма успешно сначала в Таганрогском радиотехническом институте (1971-1977 гг.), а затем в Винницком политехническом институте (1977-1995 гг.). Министерство общего машиностроения СССР выделило довольно значительное по тем временам финансирование (15 млн. рублей) на создание «компьютера Фибоначчи» и в Винницком политехническом институте был создан квалифицированный коллектив ученых и конструкторов для инженерной реализации «фибоначчиевых» проектов. Разработанный в середине 80-х годов 20-го века под руководством автора 18-разрядный саморректирующий аналого-цифровой преобразователь для сигналов звукового диапазона, основанный на «коде Фибоначчи», на тот момент считался одним из лучших АЦП подобного типа не только в СССР, но и за рубежом. Заложенные в его основу принципы автоматической коррекции ошибок сохраняют актуальность и до сих пор. Была также создана элементная база для проектирования самоконтролирующегося компьютера Фибоначчи.

Пик популярности данного направления пришелся на конец 80-х годов, когда СКТБ «Модуль» Винницкого политехнического института начало мелкосерийное производство «фибоначчиевых» АЦП и ЦАП, которые по своим техническим параметрам превышали мировой уровень и были использованы многими организациями Москвы, Ленинграда, Киева при создании высокоточных метрологических систем. В 1988 г. по инициативе известного немецкого кибернетика академика Кемпе автор был приглашен в Дрезденский технический университет в качестве «визитинг-порофессора» для чтения лекций по «компьютерам Фибоначчи» в университетах Дрездена, Берлина, Карлмарксштадта. Последовавшая в связи с этим публикация статьи «Вот вам и Фибоначчи!» в газете «Правда» (ноябрь 1988 г.) привлекла внимание советской научной общественности к развиваемому научному направлению и стало главной причиной специального заседания Президиума Украинской Академии наук, которое состоялось в июне 1989 г. по инциативе академика Б.Е. Патона. Статья автора по этому научному направлению, написанная по результатам его выступления в Академии наук Украины, была опубликована в академическом журнале «Вестник Академии наук Украины» и была признана лучшей статьей журнала по итогам 1990-го года.

Вcе эти реальные успехи (особенно уникальное по своим масштабам патентование изобретений по «компьютеру Фибоначчи» за рубежом) вызвавали огромное раздражение руководства Института кибернетики Академии наук Украины, потому что достижения в области патентования компьютерных изобретений Института кибернетики явно были скромнее достижений небольшого коллектива исследователей в Винницком политехническом институте. Несмотря на то, что научные исследования автора активно поддерживались ведущими специалистами Института кибернетики, среди которых прежде всего можна назвать докторов технических наук Б.Н. Малиновского, А.И. Кондалева, З.Л. Рабиновича (все они, кстати, были аспирантами С.А. Лебедева и отличались научной принципиальностью и высокой порядочностью), руководство Института кибернетики все же решило дать бой «компьютерам Фибоначчи». Рупором «антифибоначчизма» стал кибернетический журнал «Управляющие системы и машины». Именно в этом журнале по инициативе зам. главного редактора доктора наук Александра Палагина без какого-либо серьезного рецензироваения было опубликовано 2 абсурдные статьи одного «кибернетического» доктора, направленные против «компьютеров Фибоначчи» и автора научного направления. В этих статьях на автора был вылит «ушат грязи», автор был обвинен в некометентности, а научное направление по созданию «компьютеров Фибоначчи» было названо «порочным». Этими статьями сразу же воспользовались недруги автора в Винницком политехническом институте, который к тому моменту возглавил еще один «академик», к тому же, народный депутат печально известной «Верховной Рады». В результате автор вынужден был покинуть Винницкий политехнический институт и искать работу за рубежом (Ливия, 1995-1997 гг., Мозамбик — 1998-2000). В начале 2004 г. автор переехал в Канаду.

Более подробно с историей развития этого научного направления можна познакомится в статье автора «Компьютеры Фибоначчи и новая теория кодирования: история, теория, перспективы», опубликованной в электронном журнале «Перспективные информационные технологии и интеллектуальные системы» Таганрогского радиотехнического университета http://pitis.tsure.ru/files18/p5.pdf

Следует подчеркнуть, что теоретические работы в этом направлении никода не прекращались. Одной из новых компьютерных идей автора является так называемая «золотая» троичная зеркально-симметричная арифметика, которая является развитием троичной симметричной арифметики, использованной Николаем Брусенцовым при создании компьютера «Сетунь».

В 2002 г. Международный журнал «The Computer Journal» (British Computer Society) опубликовал статью автора «Brousentsov’s Ternary Principle, Bergman’s Number System and Ternary Mirror-symmetrical Arithmetic» (кстати, в публикации статьи на эту тему в журнале «Управляющие системы и машины» автору было отказано без каких-либо объяснений). Статья вызвала большой интерес западной науки. И первым ученым, кто прислал автору восторженное письмо, касающееся новой компьютерной арифметики, был известный американский ученый Дональд Кнут, почетный профессор Стэнфордского университета и автор всемирно известной книги «Искусство программирования». Автор также благодарен Николаю Петровичу Брусенцову за высокую оценку новой троичной системы счисления. Поскольку интерес к «троичным компьютерам» в современнной науке не только не уменьшается, а возрастает (особенно в связи с изобретением троичных электронных схем), автор считает своим приятным долгом ознакомить русскоязычного читателя с новой системой счисления, которая вызвала восторг у самого Дональда Кнута. И, возможно, эта статья станет толчком для новых компьютерных проектов.

2. Крупнейшее математическое открытие в истории математики

Каждый человек на земном шаре, окончивший хотя бы четыре класса начальной или «церковно-приходской» школы, знает, по меньшей мере, две полезные вещи: он умеет писать и читать и использовать десятичную систему счисления для выполнения простейших арифметических операций. И эта система кажется нам настолько простой и элементарной, что многие из нас с большим недоверием отнесутся к утверждению, что позиционный принцип представления чисел и основанная на нем десятичная система являются крупнейшими математическими открытиями за всю историю математики. И чтобы убедить читателя в этом, обратимся к мнению «авторитетов».

Пьер Симон Лаплас (1749-1827), французский физик и математик, член Парижской академии наук, почетный иностранный член Петербургской академии наук:

«Мысль выражать все числа 9 знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этой методе, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой».

Лаплас Пьер Симон (1749-1827)

М.В. Остроградский (1801-1862), русский математик, член Петербургской академии наук и многих иностранных академий:

«Нам кажется, что после изобретения письменности самым большим открытием было использование так называемой десятичной системы счисления. Мы хотим сказать, что соглашение, с помощью которого мы можем выразить все полезные числа двенадцатью словами и их окончаниями, является одним из самых замечательных созданий человеческого гения …»

Остроградский, Михаил Васильевич (1801 — 1861),

Жюль Таннери (1848-1910), французский математик, член Парижской академии наук:

«Что касается до нынешней системы письменной нумерации, в которой употребляется девять значащих цифр и ноль, и относительное значение цифр определяется особым правилом, то эта система была введена в Индии в эпоху, которая не определена точно, но, по-видимому, после христианской эры. Изобретение этой системы есть одно из самых важных событий в истории науки, и несмотря на привычку пользоваться десятичной нумерацией, мы не можем не изумляться чудной простоте ее механизма».

3. Троичная симметричная система счисления

В чем же основные преимущества троичной симметричной системы счисления, которые и стали причиной использования этой системы в компьютере «Сетунь»? Блестящий ответ на этот вопрос дает сам Брусенцов в статье «Преимущества троичной системы счисления», выставленной на Интернете http://5kr.mosuzedu.ru/darkblue04/brus.htm

4. Системы счисления с иррациональными основаниями

Система счисления Бергмана

где степень n принимает значение из множества целых чисел <0, ±1, ±2, ±3, …>. Если теперь использовать последовательность чисел t n <n=0, ±1, ±2, ±3, …> в качестве «весов разрядов» некоторой двоичной системы счисления, использующей двоичные цифры 0 и 1, то мы получим «двоичную» систему счисления с иррациональным основанием t = 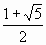, которая имеет следующее математическое выражение:

где А – произвольное действительное число, a_i – двоичные цифры, 0 или 1, i = 0, ± 1, ± 2, ± 3 …, t i – вес i-й цифры в системе счисления Бергмана, t — основание системы счисления.

На первый взгляд кажется, что «система Бергмана» не представляет собой ничего особенного по сравнению с традиционным позиционным представлением, но это далеко не так. Вся суть состоит именно в том, что основанием системы счисления является золотая пропорция t = 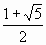, что порождает ряд весьма интересных математических свойств данной системы. Система счисления Бергмана является «избыточной», что может быть эффективно использовано для ряда практических приложений (контроль арифметических операций, коррекция ошибок в аналого-цифровых преобразователях, самосинхронизация кодовых последовательностей при передаче по каналу связи и др.).

Американский математик Джордж Бергман

Любопытно отметить, что к своему математическому открытию Джордж Бергман пришел в весьма юном возрасте, когда ему было всего лишь 12 лет! Несмотря на молодость автора, его статья была опубликована в весьма престижном американском математическом журнале «Mathematics Magazine» и по этому поводу широко известный публицистический журнал «Times» даже взял интервью у юного математического дарования Америки. В настоящее время Джордж Бергман работает профессором кафедры математики University of California (USA). Он является соавтором двух математических книг «An Invitation to General Algebra and Universal Constructions» (1998) и «Co-groups and Co-rings in Categories of Associative Rings» (1996), а также автором многих статей в области дискретной математики. Сейчас трудно сказать: имеют ли математические работы Бергмана большее значение, чем его оригинальная система счисления, которую он изобрел в юном возрасте. Несомненно одно. Имя американского математика Джорджа Бергмана широко известно в современной науке прежде всего благодаря его уникальной системе позиционного представления чисел.

Коды Золотой Пропорции

Свое дальнейшее развитие система счисления Бергмана получила в книге автора «Коды Золотой Пропорции», опубликованной издательством «Радио и связь» (Москва) в 1984 г. В книге была исследованы системы счисления следующего вида:

,

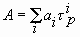
где A – некоторое действительное число, t _р — золотая р-пропорция, которая является основанием новой системы счисления, a_i – двоичная цифра i-го разряда, i = 0, ± 1, ± 2, ± 3, …, р – заданное целое число, которое может принмать значение 0, 1, 2, 3.

Более подробно с понятием «золотой р-пропорции» можно познакомиться в статье автора «Сакральная Геометрия и Математика Гармонии», выставленной на сайте «Академия Тринитаризма» http://trinitas.ru/rus/doc/0202/010a/02020028.htm

Эта формула задает новый класс позиционных представлений чисел, названных автором «Кодами Золотой Пропорции». Заметим, что приведенная выше формула задает бесконечное число новых двоичных представлений действительных чисел, так как каждому р соответствует свое двоичное представление. В частности, при р=0 «код золотой пропорции» сводится к классическому двоичному представлению, лежащему в основе современных компьютеров, а при р=1 – к системе счисления Бергмана. Заметим также, что, за исключением случая р=0 (классическая двоичная система счисления), все остальные системы счисления этого типа являются системами счисления с иррациональными основаниями. Это порождает некоторые необычные математические свойства «кодов золотой пропорции» и системы счисления Бергмана. Например, доказано, что представление натуральных чисел в любом «коде золотой пропорции» и системе Бергмана всегда является конечным, то есть любое натуральное число всегда представляется в виде конечной суммы степеней золотой р-пропорции! Например, для случая р=1 (система счисления Бергмана) имеют место следующие представления для начального отрезка натуральных чисел:

1 = 1,0; 2 = 10,01; 3 = 100,01; 4 = 101,01; 5 = 1000,1001; 6 = 1010,0001; 7 = 10000,0001

Все эти двоичные коды представляют собой ни что иное, как сокращенные изображения некоторых сумм степеней «золотой пропорции». Например, кодовое представление числа 5 = 1000,1001 в системе счисления Бергмана представляет собой ни что иное, как сокращенное изображение следующей суммы:

Книга «Коды Золотой Пропорции» стала стала своебразным научным бестселлером советской науки, тираж в 10 000 экземпляров разошелся в течении одной недели (!), а знаменитый научно-популярный журнал «Техника – Молодежи» посвятил этой книге один из своих номеров (№7, 1985 г.). в котором опубликовал статью автора «Коды Золотой Пропорции, или Системы счисления для ЭВМ будущего?», и при этом разместил весьма красочную информацию об этой книге на задней обложке номера.

Книга «Коды Золотой Пропорции» (1984) и журнал «Техника – Молодежи» (№7, 1985), посвященный этой книге

Существенно подчеркнуть, что система счисления Бергмана и «коды золотой пропорции» переворачивают наши традиционные представления о позиционных системах счисления, более того – традиционное соотношение между числами рациональными и иррациональными. В «кодах золотой пропорции» основанием, то есть началом счисления, являются некоторые иррациональные числа (типа «золотой р-пропорции» t _р). С помощью таких представлений, частным случаем которых является система счисления Бергмана, можно представлять все другие числа, включая натуральные, дробные и иррациональные числа. И поэтому с достаточной смлостью можна утверждать, что система счисления Бергмана и «коды золотой пропорции», возможно, являются наиболее революционным открытием в теории позиционных систем счисления после изобретения вавилонянами позиционного принципа представления чисел и открытия индусами десятичной системы счисления.

5. Троичная зеркально-симметричная арифметика

Зеркально-симметричное представление целых чисел

Новая троичная аитфметика, изобретенная втором, является оригинальным синтезом троичной симметричной системы счисления, которую использовал Николай Брусенцов в своем компьютере «Сетунь», и системы счисления Бергмана. Для пояснения сути нового троичного способа представления чисел и новой троичной арифметики рассмотрим бесконечную последовательность четных степеней золотой пропорции:

где t = 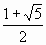— золотая пропорция.

Ясно, что указанная последовательность представляет собой геометрическую прогрессию с основанием .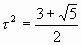

Из теории золотого сечения известно следующее интересное тождество, связывающее члены рассматриваемой последовательности:

то есть сумма двух одинаковых четных (2n-х) степеней золотой пропорции равна алгебраической сумме трех четных степеней золотой пропорции, а именно 2(n+1)-й степени, взятой со знаком «плюс», 2n-й степнени, взятой со знаком «минус», и 2(n-1)-й степени, взятой со знаком «плюс». На языке «троичных» цифр 1, 0 и ` 1 указанное тождество имеет следующую кодовую интерпретацию:

Это выражение задает правило сложения положительных единиц в новой системе счисления. Это правило гласит, что при сложении положительных единиц необходимо записать отрицательную единицу 1 в текущий разряд промежуточной суммы и сформировать симметрично относительно текущего разряда две положительные единицы, которые являются переносами в соседние (слева и справа) разряды.

Ясно, что не существует никаких проблем по аналогии записать правило сложения отрицательных единиц:

К указанным выше правилам добавим еще четыре правила, которые полностью совпадают с аналогичными правилами сложения в троичной симметричной системе счисления:

0 + 0 = 0; 1 + 0 = 1; 1 + 0 = 1 ; 1 + 1 = 0.

В результате получается следующая таблица сложения чисел в новой системе счисления. Эта таблица задает правило сложения двух одноименных троичных разрядов a_k + b_k.

Таблица зеркально-симметричного сложения

Источник