Что такое симметричное число

Мир удивительных чисел

Региональная научно практическая конференция учащихся «Первые шаги»

учащаяся 6 класса муниципального общеобразовательного учреждения «Архангельская средняя общеобразовательная школа»

село Архангельское Губкинский район Белгородская область, Россия

Позднякова И рина Владимировна,

учитель математики муниципального общеобразовательного учреждения «Архангельская средняя общеобразовательная школа»,

1.1. Историческая справка 5

1.2. Натуральные числа 6

1.3. Простые, составные 6

1.3.1. Неразгаданная тайна простых чисел 7

1.4. Числа-близнецы 9

1.5. Дружественные числа 10

1.6. Совершенные числа. 11

1.7. Хорошие числа. 11

1.8. Числа самородки. 13

1.9. Симметричные числа. 13

В учебнике 6 класса по математике в разных местах дается краткая информация о разных видах натуральных чисел. Мне захотелось изучить этот вопрос глубже и обобщить все имеющиеся сведения.

Исследован ряд натуральных чисел, обладающих любопытными особенностями, рассмотрены простые и составные числа, совершенные числа и хорошие числа. Числа-близнецы. Дружественные числа. Особенные числа. Симметричные числа

Цель работы. Изучить удивительные особенности натуральных чисел с последующим созданием презентации для использования на уроках математики

Задачи. 1. Собрать и изучить материал

2. Найти удивительное в ряде натуральных чисел.

3. Открыть какие-либо закономерности и свойства в ряду чисел

4. Обобщить полученные данные и сформулировать вывод

1. Когда я нашла в учебнике сведения о простых числах, совершенных числах, на форзаце учебника увидела таблицу простых чисел, то поняла, что авторы учебника придают натуральным числам большое значение и значит эта тема актуальна. И действительно, простые числа, составные числа, взаимно простые числа и ряд других чисел является как бы «кирпичиками» из которых «строятся» остальные натуральные числа

2. В настоящее время материал более наглядно можно представить с помощью компьютера, то решила применить ИКТ

— Применение компьютера для нахождения простых чисел, применение эффекта анимации для показа определённой группы чисел

Объект исследования: натуральные числа

Предмет исследования: нахождение простых чисел, составных чисел, совершенных чисел

— На уроках математики при изучении тем: «разложение чисел на множители», «приведение дробей к общему знаменателю»

— Созданная, красочно оформленная таблица, поможет другим учащимся разобраться в нахождении простых чисел

Освоение методов нахождения простых, составных, совершенных и других чисел, но, вероятнее всего не сможем найти самое большое простое число, совершенное число симметричное число и другие виды чисел.

1.1. Историческая справка

Числа окружают нас и всячески помогают нам в наших делах. Они – инструмент для счёта. Без чисел мы не знали бы, какой сегодня день и который час. В наши дни числа везде, и они нужны нам всегда. Трудно представить, во что превратился бы мир, если бы у нас не было чисел! Число – основное понятие математики, сложившееся в ходе длительного исторического развития. Понятие числа развивалось в тесной связи с изучением величин; эта связь сохраняется и теперь. Во всех разделах современной математики приходится рассматривать разные величины и пользоваться числами.

Потребность счёта предметов привела к возникновению понятия натурального числа. Все народы, обладавшие письменностью, владели понятием натурального числа.

Существует большое количество определений понятия «число».

Первое научное определение числа дал Эвклид в своих «Началах»: «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц».

Раньше Эвклида Аристотель дал такое определение: «Число есть множество, которое измеряется с помощью единиц».

Еще Фалес Милетский – родоначальник греческой стихийно-материалистической философии – учил, что «число есть система единиц».

Древнегреческий математик Пифагор так говорил о числе: «Число –это закон и связь мира, царящая над богами и смертными», «Сущность вещей есть число, которое вносит во всё единство и гармонию», «Всё есть число».

В своей «Общей арифметике» (1707 г) великий английский физик, механик, астроном и математик Исаак Ньютон пишет: «Под числом мы подразумеваем не столько множество единиц, сколько абстрактное отношение какой-нибудь величины к другой величине такого же рода, взятой за единицу. Число бывает трех видов: целое, дробное и иррациональное. Целое число есть то, что измеряется единицей; дробное – кратной частью единицы, иррациональное – число, не соизмеримое с единицей».

1.2. Натуральные числа

Считается, что термин «натуральное число» впервые применил римский государственный деятель, философ, автор трудов по математике и теории музыки Боэций (480 – 524 гг.), но еще греческий математик Никомах из Геразы говорил о натуральном, то есть природном ряде чисел.

Понятием «натуральное число» в современном его понимании последовательно пользовался выдающийся французский математик, философ-просветитель Даламбер ( гг.).

Первоначальные представления о числе появились в эпоху каменного века, при переходе от простого собирания пищи к ее активному производству, примерно 100 веков до н. э. Числовые термины тяжело зарождались и медленно входили в употребление. Древнему человеку было далеко до абстрактного мышления, хватило того, что он придумал числа: «один» и «два». Остальные количества для него оставались неопределенными и объединялись в понятии «много».

Росло производство пищи, добавлялись объекты, которые требовалось учитывать в повседневной жизни, в связи с чем придумывались новые числа: «три», «четыре»…

1.3. Простые и составные числа

Натуральное число называется простым, если оно имеет только два делителя: единицу и само это число.

Натуральное число называют составным, если оно имеет более двух делителей. Число 1 имеет только один делитель: само число. Поэтому его не относят ни к составным, ни к простым числам.

Первыми десятью простыми числами являются: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

Любое составное число можно разложить на два множителя, каждый из которых больше 1. Простое число так разложить на множители нельзя.

Произведение двух простых чисел может быть простым число, если одно из чисел равно 1, а другое является простым числом.

Все простые числа, большие 2, нечетные.

1.3.1. Неразгаданная тайна простых чисел

Источник

Симметричные числа. Абсолютная величина

Симметричные числа. Абсолютная величина

Симметричные числа. Абсолютная величина. Здесь для каждого действительного числа a докажем, что существует число (которое симметрично с ним) a-это условие a (a)= 0. Кроме того, достаточно ограничить себя в случае неразумного количества. Мы определяем число-a следующим образом, предполагая, что число a определяется Разделом A \ A.Низший класс A-это число-и присваивает все рациональные числа-A \ это «любое число класса A» и、 Назначьте все числа классу A для этого числа-a, где a-любое число классов A. Укажите это число-а. Теперь, убедитесь, что вы соответствуете вышеуказанным условиям. используя определение самого-b, вы можете видеть, что сумма+ (a)-это действительное число, заключенное в число в форме a-a ’и a’ a. где a и a-рациональные числа и являются as.

Построенный раздел является разделом, и легко определить действительное число (в данном случае иррациональные числа). Людмила Фирмаль

С помощью концепции симметричных чисел исчерпывается проблема чисел и действительных чисел, вычитаемых как сложение и противоположное поведение. Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Симметрия чисел

Симметрия чисел
1. Введение
В нашем мире все взаимосвязано, похоже друг на друга, имеет одинаковые или схожие параметры. Часто эти свойства называют симметрией. В «Кратком Оксфордском словаре» симметрия определяется как «Красота, обусловленная пропорциональностью частей тела или любого целого, равновесием, подобием, гармонией, согласованностью». [1 ] Очень часто симметрия проявляется в математике и физике. В физике свойства симметрии ярко проявляются в квантовой механике и ее математическом аппарате, например Уравнении Шредингера [ 2]. В математике существует специальный математический аппарат, оперирующий понятиями подобия и симметрии. Этот математический аппарат называется теорией групп [3]. Одним из практических применений симметрии в математике, является шифрование с открытым ключом “RSA” [4].

2. Матрица остатков простого числа

Рассмотрим определение вычета и сравнения по модулю. Вот определение, приведенное в современном толковом словаре. Число “ a “ называется вычетом числа “ b “ по модулю “ m “, если разность “ a – b “ делится на “ m “ ( a, b, m > 0 – целые числа ). То есть “ a “ сравнимо с “ b “ по модулю “ m “.

Это означает, что если “ a “ не делится нацело на “ m ”, то “ b “ остаток от деления “ a “ на “ m “. Два целых числа “ a “ и “ b “ сравнимы по модулю натурального числа “ m “, если при делении на “ m “ они дают одинаковые остатки.
Возьмем простое целое число и обозначим его “ b ”. Множество целых чисел в интервале (1,2,3,…b-1) обозначим “ B “. Если это множество записать в виде столбца, в порядке возрастания снизу вверх, то получим матрицу столбец. Все числа в этом столбце расположены одно за другим, их количество равно “ b – 1 “. Обозначим этот столбец номером “ 1 “. Каждое число из множества “ B “ возведем в квадрат и разделим на “ b “ с остатком. Полученные в результате деления остатки запишем в столбец. Обозначим этот столбец номером “ 2 “ и расположим его справа от столбца номер “ 1 “. Нужно расположить остатки так, чтобы они соответствовали числам, возводимым в квадрат, и находились с ними на одной прямой. После этого каждое число из множества “ B “ возведем в третью степень и разделим на “ b “ с остатком. Из полученных остатков сформируем столбец под номером “ 3 “, по аналогии со столбцом номер “ 2 “. Далее по аналогии возводим в следующую степень и находим остатки от деления на “ b “. Действия выполняем до тех пор, пока показатель степени, в которую возводим числа из множества “ B “, меньше “ b “. В результате получим квадратную матрицу размером (b-1) x (b-1).

Пример такой квадратной матрицы для простого целого числа “ b = 23 “ представлен на рис.1.

Рис. 1 Матрица остатков простого целого числа b = 23.

Полученная матрица обладает удивительными свойствами:

— Наглядно видно, что последний столбец матрицы состоит из одних единиц. Это полностью соответствует тесту простоты Ферма. A n-1 ≡ 1(mod N) [5].
— Следует отметить, что столбец с номером (b-1)/2 ( “ b “ минус 1 деленное на 2 ) состоит только из двух значений множества “ B “. Это значения 1 и ( b-1).
— Значения чисел, множества “ B “, в столбцах, симметричны относительно середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2.
— Виды симметрии для различных столбцов различны.
— Для столбцов с четными номерами, значения равноудаленные от середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2, совпадают. Для матрицы, изображенной на рис. 1, остаток от 11 в квадрате, деленное на 23 и остаток от 12 в квадрате, деленное на 23, совпадают и равны 6.
— Для столбцов с нечетными номерами, значения, равноудаленные от середины интервала, т.е. пары значений (b-1)/2 и (b+1)/2, в сумме всегда равны “ b “. Для матрицы, изображенной на рис. 1, остаток от 11 в третьей степени, деленное на 23, равен 20, остаток от 12 в третьей степени, деленное на 23, равен 3. В сумме эти два остатка равны 23, т.е. равны “ b “.

Все свойства, описанные выше и рассмотренные для матрицы, изображенной на рис. 1, присущи матрицам, построенным по таким же правилам для других простых целых чисел.

3. Матрица остатков составного числа

Матрица, рассмотренная в разделе 2, характеризует симметрию простых чисел. Для составных чисел матрица, построенная по тем же самым правилам, существенно отличается. Она наследует свойства матрицы простого числа, но приобретает и новые свойства. Рассмотрим составное число, являющееся произведением двух простых чисел “ x “ и “ y “. Точно так же величину числа обозначим “ b “, а множество всех чисел, в интервале (1,b-1), обозначим “ B “. Рассмотрим составное число “ b = 35 “, являющееся результатом перемножения простых чисел “ x = 5 “ и “ y = 7 “. Построим матрицу остатков различных степеней, для числового интервала (35-1). Матрица остатков представлена на рис. 2

Рис. 2 Матрица остатков составного числа b = 35.
Часть свойств унаследована от матрицы остатков простого числа. Так например, значения чисел, присутствующих в столбцах, симметричны относительно середины значений числового интервала, т.е. значений (b-1)/2 и (b+1)/2.

Матрица, изображенная на рис. 2, несет в себе новые свойства:

— Значения строк матрицы, у которых в первом столбце присутствуют величины кратные делителям составного числа, принимают числовые значения кратные делителям составного числа и никогда не равны 1. Например, в матрице рис. 2, строка 5, во втором столбце, имеет значение 25, в третьем 20, в четвертом 30 и так далее. Все эти значения кратны 5.
— Если исключить строки, значения которых кратны делителям числа “ b “, то обязательно найдутся два столбца, в которых остальные значения равны 1. Например, на рис. 2 это столбцы с номерами 12, 24.
— Из этих двух выбранных столбцов, наибольший номер столбца равен произведению (x-1) на (y-1). Т.е. если от каждого из сомножителей, вычесть 1 и перемножить их, то получим номер наибольшего выбранного столбца. Для матрицы на рис. 2 сомножители числа “ b “ равны 5 и 7. Если от каждого из них отнять 1 и перемножить, то получим (5-1) x (7-1) = 24. Это как раз номер наибольшего выбранного столбца. Следует отметить, что в данном случае, номер столбца равен функции Эйлера, значение которой равно (x-1) x (y-1) = ѱ(n). [6].
— Во втором столбце обязательно присутствуют четыре значения равные 1. Для матрицы остатков простого числа и значений множества “ B “равных (1,b-1), величины во втором столбце принимают значение 1. Для матрицы остатков составного числа, обязательно существуют еще два числа множества “ B “, при возведении которых в квадрат и делении на “ b “, остаток равен 1. На рис. 2 это числа 6 и 29.
— Всегда присутствуют пары чисел, множества “ B “, следующих друг за другом, значения которых, кратны делителям “ x “ и “ y “ числа “ b”. Для матрицы на рис. 2 это пары ( 14, 15 ) и ( 20, 21 ).

Все свойства, описанные выше и рассмотренные для матрицы, изображенной на рис. 2, присущи матрицам, построенным по таким же правилам для других составных целых чисел.

4. Факторизация чисел

Если рассмотреть метод шифрования с открытым ключом RSA [4], то его использование основано на существовании взаимно противоположных отображений в матрице остатков составного числа. Если взять составное число “ b “, в его матрице остатков всегда существуют два столбца “ c “ и “ d “, для которых выполняются следующие условия:

(b1**c) ≡ c1( mod b); (c1**d) ≡ d1( mod b ); b1 = d1

где b1, c1, d1 числовые значения в столбцах 1, c, d.

То есть для составного числа “ b “ всегда существует два числа “ c “, “ d “ из диапазона (1,b-1), для которых справедлива последовательность действий:
— Определим остаток любого числа “ b1 “, из диапазона (1,b-1), возведенного в степень “ c “ и деленного на “ b “. Обозначим этот остаток “ c1 “.
— Полученный остаток “ c1 “ возведем в степень “ d “ и разделим на “ b “ с остатком. Обозначим этот остаток “ d1 “.
— Полученный остаток “ d1 “ всегда равен “ b1 “.
Для алгоритма шифрования RSA, (c,b) – открытый ключ, (d,b) – секретный ключ.

Рис. 3 Матрица остатков составного числа b = 33.

Рассмотрим матрицу остатков числа b = 33, рис. 3. Для этого числа c = 3, d =7. Возьмем любое число из первого столбца, например 8 и возведем его в 3 степень, остаток равен 17. Число 17 возведем в степень 7, остаток равен 8, т.е. этот остаток равен исходному числу из первого столбца.
RSA один из распространенных алгоритмов шифрования с открытым ключом. Вместе с совершенствованием методов шифрования, совершенствуются методы дешифровки секретных сообщений.
Часто задачу дешифровки для RSA, пытаются решить в лоб, т.е. найти делители базового составного числа. Эти методы называются факторизацией чисел. Кроме простого перебора значений и проверки чисел, используют метод квадратичного решета.

Основы этого метода в том, что часть остатков от возведения в квадрат и деления на число “ b “, являются полными квадратами чисел. На рис. 2 полными квадратами являются квадратичные остатки чисел (11, 12, 17), из первого столбца. Для нахождения делителей числа “ b “, необходимо из квадратичного остатка извлечь квадратный корень. Результат, т.е. квадратный корень, вычесть из числа “ b “ или сложить с числом “ b “. Будут получены числа кратные делителям числа “ b”. Используя алгоритм Евклида можно найти делители числа “ b “.
На рис. 2, для числа 11, квадратичный остаток равен 16. Извлекаем из 16 корень квадратный, он равен 4. К 11 прибавляем 4, получаем 15, число кратное делителю 5. От 11 отнимаем 4, получаем 7, число равное делителю 7.

Одним из самых современных методов факторизации чисел, является метод решета числового поля [7]. Этот метод позволяет сократить количество проверяемых значений и уменьшить время проведения вычислений. Использование метода решета числового поля и свойств матрицы остатков составного числа, позволяет достичь еще более весомых результатов.

Для экспериментальной проверки методов факторизации чисел можно использовать, так называемые, числа Мерсенна [8]. Эти числа представляют собой число 2 в степени “ n “, минус 1, где “ n “ натуральное число. Только ограниченное количество чисел Мерсенна являются простыми, остальные разлагаются на конечное количество делителей.
Как наглядный пример, один из делителей, числа 2 в степени 4099, минус 1, равен –
431654595928296534254101974033397155588925169723783332084380283993261
209600632883153055473166663136594966053411838575253500155337120152873
781979635198920643526624304319945635699208877607737201529464080041890
547345467573782661041054825447947267620282789541695832747170633177331
920343746996221855049648583763367504662477325712779883313257418325242
923223374882540094860518718525171060169694349915604794431233943848839
032331927197514745282594881581533286782002526616104836932259305133211
436643050243706215479754994805351437606942854754835739144357537526269
041212016993538655106720507482318994547865735219931202814880677303379
021540170667630675512896640229254326407201860556265718380698467494757
374722667518146123812589844575734597771351069823560862537030159862538
798769879690913001816439118925869829536250846639469310212937581855933
518710668619729641309263324784218037304674615635505157625365285797298
443305108038716358762651248086440048468372406494047491988831492829285
161751678332086837187972136968851829414833128243888620308340321378185
123642015152620056914762030047166652837911735649104226834442937368573
819974224203735488718107356908123314371578553175076071717675764345142
549580867720367836084289513946899287311856029114297

Источник

Симметрия (в математике)

1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости a в пространстве (относительно прямой а на плоскости), ‒ преобразование пространства (плоскости), при котором каждая точка М переходит в точку M’ такую, что отрезок MM’ перпендикулярен плоскости a (прямой а ) и делится ею пополам. Плоскость a (прямая а ) называется плоскостью (осью) С.

Простейшими видами пространственной С., помимо С., порожденной отражениями, являются центральная С., осевая С. и С. переноса.

Комбинации С., порожденные отражениями и вращениями (исчерпывающие все виды С. геометрических фигур), а также переносами, представляют интерес и являются предметом исследования в различных областях естествознания. Например, винтовая С., осуществляемая поворотом на некоторый угол вокруг оси, дополненным переносом вдоль той же оси, наблюдается в расположении листьев у растений ( рис. 8 ) (подробнее см. в ст. Симметрия в биологии). С. конфигурации молекул, сказывающаяся на их физических и химических характеристиках, имеет значение при теоретическом анализе строения соединений, их свойств и поведения в различных реакциях (см. Симметрия в химии). Наконец, в физических науках вообще, помимо уже указанной геометрической С. кристаллов и решёток, приобретают важное значение представления о С. в общем смысле (см. ниже). Так, симметричность физического пространства-времени, выражающаяся в его однородности и изотропности (см. Относительности теория ), позволяет установить т. н. сохранения законы ; обобщённая С. играет существенную роль в образовании атомных спектров и в классификации элементарных частиц (см. Симметрия в физике).

Лит.: Шубников А. В., Симметрия. (Законы симметрии и их применение в науке, технике и прикладном искусстве), М. ‒ Л., 1940; Кокстер Г. С. М., Введение в геометрию, пер. с англ., М., 1966; Вейль Г., Симметрия, пер. с англ., М., 1968; Вигнер Е., Этюды о симметрии, пер. с англ., М., 1971.

Источник

Симметрия в алгебре

В работе приведен пример симметричных чисел, графиков и уравнений

Просмотр содержимого документа
«Симметрия в алгебре»

Симметрия в алгебре

Выполнила: Галиева Анастасия 9 В

Учитель: Иванченко Ирина Алексеевна

Симметрия (от греч. symmetria — соразмерность) пропорциональность, соразмерность в расположении частей целого в пространстве, полное соответствие (по расположению, величине) одной половины целого другой половине.

Рассмотрим три основных вида симметрии:

Симметрию относительно точки называют центральной симметрией.

Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Например: точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.

Зеркальная симметрия-это отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно плоскости а.

Примеры числовых симметрий

В записи чисел: 101,1221,67076 и т.д.

Симметрия в выражениях:

Другие примеры симметрических уравнений:

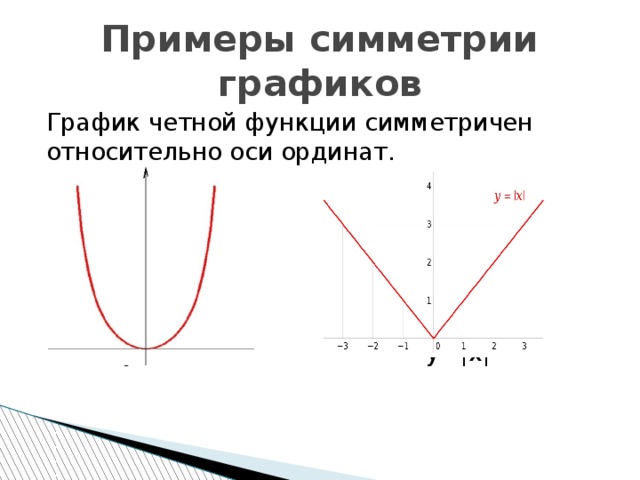
Примеры симметрии графиков

График четной функции симметричен относительно оси ординат.

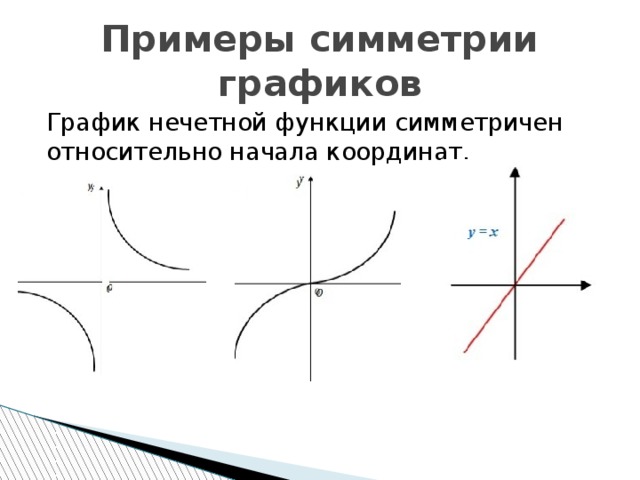
Примеры симметрии графиков

График нечетной функции симметричен относительно начала координат.

Симметрия в широком смысле-это неизменность при каких либо преобразованиях. Математики издавна стремились к красоте математических формул и справедливо считали, что красивая формула отличается от некрасивой тем, что в красоте больше симметрии. И такие «красивые» формулы не только делают преобразования красивыми, но и значительно облегчают вычислительную работу

Источник