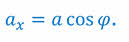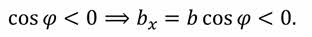Что такое система координат в физике 9 класс определение кратко

Система отсчета

Система отсчета – это совокупность тела отсчета, со связанной с ним системой координат и прибором для измерения времени.

Что такое система отсчета. Афинная и декартовая системы координат

Если рассматривать все системы отсчета относительно кинематики – они аналогичные. В кинематике не указываются преимущества одной системы отсчета при сравнении с другой. Для удобства решения выбирается наиболее приемлемая система.

Чтобы описать пространство, в котором происходит движение материальной точки, система отсчета связывается с пространственной системой координат.

Системой пространственных координат называют совокупность определений, которая может реализовать метод координат, то есть определение положения точки или тела с помощью чисел или символов.

Числа, способные указать положение выбранной точки в трехмерном пространстве, называются координатами этой точки.

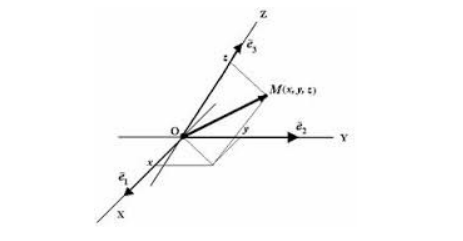
Аффинная система координат – это три линейно независимых вектора (координатных осей), выходящие из одной точки, то есть из начала отсчета.

Чтобы однозначно определить положение точки М в пространстве, то предполагают наличие зависимости радиус-вектора r → от параметра t (времени) таким образом, что каждому значению параметра t соответствует одно значение функции:

Данное равенство получило название кинематического уравнения движения материальной точки М в векторной форме.

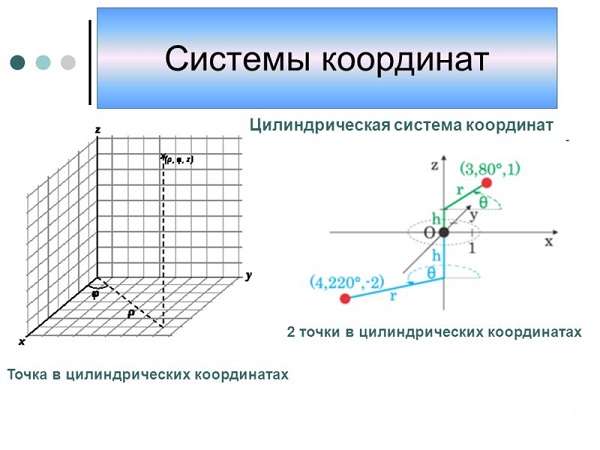
Цилиндрическая и сферическая системы координат

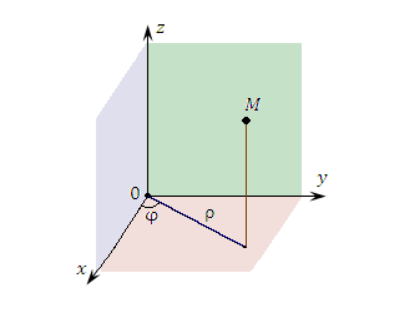
Чтобы описать криволинейное и аффинное движение, применяют криволинейные системы координат, которые упрощают форму записи законов движения тел для облегчения вычисления. Чаще всего используют цилиндрические и сферические системы координат.

Связь между декартовыми и цилиндрическими координатами может быть задана при помощи формул:

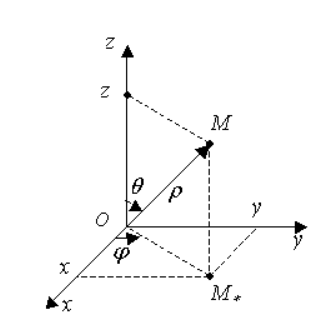
Рисунок 4 показывает, что можно вывести формулы, связывающие сферические и декартовые координаты:

Рисунок 4 . Сферические координаты точки М

Имеются другие системы криволинейных координат, с помощью которых возможно нахождение координат заданной точки: параболические, гиперболические, эллиптические и другие.

Система отсчета выбирается индивидуально относительно каждого случая в отдельности, учитывается особенность движения тела, с помощью которой определяется наиболее простой закон движения заданного тела или точки.

Источник

Механическое движение и его характеристики

теория по физике 🧲 кинематика

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

По характеру движения точек тела выделяют три вида механического движения:

По типу линии, вдоль которой движется тело, выделяют два вида движения:

По скорости выделяют два вида движения:

По ускорению выделяют три вида движения:

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

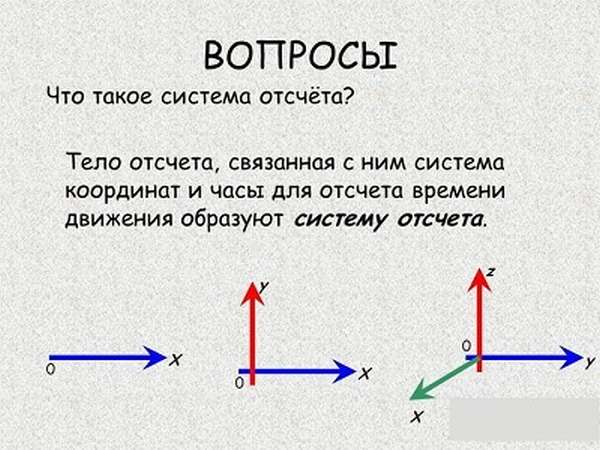
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

Способы описания механического движения

Описать механическое движение можно двумя способами:

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

Перемещение

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет вид:

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

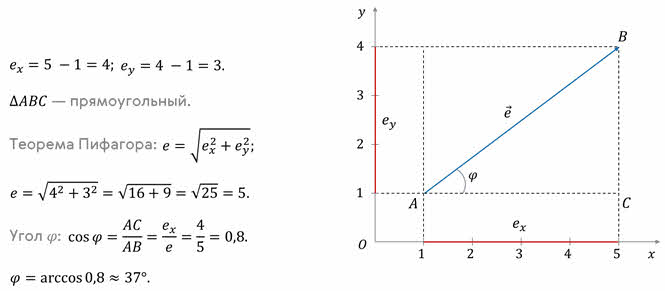
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

Точка В имеет координаты (5; 10).

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Какие бывают системы отсчета в физике и что это такое

Для решения задач механики необходимо определить положение тела в пространстве. Только тогда можно будет рассматривать его движение. Для этого необходима система отсчета в физике и механике — это система координат и способ измерения времени.

Определение

Система отсчета в физике включает в себя тело отсчета, связанные с ним оси координат и прибор для измерения времени. Тело отсчета — это точка, от которой отсчитывают положение всех остальных точек. Она может быть выбрана в любом месте пространства. Иногда в качестве начальной точки выбирают несколько тел.

Что такое система координат? Она дает возможность однозначно определить положение точки относительно начальной точки. Каждой точке пространства сопоставляются числа (одно или несколько), которые откладываются на координатных осях.

Пример — шахматная доска. Каждая клетка обозначается буквой и цифрой, по одной оси идут буквы, по другой цифры. Благодаря им мы можем однозначно описать положение фигуры.

Важно! Оси обозначаются латинскими или греческими буквами. Они имеют положительное и отрицательное направление.

Наиболее распространенные в физике виды координат — это:

Это интересно! Как правильно перевести МПА атмосферы

Существует множество других вариантов координат. Можно переходить из одних в другие, преобразуя координаты с помощью уравнений.

Понятие системы отсчета (СО) включает прибор для измерения времени, другими словами, часы. Он необходим, чтобы рассматривать движение точки — изменение ее положения со временем.

Изменения положения точки относительно выбранной СО описываются уравнениями движения. Они показывают, как изменяется положение точки с течением времени.

Виды систем отсчета

В зависимости от того, какие задачи надо решить, можно выбрать те или иные системы отсчета.

Это интересно! Квантовые постулаты Нильса Бора: кратко об основных положениях

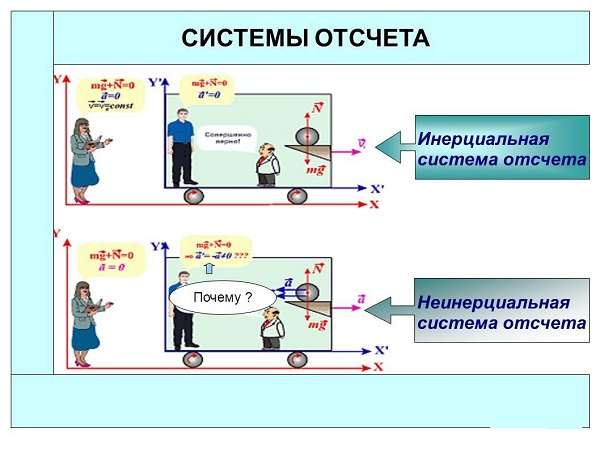
Инерциальная и неинерциальная

СО бывают инерциальные и неинерциальные. Понятие инерциальной СО важно для кинематики — раздела физики, изучающего движение тел.

Инерциальная СО движется прямолинейно с неизменной скоростью относительно окружающих тел. Окружающие предметы на нее не воздействуют. Если она стоит на месте — это тоже частный случай равномерного прямолинейного движения. Такие СО имеют следующие свойства:

Пример инерциальной СО — гелиоцентрическая, с центром в Солнце. СО, связанная с землей, инерциальной не будет. Наша планета движется вокруг солнца криволинейно, кроме того, на нее действует гравитация Солнца. Однако для многих задач этим ускорением и воздействием Солнца можно пренебречь. Это задачи, где «место действия» поверхность Земли. Например, если нам нужно найти скорость снаряда, выпущенного из пушки, влияние Солнца и вращение Земли нас не интересует.

Неинерциальная СО подвергается воздействию других предметов, поэтому движется с ускорением. К неинерциальным относятся и вращающиеся СО. В неинерциальных СО законы Ньютона не выполняются, но можно описывать перемещение теми же уравнениями, что и в ИСО, если ввести дополнительные силы.

Система центра масс и лабораторная

В механике также используется система центра масс (центра инерции), сокращенно с.ц.м. или с.ц.и. В качестве начала координат в такой СО выбирают центр масс нескольких объектов. Сумма их импульсов в такой СО равна нулю.

Применяют с.ц.и. чаще всего в задачах рассеяния. Задачи такого типа решают в механике и ядерной физике, например, это задачи о столкновении частиц в ускорителях.

В таких задачах также используют лабораторную СО. Она противоположна с.ц.и. В ЛСО положение частиц определяют относительно покоящейся мишени, на которой рассеиваются другие частицы.

Это интересно! Формула закона полного отражения и преломления света

Полезное видео: инерциальные и неинерциальные системы отсчёта

Относительность движения

По современным представлениям, абсолютной СО не существует. Это значит, что рассматривать движение тел можно только по отношению к другим телам. Не имеет смысла говорить о том, что предмет «двигается вообще». Причина этого — свойства пространства и времени:

Важно! Во времена Ньютона считалось, что можно рассматривать движение относительно абсолютного пространства, позже — относительно эфира в электродинамике Максвелла. Разработанная Эйнштейном теория относительности доказала, что абсолютного начала отсчета быть не может.

Полезное видео: определение координат тела

Вывод

Системы отсчета в физике необходимы, чтобы рассматривать движение тел. Их можно выбирать по-разному, как удобнее для конкретной задачи, так как движение относительно. Для механики важны инерциальные СО — те, которые движутся равномерно и прямолинейно относительно других тел.

Источник

Координаты

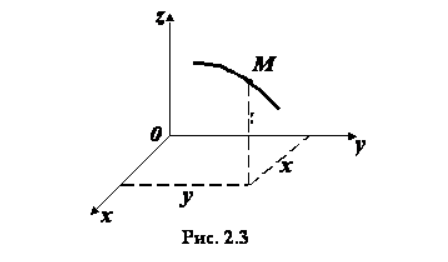
Конечно, тело может перемещаться не только вдоль прямой. Муха ползает прямо по балконным перилам, но летает по комнате замысловатым образом. Как описать такое движение? Если та же муха ползает по прямоугольному столу, ее положение можно точно определить, указав, на каких расстояниях х и у от двух соседних сторон стола она находится в любой момент времени. Числа х и у называют координатами точки (мухи) на плоскости (столе).

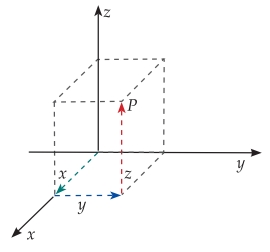
При полете мухи в комнате для определения ее положения требуются уже три числа (меняющихся со временем): расстояния до каждой из трех примыкающих друг к другу стен комнаты — х, у и z. Эти числа называются координатами точки в пространстве. Три прямые, сходящиеся в любом углу комнаты, образуют систему координат. Точка, где эти прямые сходятся, называется началом данной системы. Систему координат можно мысленно построить и без привязки к комнате. На самом деле в пространстве нет таких систем, это воображаемая конструкция, тем не менее она подходит для описания движения в самых различных ситуациях. Поскольку начало системы координат можно поместить в любую удобную для нас точку пространства, координаты тела в нем относительны, то есть зависят от выбранной системы координат.

Частицы движутся в пространстве по определенным линиям, называемым траекториями. Так, траектория Земли при движении вокруг Солнца — замкнутая кривая линия, именуемая эллипсом.

Источник

Определение координаты движущегося тела

Урок 3. Физика 9 класс (ФГОС)

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Определение координаты движущегося тела»

На прошлом уроке мы с вами говорили о пути и перемещении тела. Давайте вспомним, что путь — это скалярная величина, равная длине траектории, которую описывает тело за некоторый промежуток времени.

А перемещением называется направленный отрезок прямой, соединяющий начальное и конечное положения тела.

Так как перемещение — это векторная величина, то есть имеет модуль и направление, то складывать и вычитать перемещения необходимо по правилам сложения и вычитания векторов. Однако при решении большинства задач, используется понятие не вектора, а проекции вектора на ось координат.

— А что такое проекция вектора и каковы её свойства?

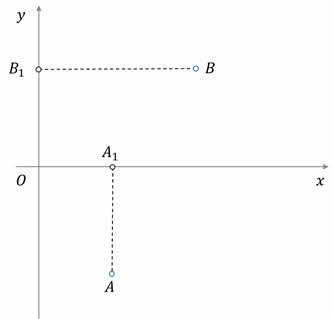
На это вопрос мы с вами и попытаемся сегодня ответить. Начнём с простого — с понятия проекция точки на ось. Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.

На представленном рисунке точка А₁ — это проекция точки А на ось Ox, а точка B₁ — проекция точки B на ось Oy.

Теперь разберёмся с проекцией вектора на ось. Согласно определению, проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «плюс» или «минус».

Знак «плюс» берут, если угол между вектором и осью острый, а «минус» — если угол тупой.

Обозначать проекцию вектора будем той же буквой, что и вектор, но с индексом внизу (например, a_x — это проекция вектора a на ось Ox).

— А если вектор перпендикулярен оси?

Тогда проекция этого вектора равна нулю.

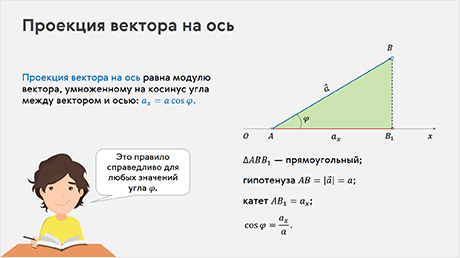
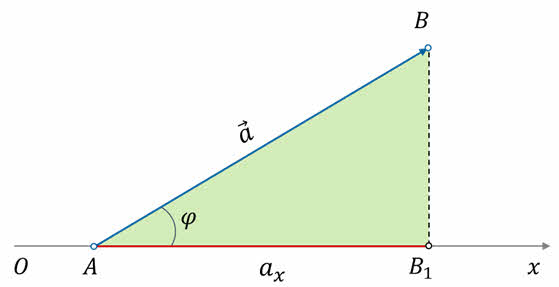
Проекцию вектора можно выразить через его модуль и угол между вектором и осью. Итак, пусть у нас есть вектор a направленный под некоторым острым углом к координатной оси Ox. Укажем проекцию этого вектора на ось.

У нас с вами получился прямоугольный треугольник, гипотенуза которого равна длине вектора a, а катет AB₁ — это проекция вектора a на ось Ox.

Тогда, на основании определения косинуса острого угла, мы можем записать, что проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью:

— А можно ли найти модуль и направление вектора по его проекциям на координатные оси?

Чтобы ответить на этот вопрос рассмотрим вектор, лежащий в плоскости xOy. Вектор, лежащий в заданной плоскости, определяется двумя проекциями на оси координат.

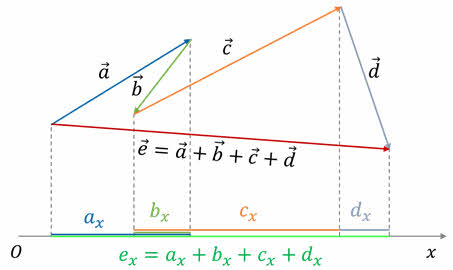
Обратим внимание на важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.

Но вернёмся к нашему прошлому уроку. На нём мы с вами говорили о том, что положение тела, которое совершило некоторое перемещение, можно найти графически. Для этого достаточно отложить вектор перемещения от начального положения этого тела. Однако в большинстве случаев необходимо уметь вычислять положение тела, то есть уметь определять его координаты. Давайте на примере решения задачи посмотрим, как можно определить координату движущегося тела, зная координату его начального положения и вектор перемещения.

Итак, два поезда идут по параллельным путям в противоположных направлениях и встречаются в шестидесяти километрах к востоку от железнодорожного вокзала. Продолжив движение через некоторое время t первый поезд удалился от места встречи на 50 километров в восточном направлении, а второй — на 80 километров в западном. Определите координаты каждого поезда относительно вокзала и расстояние между ними через промежуток времени t.

Источник