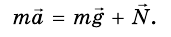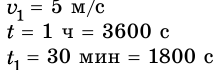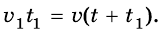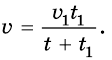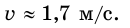Что такое система отсчета пример

Система отсчёта в физике — что это, определение и виды

Определение понятия система отсчёта в физике и механике включает в себя совокупность, которая состоит из тела отсчёта, системы координат, а также времени. Именно по отношению к этим параметрам изучается движение материальной точки или же состояние её равновесия.

С точки зрения современной физики, всякое движение можно признать относительным. Таким образом, любое движение тела можно рассматривать исключительно по отношению к другому материальному объекту или же совокупности таких объектов. Например, мы не можем указать, каков характер движения Луны в общем, но может определить её перемещение относительно Солнца, Земли, Звёзд, других планет и пр.

В ряде случаев подобная закономерность бывает связана не с единой материальной точкой, а с множеством базовых точек отсчёта. Эти базовые тела отсчёта могут задавать совокупность координат.

Основные составляющие

Основными составляющими любой системы отсчёта в механике можно считать следующие компоненты:

Для того чтобы решить конкретную задачу, необходимо определить наиболее подходящую для этого сетку координат и структуру. Идеальные часы в каждой из них потребуются лишь одни. В этом случае начало, тело отсчёта и векторы координатных осей можно выбирать произвольно.

Основные свойства

Эти структуры в физике и геометрии имеют ряд существенных различий. К физическим свойствам, которые учитываются при построении и решении задачи, относятся изотропность и однородность.

Под однородностью в физике принято понимать тождественность всех точек в пространстве. Этот фактор имеет в физике немаловажное значение. Во всех точках Земли и Солнечной системы в целом законы Ньютона в физики действуют абсолютно идентично. Благодаря этому начало отсчёта может быть размещено в любой удобной точке. И если исследователь поворачивает сетку координат вокруг начальной точки, при этом никакие другие параметры задачи не будут изменяться. Все направления, которые начинаются от этой точки, имеют абсолютно тождественные свойства. Такая закономерность называется изотропностью пространства.

Это интересно: энтропия — это что такое, где применяется термин?

Виды систем отсчёта

Существует несколько видов — подвижные и неподвижные, инерциальные и неинерциальные.

Если такая совокупность координат и времени требуется для проведения кинематических исследований, в этом случае все подобные структуры являются равноправными. Если же речь идёт о решении динамических задач, предпочтение отдаётся инерциальным разновидностям – в них движение имеет более простые характеристики.

Инерциальные системы отсчёта

Инерциальными называют такие совокупности, в которых физическое тело сохраняет состояние покоя или продолжает равномерно передвигаться, если на него не воздействуют внешние силы или суммарное воздействие этих сил равняется нулю. В этом случае на тело действует инерция, что и даёт название системе.

Одна и та же совокупность в одном случае может считаться инерциальной, а в другом будет признана неинерциальной. Это происходит в тех случаях, когда погрешность в результате неинерциальности слишком ничтожна и ею можно свободно пренебречь.

Неинерциальные системы отсчёта

Неинерциальные разновидности наравне с инерциальными связываются с планетой Земля. Учитывая космические масштабы, считать Землю инерциальной совокупностью можно весьма грубо и приблизительно.

Отличительной чертой неинерциальной системы является то, что она перемещается по отношению к инерциальной с некоторым ускорением. В этом случае законы Ньютона могут утратить свою силу и требуют введения дополнительных переменных. Без этих переменных описание такой совокупности будет недостоверным.

Проще всего рассматривать неинерциальную систему на примере. Такая характеристика движения характерна для всех тел, которые имеют сложную траекторию движения. Наиболее ярким примером такой системы можно считать вращение планет, в том числе и Земли.

Движение в неинерциальных системах отсчёта впервые изучено Коперником. Именно он доказал, что движение с участием нескольких сил может быть весьма сложным. До этого считалось, что движение Земли относится к инерциальным и описывалось оно законами Ньютона.

Источник

Содержание:

Инерциальные системы отсчета:

Вы уже знаете, что движение и покой относительны. Если относительно одной системы тело находится в состоянии покоя, то относительно других систем отсчета тело может двигаться. Рассмотрим, например, шайбу, лежащую на ледовой площадке. Шайба находится в покое относительно льда (Земли), потому что влияние на нее Земли компенсируется влиянием льда. Но для хоккеиста, движущегося мимо шайбы прямолинейно и равномерно, она движется прямолинейно и равномерно в противоположную сторону. Таким образом, одно и то же тело (шайба) относительно одной системы отсчета (связанной с Землей) находится в покое, относительно другой (связанной с хоккеистом) движется прямолинейно и равномерно. Но хоккеист ударил по шайбе клюшкой (рис. 276).

В итоге очень непродолжительного действия клюшки шайба начинает двигаться, приобретая некоторую скорость. Интересно, что после удара, когда действие клюшки на шайбу уже прекратилось, шайба продолжает движение. Тем временем после удара влияние на шайбу других тел осталось таким же, как и до удара: как и раньше, действие Земли компенсируется действием льда, а клюшка, как и до удара, никакого влияния на движение шайбы не оказывает. Шайба после удара движется по прямой линии с почти постоянной скоростью, сообщенной ей в момент удара. Но шайба в конце концов остановится, хотя из опыта известно: чем более гладкими будут лед и шайба, тем более длительным будет движение шайбы. Поэтому можно догадаться, что если совсем устранить действие льда на подвижную шайбу (это действие называют трением), то шайба продолжала бы двигаться относительно Земли с постоянной скоростью без остановки.

Этот пример и много других, подобных ему, является проявлением одного из основных законов механики, который называют первым законом движения, или первым законом Ньютона.

Инерциальные системы отсчета

Существуют такие инерциальные системы отсчета, относительно которых тело, движущееся поступательно, сохраняет свою скорость постоянной, если на него не действуют другие тела (или действие других тел уравновешено).

Само явление сохранения скорости движения тела (в частности, состояние покоя) при компенсации внешних действий на тело называют инерцией. Поэтому первый закон Ньютона часто называют законом инерции. Повседневное выражение «движение по инерции» и означает движение тела с постоянной скоростью, когда действие других тел уравновешено.

В первом законе Ньютона речь идет о равномерном прямолинейном движении. Движение мы можем рассматривать только в какой-либо системе отсчета. Возникают вопросы: в какой же системе отсчета выполняется первый закон? Можно ли считать, что он выполняется в любой системе отсчета? Закон инерции выполняется не во всех системах отсчета.

Возникает вопрос: существуют ли строго инерциальные системы? Ньютон, формулируя закон инерции и включая его в основные законы динамики, утверждал этим, что такие системы отсчета в природе существуют. В действительности, если в природе имеет место закон инерции, то должна существовать и такая система отсчета, где он выполняется абсолютно строго, то есть инерциальная система отсчета. А если существует хотя бы одна такая система, то из этого следует, что их есть бесчисленное количество, потому что всякая система отсчета, движущаяся равномерно и прямолинейно относительно инерциальной, будет также инерциальной.

Поскольку сила одна и та же, то какая-то величина должна быть одинакова для всех тел, которые ускоряются этой силой. На опыте и выясним, что это за величина.

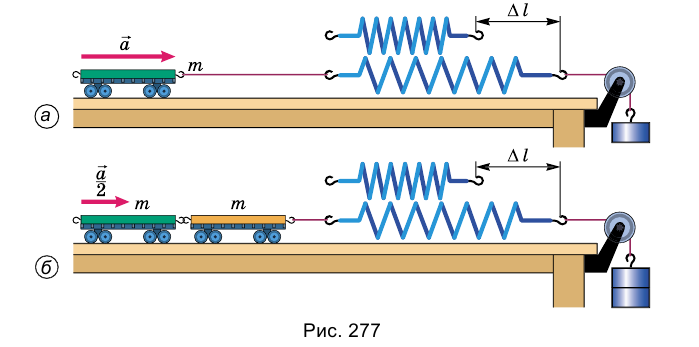
Опыт. К тележке, масса которой известна (т), прикрепим один конец пружины, а второй ее конец прикрепим к нити с грузом, переброшенной через блок (рис. 277, а). Вследствие притягивания к Земле груз движется вниз и растягивает пружину. Она, растянутая на определенную длину Д(, действует силой упругости на тележку и сообщает ему ускорение. Это ускорение можно измерить, например, оно равно а.

Это дало Ньютону основание утверждать, что сила определяется произведением массы тела и его ускорения, и сформулировать важнейший закон механики, который назвали вторым законом Ньютона.

Сила, действующая на тело, определяется произведением массы тела и его ускорения, предоставленного этой силой.

Формулу, выражающую второй закон Ньютона, следует записывать в таком виде: 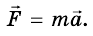Из этой формулы можно получить выражение для

ускорения движения тела 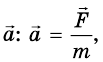из которого видно, что ускорение тела

всегда направлено так же, как и сила, вызывающая его.

Ускорение движения тела прямо пропорционально силе, приложенной к нему, и обратно пропорционально массе тела и направлено в сторону действия силы.
Следует заметить, что второй закон Ньютона, как и первый, выполняется лишь для материальных точек. В случае действия сил на протяженное тело второй закон описывает ускорение не всего тела, а только его центра масс. При поступательном движении тела все его точки имеют одинаковые ускорения. Второй закон выполняется для всех точек.

Силы, с которыми какие-либо два тела действуют друг на друга, всегда равны по модулю и противоположны по направлению.

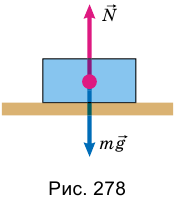
Пусть, например, на столе лежит тело (рис. 278).

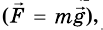
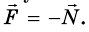
С какой силой оно действует на стол , с такой же по значению силой стол действует на тело N. Математически это записывают так: Знак «-» указывает на противоположность действия этих сил.

Третий закон Ньютона выполняется для подвижных тел

Однако равенство сил не всегда обусловлено третьим законом. Следует различать силы взаимодействия, приложенные к разным взаимодействующим телам, и так называемые равнодействующие силы, которые действуют на одно тело. Силы взаимодействия подчиняются третьему закону Ньютона, а силы, действующие на одно тело, подчиняются второму закону. Чтобы разобраться в этом подробнее, рассмотрим пример.

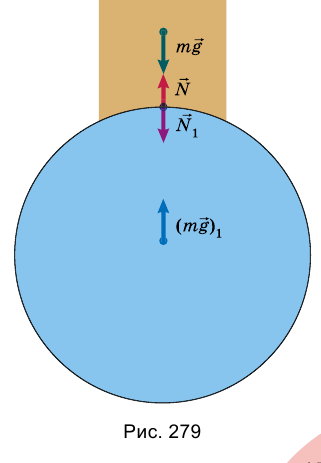
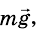
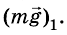
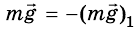
На поверхности Земли лежит тело (рис. 279). На тело действует сила , с которой его притягивает Земля. Но по третьему закону Ньютона и тело притягивает к себе Землю с такой же по значению, но противоположно направленной силой Следовательно, по третьему закону Ньютона.

Кроме гравитационного взаимодействия Земли и тела, между ними существует еще и упругое: с какой силой тело действует на Землю, с такой же силой и Земля действует на тело, то есть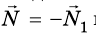по третьему закону Ньютона.

Таким образом, на тело действуют две силы: mg и N. Для этих сил, поскольку они приложены к одному телу, можно записать второй закон Ньютона:

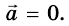
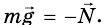
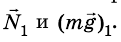
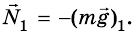
Тело находится в покое, то есть Поэтому Это равенство сил доказано на основе второго закона Ньютона. На Землю также действуют две силы: Они уравновешены, то есть Это равенство так же является следствием применения второго закона.

Пример задачи с решением

Велосипедист движется со скоростью 5 м/с. С какой скоростью двигался пешеход, вышедший из того же места на 1 час раньше, если велосипедист догнал его через 30 мин после начала своего движения?

Дано:

Решение:

Велосипедист и пешеход преодолели одинаковое расстояние, следовательно:

сюда:

Подставим значение известных величин и по-

лучим: и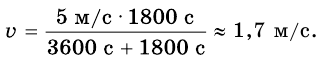
Ответ:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Система отсчёта

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями , , .

В современной физике любое движение является относительным, и движение тела следует рассматривать лишь по отношению к какому-либо другому телу (телу отсчёта) или системе тел. Нельзя указать, например, как движется Луна вообще, можно лишь определить её движение, например, по отношению к Земле, Солнцу, звёздам и т. п.

Содержание

Другие определения

Иногда — особенно в механике сплошных сред и общей теории относительности — систему отсчёта связывают не с одним телом, а с континуумом реальных или воображаемых базовых тел отсчёта, которые задают также систему координат. Мировые линии тел отсчёта «заметают» пространство-время и задают в таком случае конгруэнцию, относительно которой можно рассматривать результаты измерений.

Относительность движения

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Движущиеся тела изменяют своё положение относительно других тел. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Механическое движение — это процесс изменения относительного положения тел в пространстве с течением времени. Можно показать, что одно и то же тело может по-разному перемещаться относительно других тел.

Таким образом говорить о том, что какое-то тело движется, можно лишь тогда, когда ясно, относительно какого другого тела — тела отсчета, изменилось его положение.

Абсолютная система отсчёта

Часто в физике какую-то СО считают наиболее удобной (привилегированной) в рамках решения данной задачи — это определяется простотой расчётов либо записи уравнений динамики тел и полей в ней. Обычно такая возможность связана с симметрией задачи.

С другой стороны, ранее считалось, что существует некая «фундаментальная» система отсчёта, простота записи в которой законов природы выделяет её из всех остальных систем. Например, физики XIX в. считали что, система, относительно которой покоится эфир электродинамики Максвелла, является привилегированной, и поэтому она была названа Абсолютной Системой Отсчета (АСО). В современных представлениях никакой системы отсчёта, выделенной именно таким способом, не существует, так как законы природы, выраженные в тензорной форме, имеют один и тот же вид во всех системах отсчёта — то есть во всех точках пространства и во все моменты времени. Это условие — локальная пространственно-временная инвариантность — является одним из проверяемых оснований физики.

Источник

Какие бывают системы отсчета в физике и что это такое

Для решения задач механики необходимо определить положение тела в пространстве. Только тогда можно будет рассматривать его движение. Для этого необходима система отсчета в физике и механике — это система координат и способ измерения времени.

Определение

Система отсчета в физике включает в себя тело отсчета, связанные с ним оси координат и прибор для измерения времени. Тело отсчета — это точка, от которой отсчитывают положение всех остальных точек. Она может быть выбрана в любом месте пространства. Иногда в качестве начальной точки выбирают несколько тел.

Что такое система координат? Она дает возможность однозначно определить положение точки относительно начальной точки. Каждой точке пространства сопоставляются числа (одно или несколько), которые откладываются на координатных осях.

Пример — шахматная доска. Каждая клетка обозначается буквой и цифрой, по одной оси идут буквы, по другой цифры. Благодаря им мы можем однозначно описать положение фигуры.

Важно! Оси обозначаются латинскими или греческими буквами. Они имеют положительное и отрицательное направление.

Наиболее распространенные в физике виды координат — это:

Существует множество других вариантов координат. Можно переходить из одних в другие, преобразуя координаты с помощью уравнений.

Понятие системы отсчета (СО) включает прибор для измерения времени, другими словами, часы. Он необходим, чтобы рассматривать движение точки — изменение ее положения со временем.

Изменения положения точки относительно выбранной СО описываются уравнениями движения. Они показывают, как изменяется положение точки с течением времени.

Виды систем отсчета

В зависимости от того, какие задачи надо решить, можно выбрать те или иные системы отсчета.

Это интересно! Квантовые постулаты Нильса Бора: кратко об основных положениях

Инерциальная и неинерциальная

СО бывают инерциальные и неинерциальные. Понятие инерциальной СО важно для кинематики — раздела физики, изучающего движение тел.

Инерциальная СО движется прямолинейно с неизменной скоростью относительно окружающих тел. Окружающие предметы на нее не воздействуют. Если она стоит на месте — это тоже частный случай равномерного прямолинейного движения. Такие СО имеют следующие свойства:

Пример инерциальной СО — гелиоцентрическая, с центром в Солнце. СО, связанная с землей, инерциальной не будет. Наша планета движется вокруг солнца криволинейно, кроме того, на нее действует гравитация Солнца. Однако для многих задач этим ускорением и воздействием Солнца можно пренебречь. Это задачи, где «место действия» — поверхность Земли. Например, если нам нужно найти скорость снаряда, выпущенного из пушки, влияние Солнца и вращение Земли нас не интересует.

Неинерциальная СО подвергается воздействию других предметов, поэтому движется с ускорением. К неинерциальным относятся и вращающиеся СО. В неинерциальных СО законы Ньютона не выполняются, но можно описывать перемещение теми же уравнениями, что и в ИСО, если ввести дополнительные силы.

Система центра масс и лабораторная

В механике также используется система центра масс (центра инерции), сокращенно с.ц.м. или с.ц.и. В качестве начала координат в такой СО выбирают центр масс нескольких объектов. Сумма их импульсов в такой СО равна нулю.

Применяют с.ц.и. чаще всего в задачах рассеяния. Задачи такого типа решают в механике и ядерной физике, например, это задачи о столкновении частиц в ускорителях.

В таких задачах также используют лабораторную СО. Она противоположна с.ц.и. В ЛСО положение частиц определяют относительно покоящейся мишени, на которой рассеиваются другие частицы.

Это интересно! Формула закона полного отражения и преломления света

Полезное видео: инерциальные и неинерциальные системы отсчёта

Относительность движения

По современным представлениям, абсолютной СО не существует. Это значит, что рассматривать движение тел можно только по отношению к другим телам. Не имеет смысла говорить о том, что предмет «двигается вообще». Причина этого — свойства пространства и времени:

Важно! Во времена Ньютона считалось, что можно рассматривать движение относительно абсолютного пространства, позже — относительно эфира в электродинамике Максвелла. Разработанная Эйнштейном теория относительности доказала, что абсолютного начала отсчета быть не может.

Полезное видео: определение координат тела

Вывод

Системы отсчета в физике необходимы, чтобы рассматривать движение тел. Их можно выбирать по-разному, как удобнее для конкретной задачи, так как движение относительно. Для механики важны инерциальные СО — те, которые движутся равномерно и прямолинейно относительно других тел.

Источник

Инерциальные системы отсчета.

Инерциальными системами отсчета называют такие системы, относительно которых все тела, не испытывающие действия сил, движутся равномерно и прямолинейно.

Если какая-либо система отсчета движется относительно инерциальной системы поступательно, но не прямолинейно и равномерно, а с ускорением или же вращаясь, то такая система не может быть инерциальной и закон инерции в ней не выполняется.

Во всех инерциальных системах отсчета все механические и физические процессы протекают совершенно одинаково (при одинаковых условиях).

Согласно принципу относительности, все инерциальные системы отсчета равноправны и все проявления законов физики в них выглядят одинаково, а записи этих законов в разных инерциальных системах отсчета имеют одинаковую форму.

Если в изотропном пространстве существует хотя бы одна инерциальная система отсчета, приходим к выводу, что существует бесконечное множество таких систем, движущихся друг относительно друга поступательно, равномерно и прямолинейно. Если инерциальные системы отсчета существуют, то пространство однородно и изотропно, а время – однородно.

Законы Ньютона и другие законы динамики выполняются только в инерциальных системах отсчета.

Рассмотрим пример инерциальной и неинерциальной систем. Возьмем тележку, на которой находятся два шарика. Один из них лежит на горизонтальной поверхности, а другой подвешен на нити. Сначала тележка движется относительно Земли прямолинейно и равномерно (а). Силы, действующие на каждый шарик по вертикали, уравновешены, а по горизонтали на шарики никакие силы не действуют (силу сопротивления воздуха можно проигнорировать).

При любой скорости движения тележки относительно земли (υ₁, υ₂, υ₃ и т.д.) шарики будут находиться в покое относительно тележки, главное, чтобы скорость была постоянной.

Однако, когда тележка наедет на песчаную насыпь (б), ее скорость начнет быстро уменьшаться, в результате чего тележка остановится. Во время торможения тележки оба шарика придут в движение – изменят свою скорость относительно тележки, хотя их никакие силы не толкают.

В этом примере первой (условно неподвижной) системой отсчета является Земля. Вторая система отсчета, движущаяся относительно первой – тележка. Пока тележка двигалась равномерно и прямолинейно, шарики находились в покое относительно тележки, т. е. выполнялся закон инерции. Как только тележка стала тормозить, т. е. начала двигаться с ускорением относительно инерциальной (первой) системы отсчета, закон инерции перестал выполняться.

Строго инерциальной системы отсчета нет. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом, по отношению к которому изучается различных объектов. Все реальные тела движутся с каким-либо ускорением, следовательно любая реальная система отсчета может рассматриваться в качестве инерциальной лишь приближенно.

Инерциальной системой с очень высокой степенью точности считается гелиоцентрическая система, связанная с центром Солнца и координатными осями, направленными на три далекие звезды. Эту систему используют в задачах небесной механики и космонавтики. В большинстве технических задач инерциальной системой отсчета считают любую систему, жестко связанную с землей (или любым телом, которое покоится или движется прямолинейно и равномерно относительно поверхности Земли).

Источник