Что такое скаляр и вектор
Скаляры и векторы: что это такое
В физике используется много различных математических величин. Например, ускорение, скорость, сила, работа, мощность и так далее. Ученые делят эти величины на два типа: «скалярные» и «векторные». Что же означают эти типы и чем они отличаются?
Скаляр – это величина, которая описывается только значением. Значение этой величины выражает только число. Примеры скалярных величин: скорость, объем, масса, температура, мощность, энергия, время и т.д. Более о скорости читайте в учебнике по физике за 7 класс В.Г. Баряхтяра.
Вектор – это величина, которая имеет как значение, так и направление. Векторные величины важны при изучении движения. Некоторые примеры векторных величин: сила, скорость, ускорение, перемещение и импульс.
Вектор имеет и направление, и значение, а скаляр имеет только значение. Вы можете сказать, является ли величина вектором, просто если поймете, имеет ли эта величина направление.
Как нарисовать вектор?
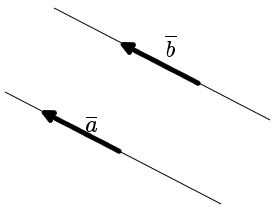
Вектор нарисован в виде стрелки с головой и хвостом. Величину вектора часто описывают длиной стрелки. Стрелка указывает в направлении вектора.
Векторы обычно пишутся в виде жирных букв. Они также могут быть написаны в виде стрелки над буквой.
Пример вопросов: скаляр или вектор?
1) Футболист бежал со скоростью 15 км в час по направлению к концу зоны.
Это вектор, так как он представляет и значение (15 км/ч) и направление (по направлению к концу зоны).
2) Температура помещения составляет 15 градусов по Цельсию.
Это скаляр, направления нет.
3) Автомобиль разогнался на север со скоростью 4 м/с2 (четыре метра в секунду в квадрате).
Это вектор, поскольку он имеет как направление, так и величину. Мы также знаем, что ускорение – это векторная величина.
Знакомимся с вектором
Основы линейной алгебры для тех, кого это миновало в универе.
Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.
Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.
⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.
Линейная алгебра
Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.
Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.
Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.
В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.
Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.
Что такое вектор
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.
Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве
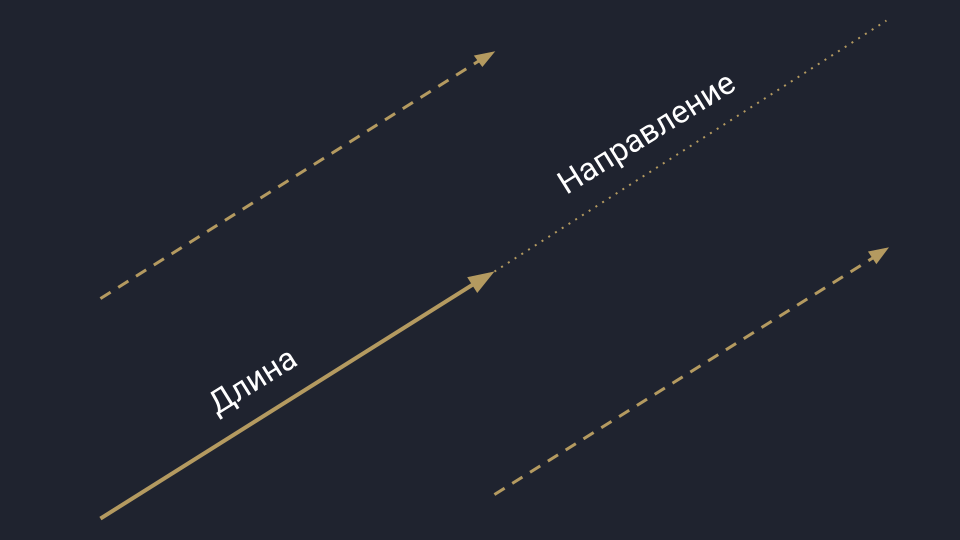
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.
Аналитическое представление вектора: данные можно перевести в числа
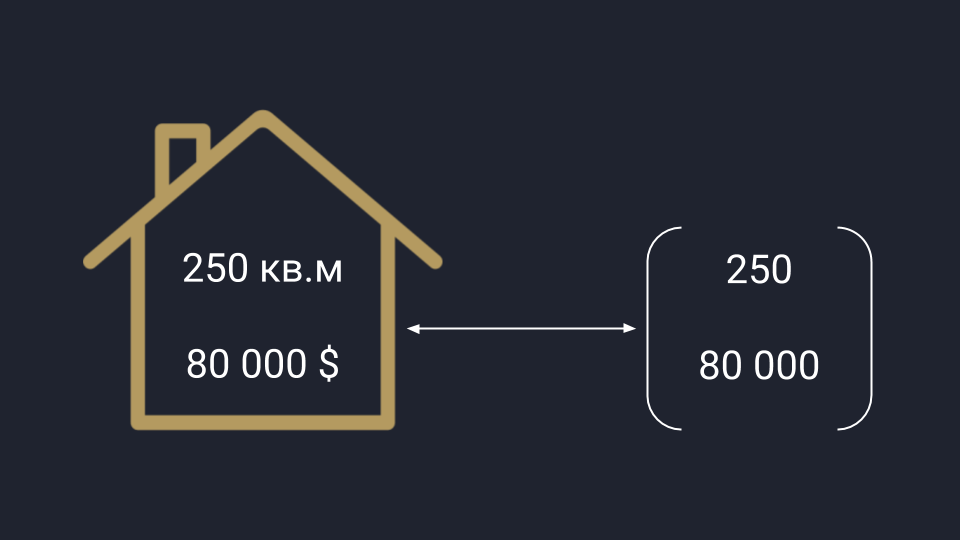
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.
Математическое представление вектора: данные можно перевести в числа или график
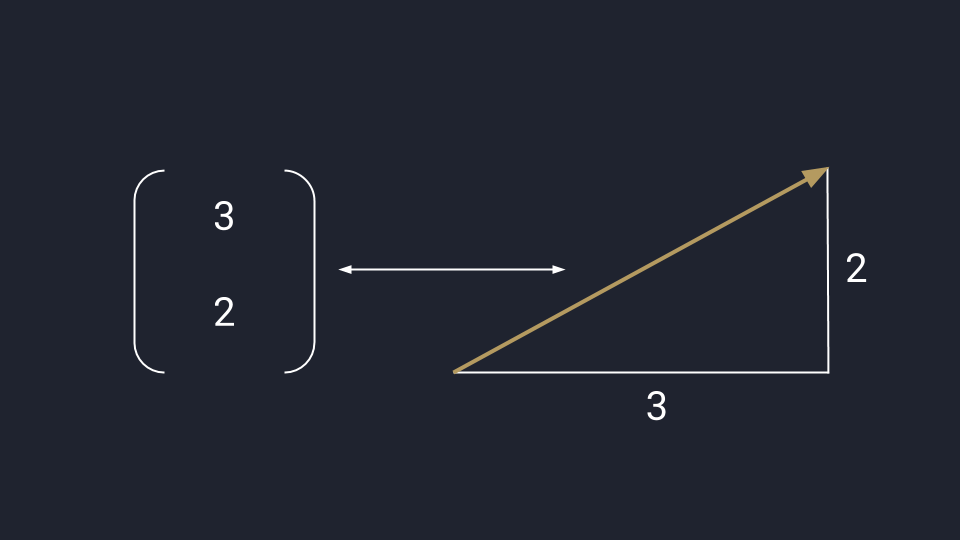
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.
Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат
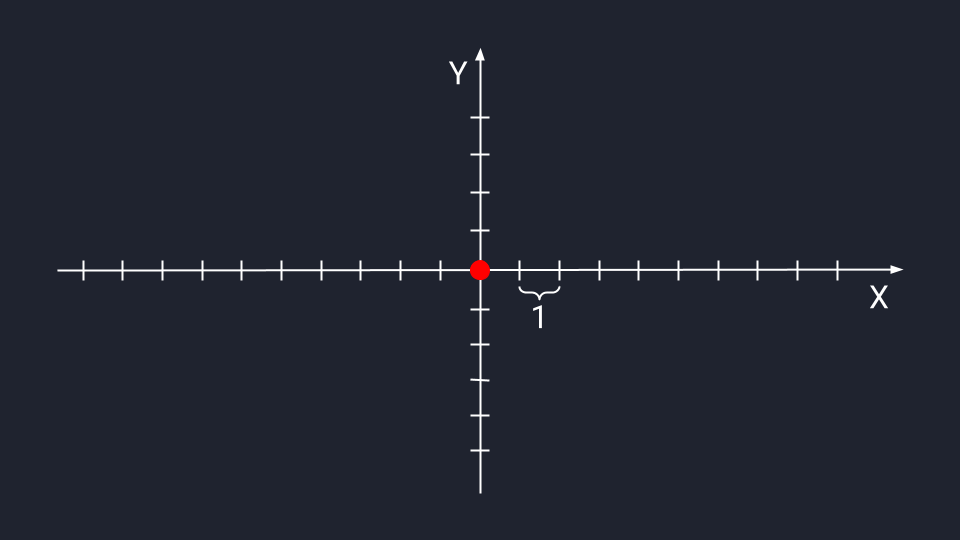
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.
Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.
Как записывать
Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.
Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.
Способы записи вектора
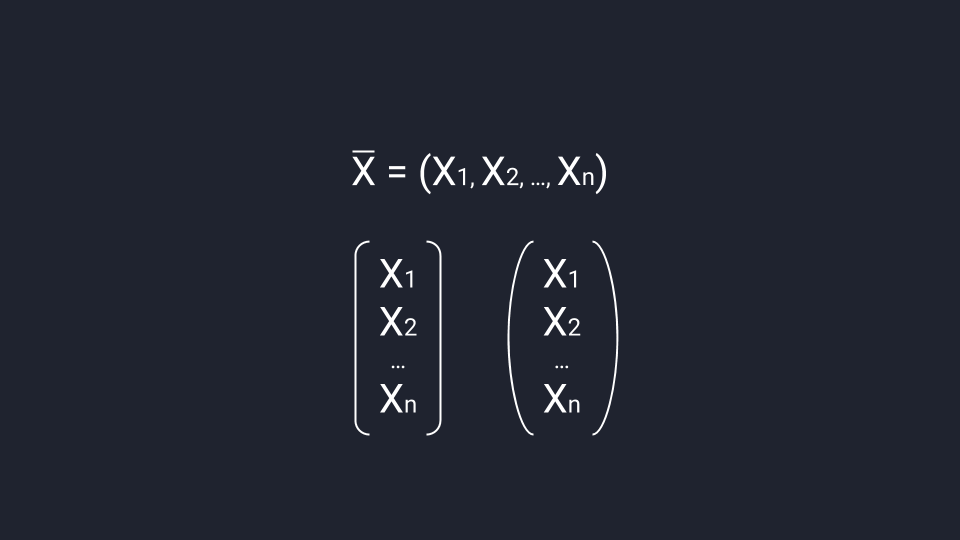
Скаляр
Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.
Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.
Как изображать
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.
Графическое представление скаляра. Записывается в круглых скобках
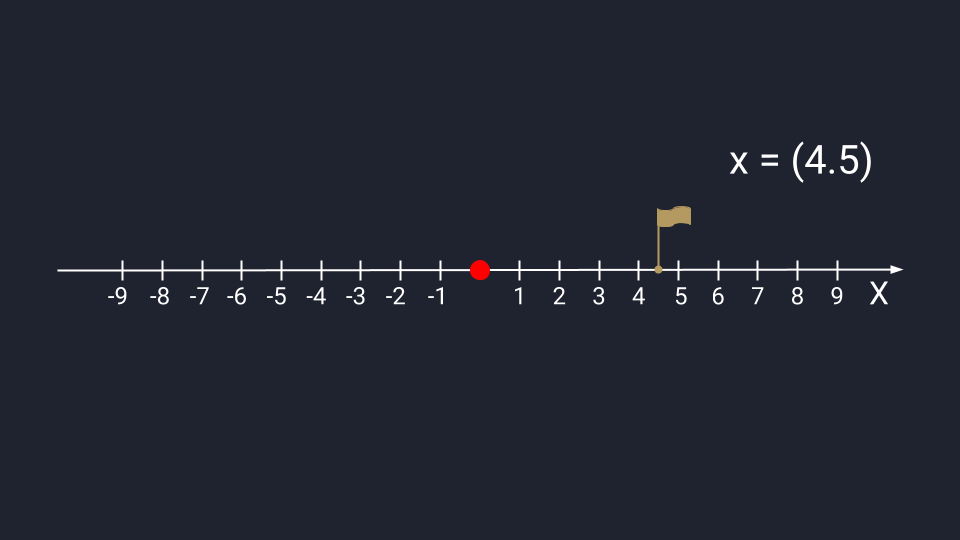
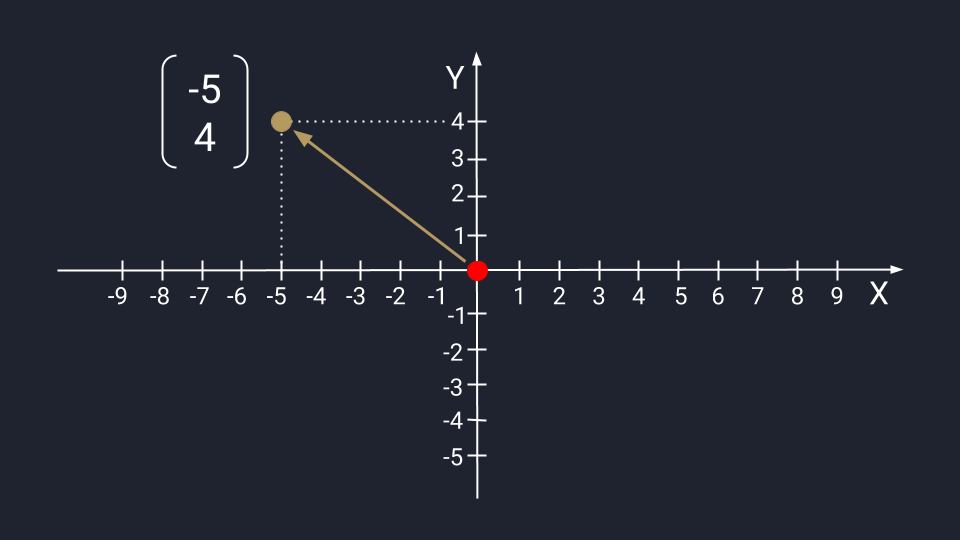
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.
Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.
Графическое представление числового вектора в двух измерениях
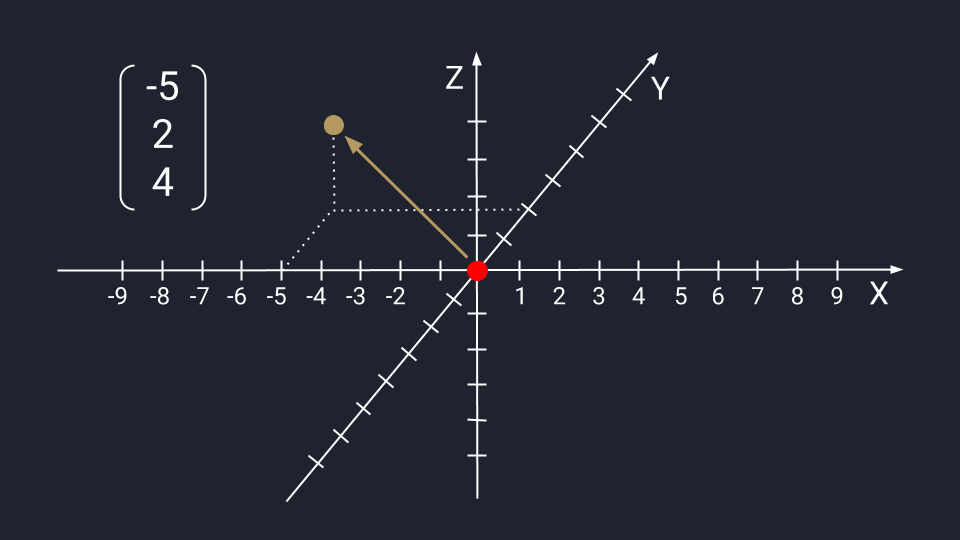
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.
Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.
Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.
Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.
И зачем нам это всё
Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:
Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.
И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.
Что дальше
В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.
Два вида физических величин: скалярные величины и векторные величины
«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.
Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:
Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что
Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.
А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.
Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.
Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.
Какие из представленных на рисунках величин являются скалярными, а какие — векторными?
Что такое скаляр и вектор
В физике существуют скалярные величины (скаляры) и векторные величины (векторы). Хотя, правильнее в последнем случае все-таки говорить векторная величина, часто говорят, например, «вектор скорости».
Чтобы совсем запутаться, рекомендую обратиться к Википедии: https://ru.wikipedia.org/wiki/Векторная_величина.
Для нас важно понять два момента:
1) Примерами скаляров являются: длина, площадь, время, масса, плотность, температура и т.п.
Для наших задач достаточно понимания скаляра, как величины (числа с размерностью) без направления.
2) Под вектором мы будем понимать направленный отрезок. То есть три числа (мы ведь живем в трехмерном пространстве), которые преобразуются по определенным правилам при переходе от одной системы координат к другой.
Попробуем обойтись без математических формул этих правил. Просто представим в нашем трехмерном пространстве направленный отрезок. Некую стрелку, которая, для простоты, неподвижна, неизменна, и имеет направление от одного конца к другому. Или даже представим, что у нас есть определенная операция перемещения в пространстве. У нее есть величина (расстояние перемещения по прямой из начальной точки в конечную) и направление.
И представим систему координат (например, прямоугольную), которая неподвижна относительно нас, и начало отсчета которой совпадает с началом нашего направленного отрезка.
Отлично! Тогда координаты «заостренного» конца нашего «направленного» отрезка с началом в точке (0,0,0) в этой системе координат будут выражаться тремя числами (Ах, Аy, Аz). Будет ли эта тройка чисел вектором?
Теперь мы берем и поворачиваем произвольно нашу систему координат (но пока не сдвигаем начало координат). Тогда в новой системе координат координаты нашего вектора будут (Аx’, Аy’, Аz’). Заметьте, сам наш вектор (направленный отрезок в трехмерном пространстве) не изменился. Как бы мы не вращали систему координат, тройка чисел будет меняться, но вектор (в смысле направленного отрезка) останется на своем месте. Он смотрит в одну и ту же «точку вселенной». О как! И длина его не меняется из-за вращения системы координат.
А теперь вывод. То, что важно для физики!
Формулы можно посмотреть у Фейнмана или еще где-нибудь. Они пока для понимания не столь важны. А важно следующее!
Теперь посмотрим, что есть что.
Путь вектор или скаляр? Скаляр. Почему?
Далее сами перебираем физические величины и определяем, что есть скаляр, а что вектор!
Что такое скаляр и вектор
Для математического изучения скалярных и векторных величин отвлекаются от их конкретного содержания 
вводят отвлеченные понятия скаляра и вектора.
Определение. Скаляром называется всякое действительное число. Вектором называется направленный прямолинейный отрезок.
Направление вектора фиксируется том, что одна его конечная точка считается началом, а вторая — концом. В соответствии с этим считается, что вектор направлен от своего начала к своему концу. На чертеже вектор изображается стрелкой (рис. 1).
В векторном исчислении скаляры и векторы рассматриваются как особого рода алгебраические величины, над которыми производятся алгебраические операции.
Эти операции отражают характерные зависимости, которые существуют между различными скалярными и векторными величииами в геометрии и в различных отделах физики. Изучение этих операций и составляет предмет векторной алгебры.
И векторной алгебре всякая скалярная величин а изображается скаляром, выражающим ее меру при выбранной единице измерения. Всякая векторная величина изображается вектором, который имеет то же направление, что и данная величина, и содержит столько единиц длины, сколько она содержит своих единил измерения. Таким образом, скаляры и векторы в векторной алгебре представляют собой абстрактные математические понятия, при помощи которых изображаются конкретные скалярные и векторные величины, когда мы отвлекаемся от их конкретного содержания, сохраняя лишь их числовые меры и направления.
В векторной алгебре, как и в обычной алгебре, скаляры обозначаются буквами или записываются при помощи цифр:
Векторы, в отличие от скаляров, обозначаются буквами полужирного шрифта:
Часто вектор обозначают парой букв с общей стрелкой над ними: 
При этом первая буква А обозначает начало вектора, а вторая В — его конец (рис. 2). В этом случае говорят та кто, что вектор 
соединяет точку А с точкой В и что вектор А В исходит из точки А.
В векторной алгебре приходится рассматривать также и нулевой вектор. Нулевым вектором является точка. Направление нулевого вектора считается неопределенным. Нулевой вектор обозначается числом нуль, набранным полужирным шрифтом.