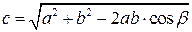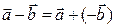Что такое скалярная и векторная
Два вида физических величин: скалярные величины и векторные величины
«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.
Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:
Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что
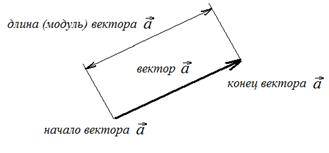
Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.
А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.
Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.
Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.
Какие из представленных на рисунках величин являются скалярными, а какие — векторными?
Что такое скалярная и векторная
В физике существуют скалярные величины (скаляры) и векторные величины (векторы). Хотя, правильнее в последнем случае все-таки говорить векторная величина, часто говорят, например, «вектор скорости».
Чтобы совсем запутаться, рекомендую обратиться к Википедии: https://ru.wikipedia.org/wiki/Векторная_величина.
Для нас важно понять два момента:
1) Примерами скаляров являются: длина, площадь, время, масса, плотность, температура и т.п.
Для наших задач достаточно понимания скаляра, как величины (числа с размерностью) без направления.
2) Под вектором мы будем понимать направленный отрезок. То есть три числа (мы ведь живем в трехмерном пространстве), которые преобразуются по определенным правилам при переходе от одной системы координат к другой.
Попробуем обойтись без математических формул этих правил. Просто представим в нашем трехмерном пространстве направленный отрезок. Некую стрелку, которая, для простоты, неподвижна, неизменна, и имеет направление от одного конца к другому. Или даже представим, что у нас есть определенная операция перемещения в пространстве. У нее есть величина (расстояние перемещения по прямой из начальной точки в конечную) и направление.
И представим систему координат (например, прямоугольную), которая неподвижна относительно нас, и начало отсчета которой совпадает с началом нашего направленного отрезка.
Отлично! Тогда координаты «заостренного» конца нашего «направленного» отрезка с началом в точке (0,0,0) в этой системе координат будут выражаться тремя числами (Ах, Аy, Аz). Будет ли эта тройка чисел вектором?
Теперь мы берем и поворачиваем произвольно нашу систему координат (но пока не сдвигаем начало координат). Тогда в новой системе координат координаты нашего вектора будут (Аx’, Аy’, Аz’). Заметьте, сам наш вектор (направленный отрезок в трехмерном пространстве) не изменился. Как бы мы не вращали систему координат, тройка чисел будет меняться, но вектор (в смысле направленного отрезка) останется на своем месте. Он смотрит в одну и ту же «точку вселенной». О как! И длина его не меняется из-за вращения системы координат.
А теперь вывод. То, что важно для физики!
Формулы можно посмотреть у Фейнмана или еще где-нибудь. Они пока для понимания не столь важны. А важно следующее!
Теперь посмотрим, что есть что.
Путь вектор или скаляр? Скаляр. Почему?
Далее сами перебираем физические величины и определяем, что есть скаляр, а что вектор!
Скалярные и векторные величины



Скалярная величина – это физическая величина, которая имеет только одну характеристику – численное значение.
Скалярная величина может быть положительной или отрицательной.
Примеры скалярных величин: температура, масса, объем, время, плотность. Математические действия со скалярными величинами – это алгебраические действия.

1) численное значение, которое всегда положительно (модуль вектора);
Примеры векторных физических величин: скорость, ускорение, сила.
Векторная величина обозначается латинской буквой и стрелкой над этой буквой. Например:
— вектор скорости обозначается символом 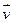
— вектор ускорения обозначается символом 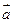
— вектор силы обозначается символом 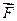
Модуль вектора обозначается так:
На рисунке (графически) вектор изображается направленным отрезком прямой линии. Модуль вектора равен длине направленного отрезка в заданном масштабе.
Действия с векторами
Математические действия с векторными величинами – это геометрические действия.
Сравнение векторов
Равные векторы. Два вектора равны, если они имеют:
Противоположные векторы. Два вектора противоположны, если они имеют:
Сложение векторов
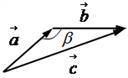
Мы можем сложить два вектора геометрически по правилу параллелограмма и по правилу треугольника.
Пусть заданы два вектора 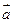
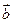
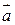
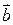
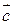
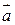
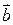
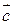
Правило параллелограмма для сложения двух векторов:
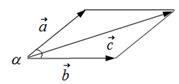
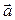
2. Нарисуем вектор 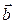
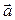
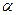
3. Через конец вектора 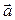
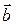
4. Через конец вектора 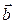
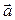
Мы построили параллелограмм. Стороны этого параллелограмма – составляющие векторы 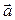
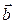
5. Проведем диагональ параллелограмма из общей точки начала вектора 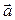
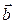
6. Модуль результирующего вектора 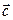
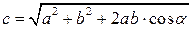
начало вектора 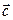
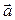
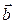
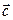
Правило треугольника для сложения двух векторов:
1. Нарисуем составляющие векторы 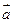
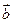
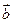
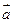
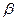
2. Результирующий вектор 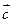
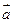
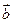
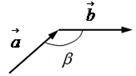
3. Модуль результирующего вектора находим по формуле:
Вычитание векторов
Вычитание векторов – это действие, обратное сложению:
Найти разность вектора 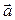
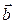
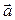
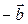
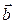
Разница между скалярным и векторным
Главное отличие
Основное различие между скаляром и вектором состоит в том, что скаляр известен как величина, которая включает единственную величину и не имеет направления, тогда как вектор известен как физическая величина, которая состоит из направления и величины.
Скаляр против вектора
Скаляр содержит только величину и не имеет направления; с другой стороны, вектор также содержит как величину, так и направление. Вектор состоит из единственного измерения и считается одномерным; Напротив, вектор содержит множество измерений, поэтому он считается многомерным.
Скалярная величина изменяется, когда происходит изменение ее величины; с другой стороны, векторная величина меняется, когда изменяется величина или направление. Стандартные правила алгебры применимы в случае скаляра; в то же время в векторной алгебре соблюдаются различные наборы алгебраических правил, известных как векторная алгебра.
Одна скалярная величина может быть разделена с другой скалярной величиной; с другой стороны, одну векторную величину нельзя разделить с другой векторной величиной. Сравнение двух скалярных чисел относительно просто; напротив, корреляция между двумя векторными величинами сравнительно сложна.
Скаляр может быть представлен единицей и величиной (числом); с другой стороны, векторная величина может быть представлена единицей и величиной (числом), направлением с помощью ограничения единицы измерения или с помощью стрелки вверху. Символ скаляра — это символ количества; однако, напротив, символ вектора — это символ количества и знак стрелки вверху.
Некоторыми примерами скалярной величины являются энергия, масса, длина, температура и плотность, а некоторыми случаями вектора являются ускорение, вес, смещение, сила и скорость.
Сравнительная таблица
| Скалярный | Вектор |
| Физическая величина, не содержащая какого-либо направления и состоящая из единственной величины, известна как скаляр. | Значение физической величины, состоящей из направления и величины, известно как вектор. |
| Имея в виду | |
| Он содержит только величину и не имеет направления. | Он также содержит как величину, так и направление. |
| Размерные величины | |
| Состоят из единственного измерения и считаются одномерными. | Он содержит много измерений, поэтому считается многомерным. |
| Изменение количества означает | |
| Меняется, когда происходит изменение его величины. | Он чередуется, когда изменяется величина или направление. |
| Правила алгебры | |
| В этом случае применимы общие правила алгебры. | В этом случае используется другой набор алгебраических правил, известный как векторная алгебра. |
| Разделение | |
| Одна скалярная величина может быть разделена на другую скалярную величину. | Одна векторная величина не может быть разделена на другую векторную величину. |
| Сравнение двух величин | |
| Сравнение двух скалярных величин относительно просто. | Контраст между двумя векторными величинами сравнительно сложен. |
| Представлена | |
| Он может быть представлен как единицей измерения, так и величиной (числом). | Он может быть представлен единицей измерения и величиной (числом), направлением, используя колпачок единицы измерения или стрелку вверху. |
| Символы | |
| Символ скаляра — это символ количества. | Символ вектора — это символ количества и знак стрелки вверху. |
| Разрешить в направлениях | |
| Его нельзя разрешить ни в каком направлении, потому что он состоит из одного и того же значения, независимо от направления. | Его можно разрешить в любом направлении, используя синус или косинус смежных углов. |
| Математическая операция | |
| Математическая операция, которая происходит между двумя скалярными величинами, всегда приводит к скаляру; однако, если скалярная величина работает с любой векторной величиной, то результатом будет вектор. | Математическая операция между двумя или многими векторами может дать вектор или скалярную величину, например, умножение двух векторов на точки дает скаляр. Напротив, перекрестное умножение, вычитание или суммирование двух векторов всегда приводит к вектору. |
| Примеры | |
| Некоторые примеры скалярных величин: энергия, масса, длина, температура и плотность. | Некоторые примеры Vector: ускорение, вес, смещение, сила и скорость. |
Что такое скаляр?
Вид физической величины, в которой размерность определяется только величиной величины, а не направлением, тогда это называется скаляром. Скалярная величина никогда не состоит из направления, потому что она касается только величины объекта.
В сценарии скаляра, когда замечается какое-либо изменение количества, это происходит только из-за изменения его величины. Как правило, скалярные величины подчиняются общим законам алгебраических правил, и поэтому их можно легко алгебраически вычесть, сложить, разделить или умножить, как и стандартные числа, хотя скалярные величины должны содержать точные единицы.
Что такое вектор?
Величина, в которой размер определяется направлением и величиной объекта, обычно называется вектором. Когда две величины имеют одинаковую величину и одинаковое направление, тогда эти две величины будут называться векторными величинами.
Когда чередование происходит как по величине, так и по направлению, это приведет к изменению векторной величины. Векторная величина обычно не следует основным правилам алгебры, потому что направление связано с векторной величиной, вместо этого следует алгебраическим векторным законам. Некоторые примеры Vector: ускорение, вес, смещение, сила и скорость.
Ключевые отличия
Заключение
Из приведенного выше обсуждения делается вывод, что если величина состоит только из величины, то она будет известна как скалярная величина; Напротив, если величина состоит как из направления, так и из величины, то это будет векторная величина.
Разница между векторной и скалярной величиной
В физике выделяют 2 категории величин — векторные и скалярные. Что представляют собой те и другие?
Что представляет собой векторная величина?
Под векторной принято понимать величину, имеющую 2 основные характеристики:
Так, два вектора признаются равными, если модули, а также направления обоих совпадают. Записывается рассматриваемая величина чаще всего как буква, над которой прорисовывается стрелка.
В числе самых распространенных величин соответствующего типа — скорость, сила, а также, например, ускорение.
С геометрической точки зрения вектор может представлять собой направленный отрезок, длина которого соотносится с его модулем.
Если рассматривать векторную величину обособленно от направления, то ее принципиально можно измерить. Правда, это будет, так или иначе, частичная характеристика соответствующей величины. Полная — достигается только в случае ее дополнения параметрами направленного отрезка.
Что представляет собой скалярная величина?
Под скалярной принято понимать величину, которая имеет только 1 характеристику, а именно — численное значение. При этом рассматриваемая величина может принимать положительное или же отрицательное значение.
К распространенным скалярным величинам можно отнести массу, частоту, напряжение, температуру. С ними возможно производить различные математические действия — сложение, вычитание, умножение, деление.
Направление (как характеристика) не свойственно для скалярных величин.
Сравнение
Главное отличие векторной величины от скалярной заключается в том, что у первой ключевые характеристики — модуль и направление, у второй — численное значение. Стоит отметить, что векторную величину, как и скалярную, принципиально можно измерить, правда, в этом случае ее характеристики определятся только частично, поскольку будет недоставать направления.
Определив,в чем разница между векторной и скалярной величиной, отразим выводы в небольшой таблице.