Что такое скалярное число
Скаляры и векторы: что это такое
В физике используется много различных математических величин. Например, ускорение, скорость, сила, работа, мощность и так далее. Ученые делят эти величины на два типа: «скалярные» и «векторные». Что же означают эти типы и чем они отличаются?
Скаляр – это величина, которая описывается только значением. Значение этой величины выражает только число. Примеры скалярных величин: скорость, объем, масса, температура, мощность, энергия, время и т.д. Более о скорости читайте в учебнике по физике за 7 класс В.Г. Баряхтяра.
Вектор – это величина, которая имеет как значение, так и направление. Векторные величины важны при изучении движения. Некоторые примеры векторных величин: сила, скорость, ускорение, перемещение и импульс.
Вектор имеет и направление, и значение, а скаляр имеет только значение. Вы можете сказать, является ли величина вектором, просто если поймете, имеет ли эта величина направление.
Как нарисовать вектор?
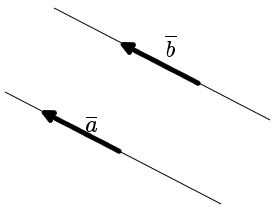
Вектор нарисован в виде стрелки с головой и хвостом. Величину вектора часто описывают длиной стрелки. Стрелка указывает в направлении вектора.
Векторы обычно пишутся в виде жирных букв. Они также могут быть написаны в виде стрелки над буквой.
Пример вопросов: скаляр или вектор?
1) Футболист бежал со скоростью 15 км в час по направлению к концу зоны.
Это вектор, так как он представляет и значение (15 км/ч) и направление (по направлению к концу зоны).
2) Температура помещения составляет 15 градусов по Цельсию.
Это скаляр, направления нет.
3) Автомобиль разогнался на север со скоростью 4 м/с2 (четыре метра в секунду в квадрате).
Это вектор, поскольку он имеет как направление, так и величину. Мы также знаем, что ускорение – это векторная величина.
Скаляр
Скаляр (от лат. scalaris — ступенчатый) — величина (возможно переменная, то есть функция), каждое значение которой может быть выражено одним числом (чаще всего подразумевается вещественное число).
При смене системы координат скаляр остаётся неизменным (инвариантным), в отличие, например, от компонентов вектора, которые могут быть разными у одного и того же вектора в разных системах координат.
Содержание
Примеры
Важно заметить, что понятие скаляра довольно сильно связано с контекстом. Так, в общепринятом контексте современной физики часть приведённых величин скалярными не являются. [1]
Ошибочные примеры
То же касается координаты тензора любой другой валентности (кроме нулевой).
Ещё одним примером величины, не являющейся, строго говоря, скаляром, является псевдоскаляр (хотя на практике иногда, исходя из соображений удобства или краткости, разграничения между скалярами и псевдоскалярами могут и не проводить, если это не существенно для изложения).
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Скаляр» в других словарях:
скаляр — а, м. scalaire <лат. scalaris ступенчатый < scalae лестница. Величина, в противоположность вектору, определяемая числовым значением без указания направления. БАС 1. Скалярный ая, ое. Скалярные величины. Уш. 1940: Лекс. СИС 1937: скаля/ры;… … Исторический словарь галлицизмов русского языка
скаляр — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] скаляр Величина, каждое значение которой может быть выражено одним (как правило, действительным) числом; по… … Справочник технического переводчика
СКАЛЯР — (от латинского scalaris ступенчатый) (скалярная величина), величина, каждое значение которой (в отличие от вектора) может быть выражено одним (действительным) числом, вследствие чего совокупность значений скаляра можно изобразить на линейной… … Современная энциклопедия
СКАЛЯР — (от лат. scalaris ступенчатый) (скалярная величина) величина, каждое значение которой (в отличие от вектора) может быть выражено одним (действительным) числом, вследствие чего совокупность значений скаляра можно изобразить на линейной шкале… … Большой Энциклопедический словарь
СКАЛЯР — СКАЛЯР, математическое число, имеющее только величину, в отличие от ВЕКТОРА, который имеет еще и направление. Масса и энергия являются скалярными величинами, тогда как вес и сила представлены векторными величинами … Научно-технический энциклопедический словарь
СКАЛЯР — величина, значение которой характеризуется действительным числом (без учета направления). Напр., температура, концентрация и т.п. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
Скаляр — [scalar] величина, каждое значение которой может быть выражено одним (как правило, действительным) числом; по отношению к вектору, который можно рассматривать как многомерную величину, С. величина одномерная. Скалярная (числовая) функция одной… … Экономико-математический словарь
СКАЛЯР — величина, каждое значение которой может быть выражено одним действительным числом без учёта направления млн. другой какой либо оценки в выбранной системе единиц, напр. длина, площадь, объём, плотность, работа, температура и др … Большая политехническая энциклопедия
скаляр — а; м. [лат. scalaris ступенчатый] Матем. Величина, имеющая только числовое значение. ◁ Скалярный, ая, ое. С ые величины. * * * скаляр (от лат. scalaris ступенчатый) (скалярная величина), величина, каждое значение которой (в отличие от вектора)… … Энциклопедический словарь
Два вида физических величин: скалярные величины и векторные величины
«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.
Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:
Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что
Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.
А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.
Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.
Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.
Какие из представленных на рисунках величин являются скалярными, а какие — векторными?
Что это значит, когда данные скалярные?
Я не знаю, что именно означает скаляр, но я пытаюсь понять, правильно ли я думаю об этом. Относится ли скаляр к произвольности, когда тип данных может быть любого типа, или система не может заранее знать, что это за данные.
Дополнительная мнемоника к великому ответу Карла Билефельдта:
Простой способ думать об этом, «это может быть в масштабе?»
Целое число может быть в масштабе.
Реальное число может быть в масштабе.
Символ, логическое значение или десятичная дробь с фиксированной точностью могут быть в масштабе. Даже строка может быть в масштабе (мы используем такие в сортировке).
Строка базы данных не может быть в масштабе. Комплексное число не может быть в масштабе. Объект, представляющий сообщение электронной почты, не может быть в масштабе. Массив, вектор или матрица не могут быть в масштабе.
Как и в случае со многими терминами в вычислительной технике; Происхождение слова связано с более физическими свойствами. Термин Скалярный является относительно старым в вычислительной технике. Его определение в наши дни менее строгое. Когда вы храните данные в памяти компьютера, эти данные могут помещаться в один адрес (1 байт *) или нет. Когда это было, это называлось скалярным, когда это не называлось составным. Главным образом потому, что процессоры могут обрабатывать только один адрес / часть данных (= 1 байт) за раз. Как заявлено @Karl Bielefeldt; термин действительно был взят из алгебры.
Мы называем строку строкой, потому что это строка символов. Символ является / был скаляром, а строка является / была составной. Хранение 1 части данных (данных) по нескольким адресам несколько размыло линию. Подумайте об этом так: когда процессор мог обрабатывать данные в одной инструкции, это было скалярно.
(* Я говорю 1 байт, чтобы прояснить ситуацию, но технически я говорю о тех днях, когда 6 бит чаще использовались, например, на перфокартах, а затем на магнитных полосах)
Отказ от ответственности: я не могу найти какие-либо ссылки на это в Интернете, я получил информацию в школе и из старых книг, среди которых (я думаю): математические таблицы и другие пособия для вычислений с 1944 года. При этом моя память не то, что раньше, так что если кто-то может изменить / подтвердить или опровергнуть мой ответ, было бы неплохо.
Однако обратите внимание, что большой очень сложный тип данных такого рода, который также может быть сведен и представлен в 8-битных байтах компьютерной памяти, также может быть представлен как одно очень длинное / большое двоичное скалярное число. Тьюринг использовал эту технику для представления целых компьютерных программ как одного скалярного числа.
Скалярное произведение векторов: свойства, примеры вычисления, физический смысл
Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.
При умножении вектора самого на себя, получим квадрат его дины:
Скалярное умножение вектора самого на себя называют скалярным квадратом.
Вычисляется по формуле:
Сформулируем определение произведения для двух векторов:
Скалярное произведение двух векторов a → на b → называют произведение длины вектора a → на проекцию b → на направление a → или произведение длины b → на проекцию a → соответственно.
Скалярное произведение в координатах
Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.
для трехмерного пространства применимо выражение:
Фактически это является третьим определением скалярного произведения.
Следует отложить векторы
– соответственно для векторов трехмерного пространства.
Скалярное произведение и его свойства
Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.
Дистрибутивность справедлива для любых чисел:
Скалярное произведение с примерами и решениями
Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:
Рассмотрим некоторые примеры решения.
Длина a → равна 3, длина b → равна 7. Найти скалярное произведение, если угол имеет 60 градусов.
По условию имеем все данные, поэтому вычисляем по формуле:
В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:
Для начала вычисляются координаты векторов, так как по условию даны координаты точек:
Подставив в формулу с использованием координат, получим:
Выносим коэффициент за знак произведения и получим:
По свойству коммутативности преобразуем:
Теперь применим формулу для скалярного произведения с заданным по условию углом:
Если имеется числовая проекция.
Подставив в формулу, получим выражение:
Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.
Из формулы видно, что необходимо найти сумму произведений координат:
Физический смысл скалярного произведения
Механика рассматривает приложение скалярного произведения.
При работе А с постоянной силой F → перемещаемое тело из точки M в N можно найти произведение длин векторов F → и M N → с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения: