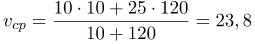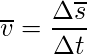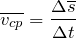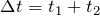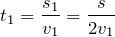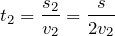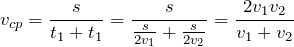Что такое скорость в физике определение кратко

Понятие и основные термины

Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.

Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.

Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

Угловая скорость

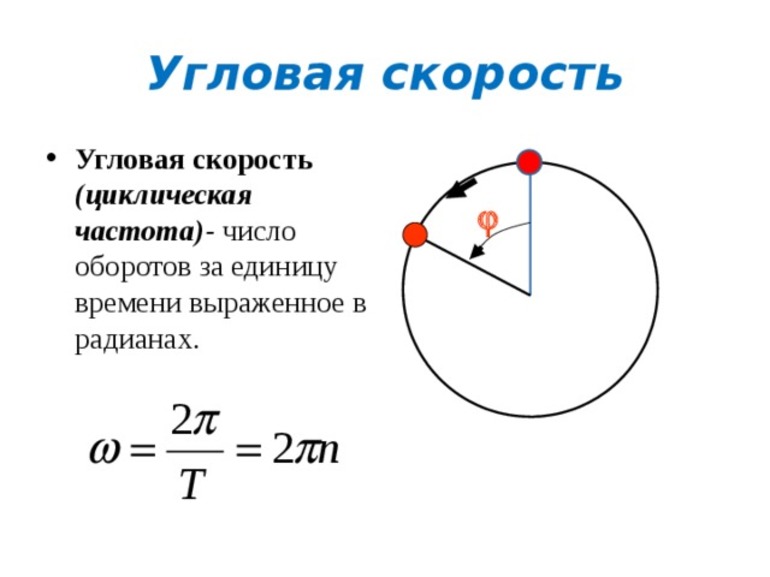
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Источник

Виды скорости в физике и методы их вычисления

Скорость в физике — что это такое

Скорость — векторная физическая величина, которая характеризуется направлением и быстротой перемещения материальной точки.

В физике понятие скорости встречается в разделе «Кинематика», в котором дается описание механического движения, а это основа изучения скорости как векторной физической величины.

Скорость может характеризоваться быстротой перемещения не только материальной точки, но и еще элементарных частиц и волн.

Скорость звука — это величина, которая показывает, на какое расстояние может распространиться звуковая волна за единицу времени.

Скорость света — абсолютная величина, которая показывает скорость распространения электромагнитных волн.

Виды скорости в физике, основные характеристики

В физике существуют такие виды скорости, как: начальная скорость, равномерная скорость, средняя скорость, мгновенная скорость.

Как писалось выше, скорость равна отношению пути S ко времени t.

Формулы скорости при движении разных видов

ϑ н — начальная скорость;

ϑ 0 — конечная скорость;

Примеры задач с решением

На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?

Решение:

Скорость — это расстояние, пройденное телом за единицу времени. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения.

Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это и есть скорость движения.

ϑ = 180 3 = 60 к м ч

Ответ: скорость автомобиля составляет 60 км/ч.

Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа — со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

В условии сказано о трех участках пути.

ϑ с р = S о б щ t о б щ

ϑ с р = S 1 + S 2 + S 3 t 1 + t 2 + t 3

Участки пути нам не даны, но мы можем без труда их вычислить:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

ϑ с р = 100 + 180 + 160 1 + 2 + 2 / = 440 5 = 88 к м ч

Ответ: средняя скорость составляет 88 км/ч.

Конечная скорость после 2 секунд движения с ускорением 0,2 м/с², равна 3 м/с. Найти начальную скорость.

Ответ: начальная скорость составляет 2,6 м/с.

Источник

СКОРОСТЬ

Измеряют С. обычно в м/с (СИ), см/с (СГС) или в км/ч.

В проекциях на оси координат компоненты С. имеют следующий вид (см.

а) в декартовых координатах х, у, z

б) в цилиндрич. координатах

в) всферич. координатах

Модуль С. в этих случаях равен квадратному корню из суммы квадратовсоответствующих компонент.

Когда говорят о С. произвольно движущегося тела или системы тел, тоимеют в виду С. их центра масс. Это естеств. обобщение С. материальнойточки.

В ньютоновской (нерелятивистской) механике С. точки при переходе отодной инерциальной системы отсчёта К’ к др. системе К преобразуетсяпо закону

В более сложном случае, когда K’-система совершает произвольное движениеотносительно K-системы, С. точки преобразуется по ф-ле

В относительности теории установлен фундам. факт: в природе существуетпредельная С. распространения взаимодействий и сигналов (а значит. и тел).Она равна С. света в вакууме с =2,99792458*10 8 м/с. Лоренца преобразованиями при переходе от K’- к K-системе отсчётаф-лы преобразования компонент С. приобретают более сложный вид:

Смотреть что такое СКОРОСТЬ в других словарях:

СКОРОСТЬ

(la vitesse, die Geschwindigkeit, velocity). — Понятие о С. получается из понятий о средней С. в пути и средней С. перемещения. При рассмотрении движен. смотреть

СКОРОСТЬ

IСко́рость в механике, одна из основных кинематических характеристик движения точки, равная численно при равномерном движении отношению пройденн. смотреть

СКОРОСТЬ

СКОРОСТЬ

скорость ж. 1) Отношение пройденного телом пути к соответствующему промежутку времени. 2) Степень быстроты движения или вращения некоторых машин (автомобиля, мотоцикла, станка и т.п.), зависящая от порядка взаимодействия деталей коробки скоростей. 3) а) Степень быстроты движения, распространения, действия и т.п. б) разг. Поспешность, торопливость.

СКОРОСТЬ

скорость ж.speed; rate; физ., мех. velocity максимальная скорость — maximum / top speed переменная скорость — variable speed развивать, набирать скорос. смотреть

СКОРОСТЬ

СКОРОСТЬ

СКОРОСТЬ

СКОРОСТЬ в механике, одна из осн. кинематич. характеристик движения точки, равная численно при равномерном движении отношению пройденного пути s к пр. смотреть

СКОРОСТЬ

Скорость (la vitesse, die Geschwindigkeit, velocity). — Понятие о С. получается из понятий о средней С. в пути и средней С. перемещения. При рассмотрении движения точки по прямой или данной кривой линии приходится говорить как о длине пути, пройденного точкою в течение какого-либо промежутка времени, так и о перемещении ее в течение того же промежутка; эти величины могут и не быть одинаковы, если движение происходило то в одну, то в другую сторону по пути. Говоря о перемещении, приходится выбрать на пути неподвижную точку как начало считаемых от нее расстояний по кривой или пути и условиться, в которую сторону по кривой считать расстояния от этого начала положительными; тогда в противоположную сторону придется считать расстояния отрицательными длинами по кривой. Пусть s₁ и s₂ суть расстояния движущейся точки в моменты времени t₁ и t₂, при чем t₂ больше t₁. Разность (s₂—s₁) называется перемещением точки за промежуток времени t₂—t₁; оно может быть положительным или отрицательным. Если в течение этого промежутка времени направление движения точки не переменялось в противоположное, то длина пути будет равна величине расстояния по кривой между положениями точки в моменты t₁ и t₂ и эту величину мы всегда будем рассматривать как положительную, хотя бы расстояние (s₂—s₁) и было отрицательным. Если в течение этого промежутка времени направление движения менялось один или несколько раз в противоположное, то длиною пути будем называть сумму положительно взятых длин между положением в момент t₁ и положением в момент первой перемены направления, положением в этот момент и положением в момент второй перемены направления и т. д. В этом случае полная длина пути не будет равна величине расстояния (s₂—s₁), даже если бы последнее было положительным. Отношение величины (s₂—s₁) к величине (t₂—t₁ ) называется среднею С. перемещения за этот промежуток времени, а отношение длины пути к величине (t₂—t₁) называется среднею С. в пути за тот же промежуток времени. Последняя всегда положительная, а первая может быть и отрицательною. Если в течение рассматриваемого промежутка времени направление движения не менялось, то средняя С. перемещения равняется средней С. в пути, если движение происходило в сторону возрастающих расстояний, или равняется отрицательно взятой средней. С. в пути, если движение совершалось в сторону убывающих расстояний. Равномерным движением называется такое движение, при котором средняя С. одинакова для всяких промежутков времени, больших или сколь угодно малых; при неравномерных движениях величина средней С. для одного и того же промежутка времени различна в различных частях пути и, кроме того, величина эта изменяется при изменении величины промежутка времени. К понятию о скорости в какой-либо момент движения переходят следующим образом. Каково бы ни было движение точки, во всяком случае при всяком движении расстояние s может быть выражено некоторою непрерывною функциею от t. Возьмем произвольный момент t и определим среднюю С. промежутка времени, заключающего этот момент; полученная величина будет изменяться по мере уменьшения выбранного промежутка времени. Предел, к которому будет приближаться средняя С. по мере приближения промежутка времени к нулю, называется С. движения в рассматриваемый момент. В статье Дифференциальное исчисление (см.) говорилось именно об этой величине С. Это есть производная от s = f(t) по t. Величина эта будет положительною, если в момент t точка двигалась в сторону возрастающих s, и она будет отрицательною в случае движения в сторону убывающих s. Предел средней С. в пути, найденный подобным же образом для того же момента t, будет во всяком случае положительною величиною v. Это будет та же самая величина, какую представляет производная от s по t, если движение совершается в сторону возрастающих s; а если движение совершается в сторону убывающих s, то v равна отрицательно взятой производной от s по t. Величина С. в какой-либо момент, как и величина средней С., есть отношение длины ко времени. О единице С. сказано в ст. Абсолютная система единиц (см.). В морской практике употребляется единица С., называемая узлом; это та С., при которой в час проходится итальянская миля, т. е. 1852 метра, поэтому узел равен 0,514 [метр]/[секунда] = 50 [фут]/[полуминута]. С. представляют себе в виде вектора (см.), отложенного от места, занимаемого точкою в пространстве и имеющего направление по касательной к кривой, описываемой точкою, в сторону движения. Длина этого вектора должна так относиться к единице длины, как величина v к единице С. Если положение точки выражается координатами ее x, у, z по отношению к прямоугольным прямолинейным неподвижным осям координат, то координаты движущейся точки должны выражаться непрерывными функциями от t. Проекции С. v на оси координата выражаются производными от этих функций по времени, а именно: vcos(vX)= dx/dt vcos(vY)= dy/dt vcos (v Z) = dz/dt О годографе С. точки cм соотв. ст. Об угловой С. см. Вращательное движение. Относительно величин скоростей, встречающихся в разных случаях движения, см. брошюру: «Таблицы встречаемых в технике С., выраженных в метра в секунду», инж.-технол. П. Киреева, 3 изд., 1881, СПб. Д. Б.

СКОРОСТЬ

05.01.18 скорость (обработки) [rate]: Число радиочастотных меток, обрабатываемых за единицу времени, включая модулированный и постоянный сигнал. Прим. смотреть

Источник

Скорость движения

Скорость является одной из основных характеристик механического движения. Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.

Единицей измерения скорости в системе СИ является м/с.

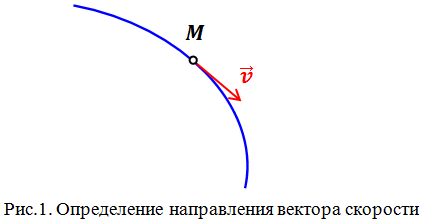
Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по траектории движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).

К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.

Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).

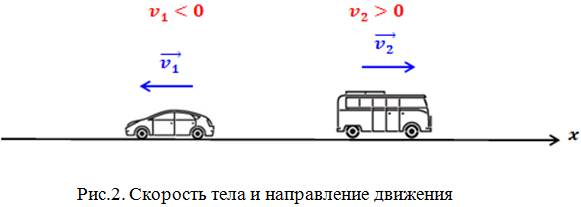
Отрицательная скорость

Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.

Равномерное и неравномерно движение

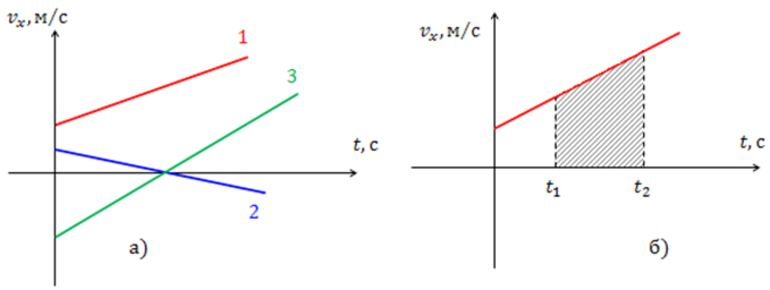
В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.

В случае неравномерного движения говорят о средней скорости:

Примеры решения задач по теме «Скорость»

Задание	Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля.
Решение	Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей.

Воспользуемся определением средней скорости:

Так как предполагается прямолинейное равномерное движение, знаки векторов можно опустить.

Время, потраченное автомобилем на прохождение всего отрезка пути:

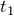
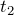
где — время, затраченное на прохождение первой половины пути, а — время, затраченное на прохождение второй половины пути.

Суммарное перемещение равно расстоянию между населенными пунктами, т.е. .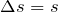

Подставив эти соотношения в формулу для средней скорости, получим:

Переведем скорости на отдельных участках в систему СИ:

км/ч м/с

км/ч м/с

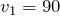
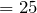
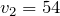
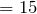
Тогда средняя скорость автомобиля:

(м/с)

ОтветСредняя скорость автомобиля равна 18,8 м/с

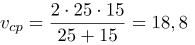
Задание	Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 25 м/с. Определить среднюю скорость автомобиля.
Решение	Сделаем рисунок.

Также как и в предыдущей задаче, знаки векторов в формуле опускаем. предполагая равномерное прямолинейное движение.

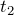
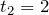
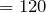
Время в системе СИ измеряется в секундах, переводим значение времени в систему СИ:

мин сек

Средняя скорость автомобиля:

(м/с)

Источник