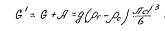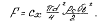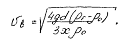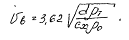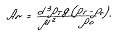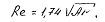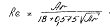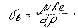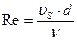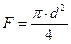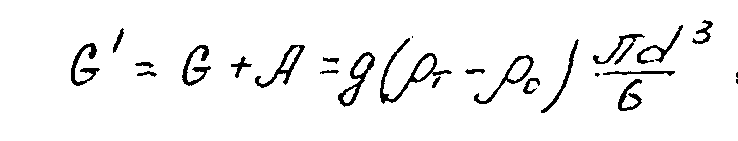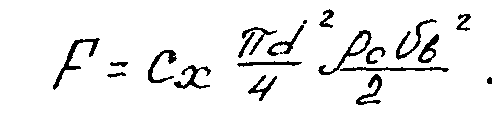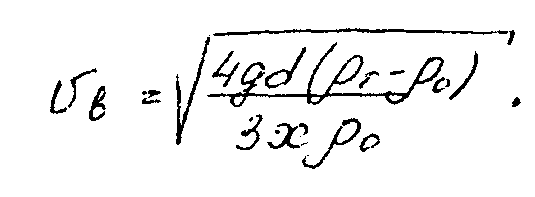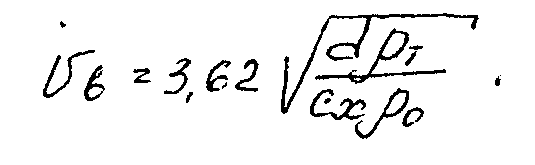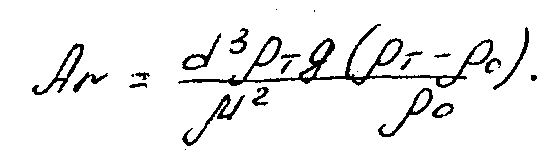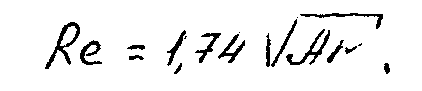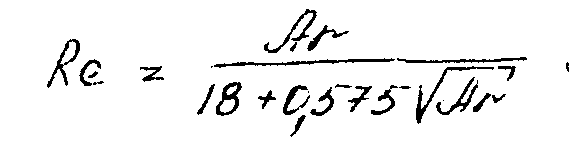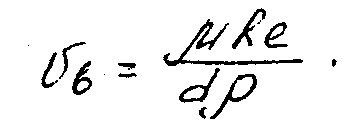Что такое скорость витания

Скорость витания, методы ее расчета, практическое значение.

При свободном падении твердой частицы в жидкой или газовой среде, находящейся в покое, только в первый момент наблюдается ускоренное движение; в дальнейшем возникающая сила сопротивления уравновешивается действием силы тяжести и частица падает равномерно, с постоянной скоростью. Эта скорость называется гидравлической крупностью. Это понятие имеет большое значение при изучении процессов взвешивания и отстаивания в жидкости, а также для расчета трубопроводов для гидротранспорта частиц.

При изучении аналогичных процессов в воздушной среде используется понятие скорости витания. Под последней понимают скорость восходящего потока воздуха (в вертикальной трубе), при которой твердые частицы, находящиеся в этом потоке, будут совершать колебательные движения приблизительно на одном уровне (как бы витать), т.е. будут находиться во взвешенном состоянии. Иначе говоря, это понятие эквивалентно гидравлической крупности применительно к воздушной среде.

Выведем формулу скорости витания частицы шарообразной формы.

Таким образом, сила падения

Сила сопротивления при падении частицы в воздухе

Так как эти силы уравновешиваются при равномерном падении, то 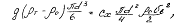откуда

Поскольку плотность воздуха r0 значительно меньше плотности rт транспортируемого материала, разность rт-r0 без большой ошибки можно заменить на rт. Тогда формула для скорости витания шарообразной частицы принимает вид

Итак, зная коэффициент сопротивления частицы cx, нетрудно по формуле определить скорость витания. Так как значения cx в свою очередь, зависят от скорости, задача решается методом подбора.

Для частиц определенной формы коэффициент лобового сопротивления зависит только от числа Рейнольдса, поэтому уравнение равномерного осаждения (всплывания) твердых частиц можно представить в виде зависимости числа Рейнольдса от критерия Архимеда:

При Re 83000

Для расчетов может быть использована и единая интерполяционная зависимость, связывающая критерии Re и Ar для всех режимов осаждения:

Таким образом, рассчитав критерий Ar, определяют по его значению область, в которой происходит осаждение. Вычисляют, пользуясь одним из уравнений, отвечающим этой области, значение Re и находят по нему скорость осаждения

Для обеспечения пневмотранспорта твердых материалов среднюю скорость движения воздуха в трубопроводе берут несколько большей (в зависимости от формы частиц и концентрации материала) скорости витания, определенной для шаровидной частицы по формуле (21).

Понятие скорости витания по существу относится к вертикальным участкам трубопроводов пневмотранспорта. На горизонтальных участках условия для перемещения твердых частиц иные.

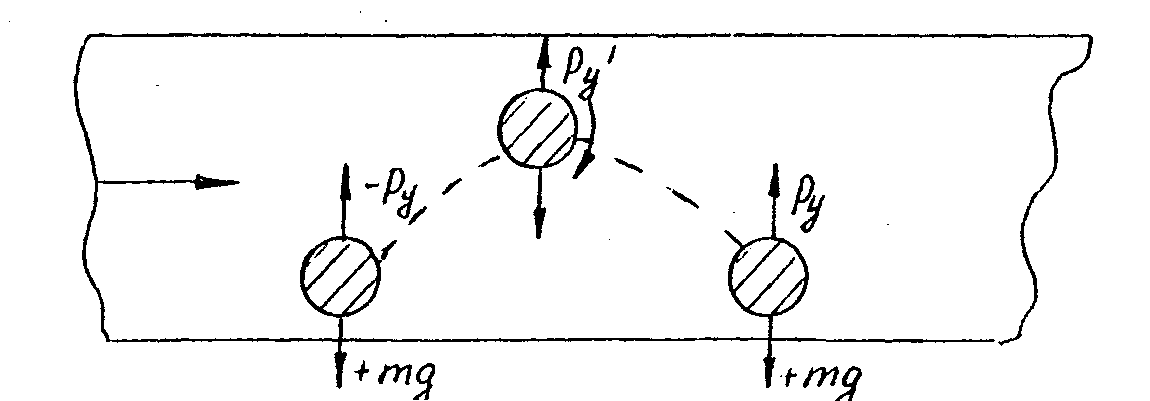
Рассмотрим механизм перемещения твердых частиц в горизонтальной трубе (рис.). Возьмем шаровидную частицу, расположенную на дне трубы. При обтекании шара, как и при обтекании цилиндра, вверху частицы вследствие увеличения скорости образуется область пониженного давления и возникает подъемная сила P, которая при достаточной скорости поднимает частицу. Сила сопротивления F перемещает частицу в направлении движения воздуха в трубе, а сама частица начинает вращаться (в данном случае по часовой стрелке) в результате эффекта вязкостного трения. В дальнейшем, когда частица поднялась, действие подъемной силы Р прекращается,| но вращение частицы благодаря инерции и наличию поперечного градиента осредненных скоростей сохраняется. Последнее образует циркуляцию и соответствующую ей подъемную силу Pу (эффект Магнуса). Эта сила, как правило, недостаточна для поддержания частицы во взвешенном состоянии. Поэтому частица, описав некоторую траекторию, падает на дно трубы и описанное явление повторяется.

Если весьма увеличить скорость течения воздуха, то можно добиться того, что твердые частицы будут перемещаться в горизонтальном трубопроводе, не падая на дно, т.е. будут находиться во взвешенном состоянии. Такая способность турбулентного потока объясняется наличием в нем поперечных пульсаций. Однако осуществлять пневмотранспорт таким образом вследствие большой разницы плотностей воздуха и материала экономически нецелесообразно, а в некоторых случаях даже невозможно. Наоборот, гидротранспорт, где разность плотностей материала и воды в большинстве случаев незначительна, осуществляется при таких скоростях течения воды, когда частицы находятся во взвешенном состоянии.

Скорость веяния по абсолютной величине мало отличается от скорости витания. Поэтому на практике расчет пневмотранспорта ведут по скорости витания.

Рис. Механизм перемещения твердых частиц потоком воздуха в горизонтальном направлении

Дата добавления: 2016-06-29 ; просмотров: 9433 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Скорость витания твердой частицы в потоке воздуха

Рассмотрим свободное падение твердых частицы в воздухе. Пусть твердая частица, имеющая массу m (рис.46) свободно без толчка падает из т. О, которую принимаем за начало координат. Ось У по которой осуществляется падение частицы направим вертикально вниз. Под действием силы тяжести равной P=m∙g частица будет падать, оставаясь, все время на оси У.

Рис.46

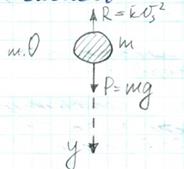
В первый начальный момент времени частица будет падать под действием ускорения свободного падения (g=9,81м/с 2 ), но т.к. воздух оказывает сопротивление движению частицы через некоторое время частица будет падать с определенной постоянной скоростью без ускорения. Т.о. скорость падения частицы в вязкой среде, которой является воздух не может беспредельно возрастать, а с течением некоторого времени достигает своего наибольшего значения υ_S, которая сохраняет во все последующее время падения. Если твердую частицу поместить в восходящий воздушный поток, частица зависнет в нем, т.е. будет витать.

Средняя скорость восходящего воздушного потока, при которой частица ни будет иметь вертикального перемещения, а будет находится во взвешенном состоянии называется скоростью витания.

Скорость витания частицы равна постоянной скорости падения частицы в неподвижном воздухе.

Таким образом, на твердую частицу действуют две силы:

1) сила тяжести; 2) сила сопротивления воздуха R. R может быть записана как:

, (79)

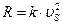
где υ_S – скорость восходящего потока воздуха

к – коэффициент пропорциональности.

При достижении падающей частицей постоянной скорости сила тяжести равна силе сопротивления Р=R, тогда:

(80)

(81)

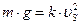
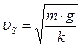
Сопротивление среды движущемуся в ней воздуху можно записать в следующем виде:

(82)

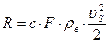
где с – коэффициент пропорциональности, с=ƒ(Re)

F – площадь проекции тела на плоскость перпендикулярную вектору скорости, м 2

ρ_в – плотность среды (воздуха).

Следовательно, из выражений (79) и (82) заключаем, что коэффициент пропорциональности к может быть записан в виде:

(83)

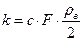
А скорость падения частицы в воздухе с учетом выражения (83) будет:

(84)

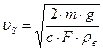
Коэффициент пропорциональности с в выражении (84)может быть определен по формуле Клячко:

(85)

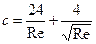
С достаточной для практике точностью (85) можно записать:

(85а)

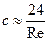
Подставляя выражение (85а) в функцию (84) при развернутом виде Re:

ν – коэффициент кинематической вязкости воздуха, м 2 /с

Численное значение скорости υ_S можем определить:

(86)

(87)

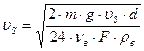
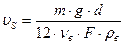
Для частицы, имеющей форму близкую к шару, масса частицы:

(88)

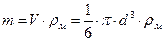
Следовательно, выражение (88) можно записать в виде:

(89)

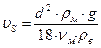
где ρ_м – плотность материала частицы.

Формула (89) справедлива для частиц, имеющих форму шара с размером до 100 мк. Такая пыль, например, выделяется при обработке древесины на шлифовальных станках. Все же другие отходы и материалы, которые могут транспортироваться системами пневмотранспорта, имеют большие размеры и по форме отличаются от формы шара. Поэтому скорость витания этих частиц в инженерной практике определяется по эмпирическим формулам, которые справедливы для частиц определенной формы данного материала. Процесс пневматического транспортирования частиц в вертикальных воздуховодах возможет, только если скорость воздушного потока превышает максимальное значение скоростей витания частиц.

Дата добавления: 2015-08-11 ; просмотров: 5526 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Скорость витания, методы ее расчета, практическое значение.

При свободном падении твердой частицы в жидкой или газовой среде, находящейся в покое, только в первый момент наблюдается ускоренное движение; в дальнейшем возникающая сила сопротивления уравновешивается действием силы тяжести и частица падает равномерно, с постоянной скоростью. Эта скорость называется гидравлической крупностью. Это понятие имеет большое значение при изучении процессов взвешивания и отстаивания в жидкости, а также для расчета трубопроводов для гидротранспорта частиц.

При изучении аналогичных процессов в воздушной среде используется понятие скорости витания. Под последней понимают скорость восходящего потока воздуха (в вертикальной трубе), при которой твердые частицы, находящиеся в этом потоке, будут совершать колебательные движения приблизительно на одном уровне (как бы витать), т.е. будут находиться во взвешенном состоянии. Иначе говоря, это понятие эквивалентно гидравлической крупности применительно к воздушной среде.

Выведем формулу скорости витания частицы шарообразной формы.

Таким образом, сила падения

Сила сопротивления при падении частицы в воздухе

Так как эти силы уравновешиваются при равномерном падении, то 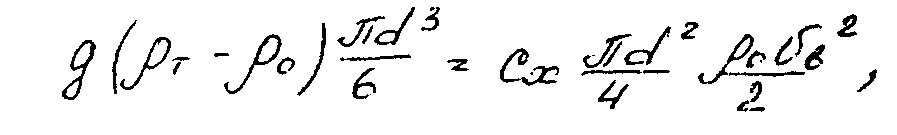откуда

Поскольку плотность воздуха r0 значительно меньше плотности rт транспортируемого материала, разность rт-r0 без большой ошибки можно заменить на rт. Тогда формула для скорости витания шарообразной частицы принимает вид

Итак, зная коэффициент сопротивления частицы cx, нетрудно по формуле определить скорость витания. Так как значения cx в свою очередь, зависят от скорости, задача решается методом подбора.

Для частиц определенной формы коэффициент лобового сопротивления зависит только от числа Рейнольдса, поэтому уравнение равномерного осаждения (всплывания) твердых частиц можно представить в виде зависимости числа Рейнольдса от критерия Архимеда:

При Re 83000

Для расчетов может быть использована и единая интерполяционная зависимость, связывающая критерии Re и Ar для всех режимов осаждения:

Таким образом, рассчитав критерий Ar, определяют по его значению область, в которой происходит осаждение. Вычисляют, пользуясь одним из уравнений, отвечающим этой области, значение Re и находят по нему скорость осаждения

Для обеспечения пневмотранспорта твердых материалов среднюю скорость движения воздуха в трубопроводе берут несколько большей (в зависимости от формы частиц и концентрации материала) скорости витания, определенной для шаровидной частицы по формуле (21).

Понятие скорости витания по существу относится к вертикальным участкам трубопроводов пневмотранспорта. На горизонтальных участках условия для перемещения твердых частиц иные.

Рассмотрим механизм перемещения твердых частиц в горизонтальной трубе (рис.). Возьмем шаровидную частицу, расположенную на дне трубы. При обтекании шара, как и при обтекании цилиндра, вверху частицы вследствие увеличения скорости образуется область пониженного давления и возникает подъемная сила P, которая при достаточной скорости поднимает частицу. Сила сопротивления F перемещает частицу в направлении движения воздуха в трубе, а сама частица начинает вращаться (в данном случае по часовой стрелке) в результате эффекта вязкостного трения. В дальнейшем, когда частица поднялась, действие подъемной силы Р прекращается,| но вращение частицы благодаря инерции и наличию поперечного градиента осредненных скоростей сохраняется. Последнее образует циркуляцию и соответствующую ей подъемную силу Pу (эффект Магнуса). Эта сила, как правило, недостаточна для поддержания частицы во взвешенном состоянии. Поэтому частица, описав некоторую траекторию, падает на дно трубы и описанное явление повторяется.

Если весьма увеличить скорость течения воздуха, то можно добиться того, что твердые частицы будут перемещаться в горизонтальном трубопроводе, не падая на дно, т.е. будут находиться во взвешенном состоянии. Такая способность турбулентного потока объясняется наличием в нем поперечных пульсаций. Однако осуществлять пневмотранспорт таким образом вследствие большой разницы плотностей воздуха и материала экономически нецелесообразно, а в некоторых случаях даже невозможно. Наоборот, гидротранспорт, где разность плотностей материала и воды в большинстве случаев незначительна, осуществляется при таких скоростях течения воды, когда частицы находятся во взвешенном состоянии.

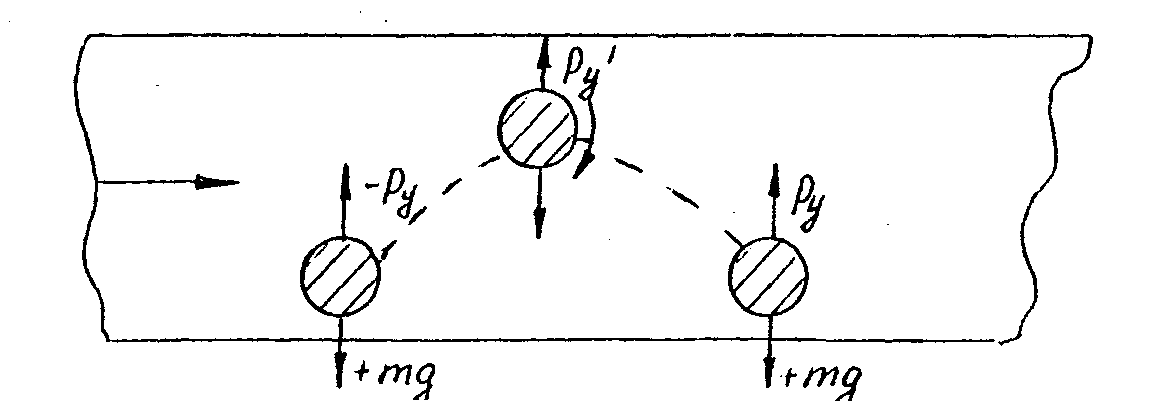
Скорость веяния по абсолютной величине мало отличается от скорости витания. Поэтому на практике расчет пневмотранспорта ведут по скорости витания.

Рис. Механизм перемещения твердых частиц потоком воздуха в горизонтальном направлении

Дата добавления: 2018-02-15 ; просмотров: 694 ; Мы поможем в написании вашей работы!

Источник

Расчет скорости витания и дисперсности частиц

Для эффективного улавливания пылевых выбросов необходимо создать та­кую скорость во всасывающем отверстии местного отсоса, при которой пыле­вая частица не будет оседать и будет двигаться вместе с газовым потоком. Скорость вертикального потока воздуха, при которой частица удерживается во взвешенном состоянии, называется скоростью витания.

Исходные данные приведены в таблице

Расчет скорости витания может быть произведен двумя способами:

· по расчетным формулам;

Для частиц диаметром до 300 мкм скорость витания расчитывается по формуле

При определении v_s по графику учитывается диаметр, удельный вес частицы, а также значение вязкости воздуха при заданной температуре. Для учета истинного значения вязкости воздуха полученное значение v_s умножается на поправочный коэффициент К, который определяется с помощью следующих данных

Расчет дисперсности частиц

Для выбора способа очистки воздуха и типа аппарата необходимо знать группу дисперсности пыли. Дисперсный состав пыли может быть выражен следующими способами:

· в виде графика распределения массы пыли по размерам частиц;

· в виде таблицы «полных проходов» или «частных остатков» частиц разных размеров в процентах от общей массы пыли (например, от 0 до 5, до 10, до 20 мкм и т.д. или от 0 до 5, от 5 до 10, от 10 до 20 и т.д.);

· в виде таблицы скоростей витания.

Группу дисперсности пыли определяют при помощи номограммы, представленной на рис. на основании данных о фракционном составе пыли. Номограмма разбита на пять зон, которые соответствуют классификационным группам пыли. Для определения группы заданной пыли на номограмму наносят точки, соответствующие содержанию отдельных фракций пыли. Соединяя эти точки, получают прямую или ломаную линию, расположение которой в той или иной зоне номограммы обозначает принадлежность пыли к классификационной группе, соответствующей этой зоне. Если линия дисперсности, нанесенная на номограмму, не укладывается в пределах одной зоны, пересекая границу смежных зон, пыль следует относить к классификационной группе верхней зоны.

Исходные данные приведены в таблице

Размер частиц, мкм % по массе для варианта	80
0	4	6	10	24	28	28
1	5	9	18	28	30	10
2	7	8	12	26	22	15
3	6	9	24	28	27	6
4	8	12	18	29	21	12
5	5	9	18	28	30	10
6	8	12	18	29	21	12
7	7	8	12	26	22	15
8	4	6	10	24	28	28
9	6	9	24	28	27	6

Расчет фильтровальных аппаратов

Расчет фильтров сводится к определению площади фильтро­вальных элементов, гидравлического сопротивления фильтроваль­ного элемента и фильтра, продолжи­тельности работы фильтра до регенерации фильтровальных элементов и мощности привода вен­тилятора.

Исходными данными для расчета являются:

· объем газа О, по­ступающего на очистку, м з /ч;

· допустимая удельная газовая нагрузка (скорость фильтрации), определяемая из условия дости­жения максимальной эффективности очистки газа и величины до­пустимого гидравлического сопротивления на фильтро­вальном эле­менте,

· входная концентрация пыли, мг/м 3 ;

· дисперс­ность пыли, характеризуемая значением d₅₀, мкм, и среднеквад­ратичным отклонением s;

· требуемая эффективность очистки газо­вого потока от пыли.

Исходные данные для расчета приведены в таблице

Поверхность F (м 2 ) фильтрующего элемента определяется по формуле:

Рекомендуемые значения удельной газовой нагрузки q зависят от свойств улавливаемой пыли, структуры фильтроваль­ного материала, тре­буемой эффективности очистки и др. С достаточной для практи­ческих расчетов точностью удельную газовую нагрузку для рукав­ных фильтров оп­ределяют из выражения :

где q_n—нормативная газовая нагрузка, зависящая от вида пыли.

Коэффициент c₁, учитывающий особенности регенерации фильт­ровальных элементов, для регенерации фильтроэлементов из тка­ни импульс­ной продувкой сжатым газом равен 1; для рукавов из нетканых материалов 1,05—1,1.

Коэффициент c₂, учитывающий влияние входной концентра­ции пыли на удель­ную газовую нагрузку, определяют по следую­щим данным:

с вх, г/м 3	2	5	10	20	40	60	80	100
c2	1,15	1,04	1,00	0,96	0,90	0,87	0,85	0,83

Коэффициент с₃, учитывающий влияние дисперсного состава пыли, определяют по данным, приведенным ниже:

d50, мкм	100
с3	0,7-0,9	0,9	1,0	1,1	1,2-1,4

Коэффициент с₄, учитывающий влияние температуры очищаемого газа, находят по данным, приведенным ниже:

t, °С	20	40	60	80	100	120	140	160
с4	1	0,9	0,84	0,78	0,73	0,72	0,72	0,7

Постоянную составляющую гидравлического сопротивле­ния фильтро­вальной перегородки определяют по фор­муле

Переменная составляющая гидравлического сопротивления фильтровальной пе­регородки определяется толщиной и структурой пылевого слоя, образующегося на перегородке, а также измене­нием порового пространства перегородки за счет заби­вания пор частицами пыли. Этот процесс зависит от времени фильтрования и описывается за­висимостью

где k_c—параметр сопротивления слоя пыли, зависящий от меди­анного размера час­тиц, коэффициента сопротивления x_n слоя пы­ли и насыпной плотности r_н слоя, t- продолжительность фильтровального цикла, с.

Гидравлическое сопротивление Dр₂ корпуса фильтра определя­ется суммой по­терь давления, возникающих при движении потока воздуха в газоходах, местных сопротивлениях, дроссельных за­слонках и т. п. Для расчета гидравлического сопро­тивления ис­пользуют зависимость

где x_к – коэффициент гидравлического сопротивления, V_вх – скорость движения газового потока, м/с.

Мощность электродвигателя вентилятора, необходимого для транспортирования газов через пылеулавливающий аппарат, оп­ределяют по формуле

при этом ко­эффициент запаса мощно­сти k_зап принимается равным 1,1—1,15; КПД передачи мощно­сти от электродвигателя к вентилятору h₁ для клиноременной передачи 0,92—0,95; КПД вентилятора h₂ = 0,65—0,8.

Расчет циклонов

Для расчетов циклона НИИОГАЗа необходимы следующие исходные дан­ные:

· объем очищаемого газа Q, м 3 /с;

· плотность газа при рабочих условиях r_г, кг/м 3 ;

· вязкость газа при рабочей температуре m, Па-с;

· дисперсный состав пыли d₅₀ и lg s_ч;

· входная концентрация пыли с_вх г/м 3 ;

· плотность частиц пыли r_ч, кг/м 3 ;

· требуемая эффективность очистки газа h.

Расчет циклонов ведут методом последовательных приближений в следую­щем порядке.

Исходные данные для расчета приведены в таблице

1. Задавшись типом циклона, определяют оптимальную скорость газа w_оп в сечении циклона диаметром D по следующим данным:

Тип циклона ЦН-24 ЦН-15 ЦН-11 СДК-ЦН-33 СК-ЦН-34 СК-ЦН-34м

2. Вычисляют диаметр циклона D (м) по формуле:

Полученное значение D округляют до ближайшего типового значения внутрен­него диаметра циклона. Если расчетный диаметр циклона превышает его мак­симально допустимое значение, то необходимо применять два или более парал­лельно установленных циклона.

3. По выбранному диаметру циклона находят действительную скорость движения газа в циклоне, м/с:

где n — число циклонов. Дей­ствительная скорость в циклоне не должна отклоняться от оптимальной более чем на 15%.

4. Определяют коэффициент гидравлического сопротивления одиночного циклона

Таблица 31

Значение k₁ для D, мм

150200300450500ЦН-110,940,950,960,991,0ЦН-15, ЦН-240,850,900,931,01,0СДК-ЦН-33, СК-ЦН-34, СК-ЦН-34м1,01,01,01,01,0

5. Гидравлическое сопротивление циклона вычисляют по формуле

6. Эффективность очистки газа в циклоне:

где Ф(х)—табличная функция от параметра х, равного:

Значения d₅₀ t и lgs_ч для каждого типа циклона приведены в таблице:

Таблица

Тип циклона010204080120150ЦН-1110,960,940,920,900,87ЦН-1510,930,920,910,900,870,86ЦН-2410,950,930,920,900,870,86СДК-ЦН-3310,810,7850,780,770,760,745СК-ЦН-3410,980,9470,930,9150,910,90СК-ЦН-34М10,990,970,95———при выхлопе в атмосферупри выхлопе в гидравлическую сетьпри выхлопе в атмосферупри выхлопе в гидравлическую сетьЦН-11245250СДК-ЦН-33520600ЦН-15155163СК-ЦН-3410501150ЦН-247580СК-ЦН-34М—2000

Определив по формуле (**) значение х, находим параметр Ф по данным таблицы ( ):

Таблица

х	-2,70	-2,0	-1,8	-1,6	-1,4	-1,2
Ф(х)	-0,0035	0,0228	0,0359	0,0548	0,0808	0,1151
х	-1,0	-0,8	-0,6	-0,4	-0,2	—
Ф(х)	0,1587	0,2119	0,2743	0,3446	0,4207	—
х	0,0	0,2	0,4	0,6	0,8	1,0
Ф(х)	0,5000	0,5793	0,6554	0,7257	0,7881	0,8413
х	1,2	1,4	1,6	1,8	2,0	2,7
Ф(х)	0,8849	0,9192	0,9452	0,9641	0,9772	0,9965

Затем по формуле (*) определяют расчетное значение эффективности очистки газа циклоном. Если расчетное значение h окажется меньше необходимого по условиям допустимого выброса пыли в атмосферу, то нужно выбрать другой тип циклона с большим значением коэффициента гидравлического сопротивления.

Расчет скрубберов Вентури

Исходные данные для расчета приведены в таблице

Вариант Параметры	0	1	2	3	4	5	6	7	8	9
zсух	0,12	0,14	0,13	0,15	0,12	0,12	0,14	0,13	0,15	0,12
wг, м/с	80	50	60	90	70	50	100	90	70	60
rг, кг/м 3
w вых, м/с	20	16	16	14	12	16	20	18	17	15
w ц, м/с	20	16	16	14	12	16	20	18	17	15
w цф, м/с	2	4	3	4	2	3	4	3	2	4

Размер частиц, мкм % по массе для варианта	8
0	4	6	10	24	28	28
1	5	9	18	28	30	10
2	7	8	12	26	22	15
3	6	9	24	28	27	6
4	8	12	18	29	21	12
5	5	9	18	28	30	10
6	8	12	18	29	21	12
7	7	8	12	26	22	15
8	4	6	10	24	28	28
9	6	9	24	28	27	6

Гидравлическое сопротивление трубы-распылителя, Па, при подаче в нее оро­шающей жидкости удобно рассматривать как сумму слагаемых:

где Dр — гидравлическое сопротивление трубы-распылителя. Па; Dр_г — гидравличе­ское сопротивление трубы-распылителя, обусловленное движением газов (без пода­чи орошения). Па; Dр_ж — гидравлическое сопротивление трубы-распылителя, обуслов­ленное вводом орошающей жидкости. Па.

Гидравлическое сопротивление сухой трубы-распылителя. Па, определяется по формуле

Гидравлическое сопротивление труб-распылителей, Па, обусловленное вводом орошающей жидкости, рассчитывается по формуле

Дата добавления: 2018-05-09 ; просмотров: 2220 ; Мы поможем в написании вашей работы!

Источник