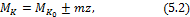Что такое скручивающий и крутящий моменты

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

Источник

Кручение прямого стержня. Скручивающие моменты. Крутящие моменты и их эпюры. Гипотезы при кручении

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

Рис. 1

В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты M_k в поперечных сечениях различных участков вала неодинаковы.

На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.

При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. M_k примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.2).

Рис. 2

При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты М_К связаны дифференциальной зависимостью

из которой вытекает следующая формула:

где 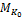– крутящий момент в начале участка.

Согласно формуле (2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (М_К = М_Ко = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре М_К возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.

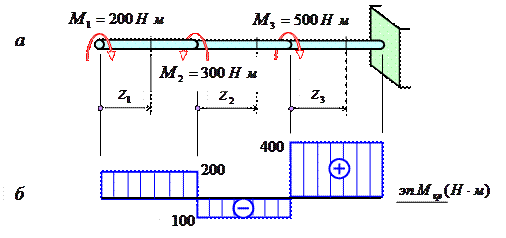
На рис. 4, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.

В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.

Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.

Крутящий момент M_z1 в сечении I численно равен M₁=200 нм и, согласно принятому правилу знаков, положителен.

Крутящий момент M_z2 в сечении II численно равен алгебраической сумме моментов M₁ и M₁, т.е. M_z2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.

Аналогичным образом вычисляется крутящий момент M_z3 в сечении III: M_z3 =200-300+500=400 нм.

Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.4, б показана такая эпюра для стержня, изображенного на рис. 4, а.

Каждая ордината эп. M_k в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.

В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.

Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.

Дата добавления: 2018-04-04 ; просмотров: 1019 ; Мы поможем в написании вашей работы!

Источник

Деформация кручения. Крутящий момент.

Полярный момент сопротивления кручению. Вращающий (скручивающий) момент.

Кручение возникает при действии на брус двух пар сил (см. рис. 228, г), действующих в плоскостях, перпендикулярных оси бруса. Момент такой пары внешних сил называется

Учитывая, что при кручении происходит сдвиг и что поэтому напряжение в каждой точке пропорционально относительной деформации, и сама относительная деформация зависит от расстояния точки до оси бруса (до центра сечения, называемого полюсом), можно с помощью математических преобразований, приравняв сумму моментов внутренних сил относительно продольной оси бруса внешнему моменту (метод сечения), определить величину максимальных касательных напряжений при кручении (вывод справедлив для бруса круглого сечения диаметром d) следующим образом:

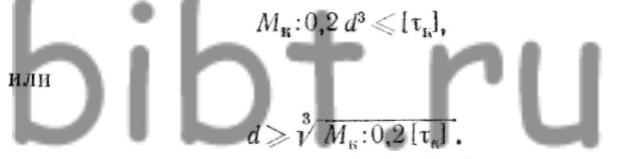
Типовой деталью, испытывающей деформацию кручения, является вал. При проектном расчете на прочность по крутящему моменту и допускаемому напряжению определяют диаметр вала. Исходной является зависимость, в которой в качестве максимальных напряжений используются допускаемые напряжения.

Так как для валов многих машин заранее бывает известен не момент, а передаваемая мощность N и угловая скорость ω вращения вала (или n об/мин), то прежде всего определяют вращающий (скручивающий) момент по формуле M=N:ω, если вместо ω задано n, то ω=πn:30.

Так как М к =М, то далее расчет ведется по вышеприведенной формуле.

При проверочном расчете, как и в случаях других деформаций, определяют действительные напряжения и сравнивают с допускаемыми.

Источник