Что такое слау в математике
Что такое слау в математике
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
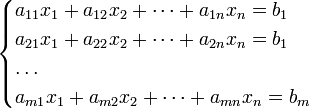 | (1) |
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Содержание
Матричная форма
Система линейных уравнений может быть представлена в матричной форме как:
или, согласно правилу перемножения матриц,
Если к матрице А прибавить столбец свободных членов, то А называется расширенной матрицей.
Методы решения
Прямые (или точные) методы, позволяют найти решение за определенное количество шагов. Итерационные методы, основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений
Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.
Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.
Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему
Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной, если же решений нет – несовместной. Если совместная СЛАУ имеет ровно одно решение, её именуют определённой, если бесконечное множество решений – неопределённой.
Естественно, возникает вопрос том, является ли проверенное решение единственным. Вопрос о количестве решений СЛАУ будет затронут в соответствующей теме.
$$4x_1+2x_2-x_3=4\cdot 0+2\cdot 0-0=0.$$
Подстановка в иные уравнения делается аналогично.
Матричная форма записи систем линейных алгебраических уравнений.
С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:
Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков (см. пример №4).
Чтобы была нагляднее взаимосвязь между матрицей системы и самой системой, я запишу рядом заданную СЛАУ и ее матрицу системы:
Как видите, изменение порядка следования неизвестных равносильно перестановке столбцов матрицы системы. Но каким бы этот порядок расположения неизвестных ни был, он должен совпадать во всех уравнениях заданной СЛАУ.
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Система линейных алгебраических уравнений
В данной публикации мы рассмотрим определение системы линейных алгебраических уравнений (СЛАУ), как она выглядит, какие виды бывают, а также как ее представить в матричной форме, в том числе расширенной.
Определение системы линейных уравнений
Система линейных алгебраических уравнений (или сокращенно “СЛАУ”) – это система, которая в общем виде выглядит так:
Индексы коэффициентов ( aij ) формируются следующим образом:
Виды СЛАУ
В зависимости от количества решений, СЛАУ может быть:
Матричная форма записи системы
СЛАУ можно представить в матричной форме:
Пример
Представим систему уравнений ниже в матричном виде:
Пользуясь формами выше, составляем основную матрицу с коэффициентами, столбцы с неизвестными и свободными членами.
Полная запись заданной системы уравнений в матричном виде:
Расширенная матрица СЛАУ
Для примера выше получается так:

Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений с неизвестными называется система уравнений вида
Систему (5.1) принято записывать в матричной форме. Для этого из коэффициентов системы составляем матрицу системы
свободные члены записываем в столбец свободных членов
а неизвестные — в столбец неизвестных
Матричная запись неоднородной системы уравнений (5.1) имеет вид
Матричную запись (5.3) системы уравнений можно представить в эквивалентной форме
Тогда решение системы представляется столбцом и удовлетворяет равенству
т.е. столбец свободных членов является линейной комбинацией столбцов матрицы системы.
Относительно системы уравнений нас интересуют ответы на следующие вопросы:
1. Совместна система или нет?
2. Если система совместна, то имеет ли она единственное решение или нет?
3. Если решение единственное, то как его найти?
4. Если система имеет бесконечно много решений, то какова структура множества решений?
5. Как в бесконечном множестве решений системы определить одно решение, наилучшее с практической точки зрения?
6. Если система несовместна, то как определить ее приближенное решение?
Правило Крамера
где матрица системы — квадратная n-го порядка:
Ее определитель обозначим
Теорема 5.1 (правило Крамера). Если определитель матрицы системы линейных уравнений с неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам
где — определитель матрицы, полученной из матрицы системы заменой i-го столбца столбцом свободных членов, т.е.
1. На практике при больших правило Крамера не применяется, так как вычисление определителя n-го порядка требует большого числа арифметических операций. Поэтому применяются более экономичные алгоритмы. Обычно, правило Крамера используется, когда нужно найти только несколько неизвестных (например, одну) среди многих. В теоретических исследованиях правило Крамера незаменимо и используется весьма продуктивно.
Пример 5.1. Решить систему линейных уравнений с помощью правила Крамера
Так как определитель отличен от нуля, система имеет единственное решение (см. теорему 5.1). Находим определители и неизвестные
Условие совместности системы линейных уравнений
Рассмотрим систему (5.3) линейных уравнений с неизвестными. Составим блочную матрицу, приписав к матрице справа столбец свободных членов. Получим расширенную матрицу системы :
Эта матрица содержит всю информацию о системе уравнений, за исключением обозначений неизвестных.
Замечание 5.2. Теорема Кронекера-Капелли дает лишь критерий существования решения системы, но не указывает способа отыскания этого решения.
Пример 5.2. Определить, имеет ли система уравнений решения
Решение. Составим матрицу системы и расширенную матрицу системы
Ранг матрицы равен 2, так как она имеет не равные нулю миноры второго порядка и третья строка этой матрицы равна сумме первых двух строк. Следовательно, третью строку можно вычеркнуть, при этом ранг матрицы не изменится. Ранг расширенной матрицы равен трем, так как она имеет не равный нулю минор третьего порядка, например, минор, составленный из первого, второго и последнего столбцов расширенной матрицы
Система линейных алгебраических уравнений
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
 | (1) |
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Содержание
Матричная форма
Система линейных уравнений может быть представлена в матричной форме как:

Здесь 



Эквивалентные системы линейных уравнений
Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.
Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.
Система линейных алгебраических уравнений

где 
В частности, если сама матрица 


Методы решения
Прямые (или точные) методы позволяют найти решение за определённое количество шагов. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.
Прямые методы
Итерационные методы
Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения

эквивалентного начальной системе линейных алгебраических уравнений. При итерации 

Среди итерационных методов можно отметить самые популярные:
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Система линейных алгебраических уравнений» в других словарях:
Прямоугольная система линейных алгебраических уравнений — Определение Для системы из уравнений с неизвестными ( ) любые переменных называются базисными, если определитель составленный из коэффициентов при этих неизвестных отличен от нуля (остальные переменных называются свободными). Базисным решением… … Википедия
Решение систем линейных алгебраических уравнений — Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений. Содержание 1 Однородные системы 1.1 Пример … Википедия
Система линейных уравнений — Системы линейных уравнений: Система линейных алгебраических уравнений Система линейных дифференциальных уравнений … Википедия
Система уравнений — У этого термина существуют и другие значения, см. Система (значения). Система уравнений это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных. Формальная запись общего вида… … Википедия
Система компьютерной алгебры — Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Добавить иллюстрации. Викифицировать список литературы, используя … Википедия
Квадратная система уравнений — Системы линейных уравнений: Система линейных алгебраических уравнений Система линейных дифференциальных уравнений … Википедия
Определенная система уравнений — Системы линейных уравнений: Система линейных алгебраических уравнений Система линейных дифференциальных уравнений … Википедия
Линейная система — Не следует путать с Система линейных алгебраических уравнений. Линейная система математическая модель системы, оператор которой обладает свойством линейности. Необходимые условия линейности Гомогенность – при изменении амплитуды входного сигнала… … Википедия
Нормальная форма дифференциальных уравнений — есть наипростейшая эквивалентная форма исходных уравнений. Нормальная форма получается с помощью специальных замен зависимых и независимых переменных задачи с целью максимального упрощения структуры уравнений. В математике эти замены переменных… … Википедия
Численное решение системы нелинейных уравнений — Содержание 1 Постановка задачи 2 Численные методы решения уравнений 2.1 Метод простой итерации … Википедия