Что такое след в геометрии
Урок геометрии по теме: «Построение сечений в многогранниках методом следов». 10-й класс
Разделы: Математика
Класс: 10
Девиз: “Мы одна семья, мы учимся все вместе”
Обучающая цель: формирование умений и навыков построения сечений методом следов.
Воспитывающая цель: воспитывать чувство сплоченности, взаимопомощи, воспитывать умения работать индивидуально над задачей.
Тип урока: урок формирования и совершенствования знаний.
Формы организации учебной деятельности: групповая, индивидуальная, коллективная.
Техническое обеспечение урока: мультимедийный проектор, набор геометрических тел (куб, параллелепипед, пирамида).
Организационный момент: Рассаживаемся на 3 группы по 5 человек. На каждом столе – набор тел, памятки-опоры, карточки для индивидуальной работы по построению сечений.
Слово учителя: Вы изучили аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых и плоскостей в пространстве. При решении многих стереометрических задач используют сечение многогранника плоскостью. Существует несколько методов построения сечений многогранника плоскостью: метод следов, метод внутреннего проектирования и комбинированный метод.
Мы изучим метод следов.
1) Ребята, я предлагаю вам повторить и вспомнить некоторые геометрические понятия и определения.
2) Ребята, перед вами пример неправильного построения сечения куба АС1 плоскостью, проходящей через заданные точки N, C, D1.
А рядом сечение построено верно.
На уроках черчения вы пользовались определением: Сечение – это изображение фигуры, которая получается при мысленном рассечении тела плоскостью.
Вот таким определением мы и будем пользоваться сегодня на уроке.
В тетраэдре сечениями могут быть только треугольники или четырехугольники, а в параллелепипеде – треугольники, четырехугольники, пятиугольники или шестиугольники.
Рассмотрим пример (мультимедийный проектор).
Построить сечение куба, проходящее через точки М, N, L.
Алгоритм построения
Следы плоскости
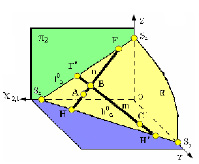
На рисунке показана плоскость общего положения α. Она пересекает плоскости проекций П1, П2, П3 по прямым h0α, f0α и p0α. Эти прямые называются горизонтальным, фронтальным и профильным следом плоскости α.
Оси координат пл. α пересекает в точках Xα, Yα и Zα. Они называются точками схода следов. При этом Xα = h0α ∩ f0α, Yα = h0α ∩ p0α, Zα = f0α ∩ p0α. Здесь знак ∩ означает пересечение.
На комплексном чертеже плоскость можно задать проекциями двух её следов. Это обеспечивает наглядность изображения и удобство при выполнении ряда построений. Стоит отметить, что угол, образованный следами плоскости на комплексном чертеже, не равен углу между ними в пространстве.
Алгоритм построения следов плоскости
На рисунке, который представлен ниже, некоторая плоскость α задана проекциями двух пересекающихся прямых a и b. Чтобы найти её следы, необходимо:
Решение задачи можно сократить. Для этого, построив горизонтальный след плоскости, фронтальный нужно провести через Xα и одну из точек, Fa или Fb. Таким образом, вместо четырех следов прямых a и b будет достаточно найти три.
Презентация по геометрии на тему «Метод следов»
Описание презентации по отдельным слайдам:
Построение сечений: метод следов Астрахань – 2012 г.
Существует три основных метода построения сечений многогранников: Метод следов. Метод вспомогательных сечений. Комбинированный метод.
Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.
Задача 1. Дана призма ABCDA1B1C1D1. Построить сечение призмы плоскостью, проходящей через точки P, Q, R. P Q R
Задача 1. Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
Задача 1. Прямая PQ, которая принадлежит сечению, пересекается с прямой АВ в точке S1.
Задача 1. Аналогично получаем точку S2 пересечением прямых QR и BC.
Задача 1. Прямая S1S2 пересекает сторону AD в точке U, сторону CD в точке Т. Аналогично получаем TU и RT. Соединим точки P и U, так как они лежат в одной плоскости грани АА1D1D.
Задача 1. PQRTU – искомое сечение.
Задача 2. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки M, N, P.
Задача 2. Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
Задача 2. Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.
Задача 2. Так как точка M также принадлежит плоскости сечения и пересекает прямую АА1 в некоторой точке Х.
Задача 2. Точки X и N лежат в одной плоскости грани АА1D1D, соединим их и получим прямую XN.
Задача 2. Эта прямая пересечет сторону В1С1 в точке Y. Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A1B1C1D1, параллельную прямой NP.
Задача 2. Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.
Задача 3. На ребрах АА’ и В’С’ призмы АВСА’В’С’ зададим соответственно точку P и Q. Построим сечение призмы плоскостью (PQR), точку R которой зададим в грани ВСВ’С’.
Задача 3. Так как точки Q и R лежат в плоскости (ВСС’), то в этой плоскости лежит прямая QR. Проведем ее. Это след плоскости (PQR) на плоскость(ВСС’).
Задача 3. Так как точки Р и С лежат в плоскости (АСС’), то прямая РС» лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АСС’).
Задача 3. Находим точку V, в которой прямая РС» пересекает ребро А’С’. Это след плоскости (PQR) на ребре А’С’.
Задача 4. На ребрах АА’ и В’С’ призмы АВСА’В’С’ зададим соответственно точку P и Q. Построим сечение призмы плоскостью (PQR), точку R которой зададим в грани А’В’С‘.
Задача 4. Так как точки Q и R лежат в плоскости (А’В’С’), то в этой плоскости лежит прямая QR. Проведем ее. Это след плоскости (PQR) на плоскости (А’В’С’).
Задача 4. Так как точки Р и Е’ лежат в плоскости (АСС’), то в этой плоскости лежит прямая РЕ’. Проведем ее. Это след плоскости (PQR) на плоскости (АСС’).
Спасибо за внимание!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-405648
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Большинство родителей в России удовлетворены качеством образования в детсадах
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Российские юниоры завоевали 6 медалей на Международной научной олимпиаде
Время чтения: 2 минуты
Путин призвал повышать уровень общей подготовки в колледжах
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Научная электронная библиотека
Пиралова О. Ф., Ведякин Ф Ф.,
2.7. Следы плоскости
Следом плоскости α называется линия пересечения этой плоскости с плоскостью проекций.
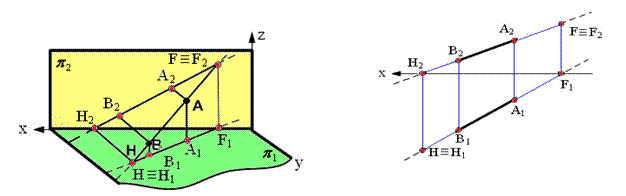
На рис. 2.19. изображена плоскость общего положения α(m∩n), образованная двумя пересекающимися прямыми, проходящими через точки А и В, расположенными в первом октанте.
Для построения следов плоскости на комплексном чертеже, необходимо помнить, что след плоскости – это линия, значит необходимо найти две точки, через которые пройдет эта линия, т. е. след плоскости. При построении плоскости за такие точки можно принять следы любых прямых линий, принадлежащих этой плоскости.
На рис. 2.19 в горизонтальной плоскости проекций π1 её горизонтальный след h0α проходит через горизонтальные следы Н и Н’ прямых m и n, а во фронтальной плоскости проекций π2 – фронтальный след плоскости f0α проходит через фронтальные следы прямых F и F’.
Рис. 2.19. Пример изображения следов плоскости α в пространстве
Для нахождения следов плоскости нужно применить правило построения следов прямых линий, который был рассмотрен выше (§2.4). Для построения горизонтального следа плоскости необходимо построить два горизонтальных следа прямых, принадлежащих плоскости, а для построения фронтального следа плоскости – два горизонтальных следа прямых, принадлежащих плоскости α(m∩n).
В системе двух плоскостей проекций π1 и π2 плоскость в общем случае имеет два следа: горизонтальный ha0 и фронтальный fa0, которые являются пересечением плоскости α соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.19, 2.20).
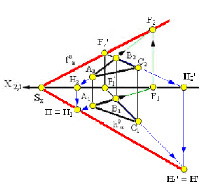
Рис. 2.20. Пример изображения следов плоскости и их алгоритм построения на комплексном чертеже
Точки пересечения плоскости α с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно Sx, Sy, Sz (рис. 2.16). На рис. 2.20. приведен комплексный чертеж плоскости треугольника АВС и разобран пример построения двух следов этой плоскости – горизонтального ha0 и фронтального fa0. Для этого выполнено построение горизонтальных следов прямых АВ и ВС, принадлежащих плоскости треугольника. Эти следы обозначены буквами Н и Н’. Решение на рисунке выполнено синими линиями со стрелками. Аналогичное построение выполнено и для фронтального следа линиями зелёного цвета. Порядок построения следов ясен из рисунка.
Вопросы для самоконтроля
1. Когда точка принадлежит какой либо плоскости проекций?
2. Как может быть задана прямая на комплексном чертеже?
3. Какие основные свойства прямой общего положения?
4. Какие частные положения относительно плоскостей проекций может занимать прямая линия?
5. Когда прямая линия может принадлежать плоскости проекций?
6. Какие прямые являются проецирующими?
7. Что называется следом прямой?
8. Как определяются на комплексном чертеже следы прямой линии?
9. Как на комплексном чертеже может быть задана плоскость?
10. Какие плоскости являются проецирующими?
11. Какие плоскости являются плоскостями уровня?
12. Какие плоскости являются плоскостями частного положения?
13. Что называется следом плоскости и как он определяется?
[1] То́чка – абстрактный объект в пространстве, не имеющий никаких измеримых характеристик (нульмерный объект).
Научная электронная библиотека
2.4. Следы прямой линии
Следом прямой линии называется точка пересечения прямой с плоскостью проекций.
В системе двух плоскостей проекций p1 и p2 прямая в общем случае имеет два следа:
Это точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций (рис. 2.11, а).
Установим правило нахождения следов прямой.
Для нахождения горизонтального следа прямой необходимо:
1) продолжить фронтальную проекцию прямой а до пересечения с осью Х (получим точку НХ º Н2)
2) восстановить перпендикуляр в точке НХ к оси Х (провести линию связи перпендикулярную к оси Х);
3) продолжить горизонтальную проекцию прямой а до пересечения с перпендикуляром;
4) полученная точка пересечения и будет горизонтальным следом прямой а Н º Н1 (рис. 2.11, б).
Рис. 2.8. Прямая, перпендикулярная Рис. 2.9. Прямая, перпендикулярная
горизонтальной плоскости проекций фронтальной плоскости проекций
Рис. 2.10. Прямая, перпендикулярная профильной плоскости проекций
Рис. 2.11. Изображение следов прямой линии:
Для нахождения фронтального следа прямой необходимо:
1) продолжить горизонтальную проекцию прямой а до пересечения с осью Х (точка FXº F1);
2) восстановить перпендикуляр в точке FX к оси Х;
3) продолжить фронтальную проекцию прямой до пересечения с перпендикуляром;
4) полученная точка пересечения Fº F2 будет фронтальным следом прямой а (рис. 2.11, б).
В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическими фигурами будут только те, которые расположены в первом октанте.
Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.