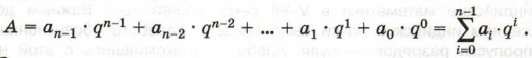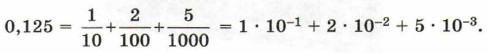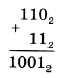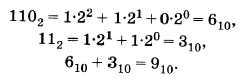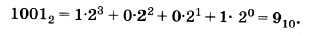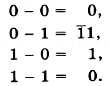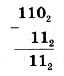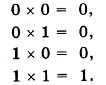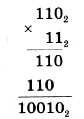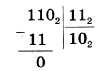Позиционные системы счисления

Существует бесконечно много позиционных систем счисления. Каждая из них определяется целым числом q > 1, называемым основанием системы счисления. Основание определяет (даёт) название системы счисления: двоичная, троичная, восьмеричная, шестнадцатеричная, q-ичная и т. д. Можно говорить «система счисления с основанием q» (табл. 3.1).

В q-ичной системе счисления q единиц какого-либо разряда образуют единицу следующего разряда.

Целое число без знака А в q-ичной системе счисления представляется в виде конечной суммы степеней числа q — суммы разрядных слагаемых:

Последовательность чисел, каждое из которых задаёт «вес» соответствующего разряда, называется базисом позиционной системы счисления.

Свёрнутой формой записи числа мы пользуемся в повседневной жизни, иначе её называют естественной формой или цифровой.

Развёрнутая форма записи чисел также всем хорошо известна. Ещё в начальной школе дети учатся записывать числа в виде суммы разрядных слагаемых. Например:

125 248 = 1 • 100 000 + 2 • 10 000 + 5 • 1 000 + 2 • 100 + 4 • 10 + 8 • 1.

Если представить разряды в виде степей основания, то получим:

Аналогичным образом представляются и дроби:

Иногда бывает полезно преобразовать развёрнутую форму записи числа так, чтобы избежать возведения основания системы счисления в степени.

Например, можно записать:

125 248 = 1 • 10 5 + 2 • 10 4 + 5 • 10 3 + 2 • 10 2 + 4 • 10 1 + 8 • 10 0 =
= ((((1 • 10 + 2) • 10 + 5) • 10 + 2) • 10 + 4) • 10 + 8;

Такую форму представления числа называют разложением по схеме Горнера.

Изучая десятичную систему счисления с раннего возраста и используя её в повседневной практике, многие люди не догадываются о существовании других систем счисления.

Но так ли хороша десятичная система счисления? Великий французский математик и естествоиспытатель Блез Паскаль (1623-1662) писал: «Десятичная система построена довольно неразумно, конечно, в соответствии с людскими обычаями, а вовсе не с требованиями естественной необходимости, как склонно думать большинство людей». В ряде теоретических и практических задач некоторые системы счисления, отличные от десятичной, имеют определённые преимущества.

Первые механические счётные машины были разработаны на основе десятичной системы счисления. Для реализации десяти устойчивых состояний в них использовались сложные системы зубчатых колёс (рис. 3.1). Такие машины были очень громоздки, занимали много места.

Так, если бы проект Аналитической машины Ч. Беббиджа — механического прототипа появившихся спустя столетие ЭВМ — был реализован, то по размерам такая машина сравнялась бы с локомотивом. В 1937 году немецкий инженер К. Цузе создал вычислительную машину, основанную на принципах действия аналитической машины Ч. Беббиджа. Она была механической, но работала на основе двоичной системы счисления, что позволило значительно уменьшить её размеры: машина занимала всего 2 м 2 на столе в квартире изобретателя!

В наши дни большой практический интерес представляют двоичная, троичная, восьмеричная и шестнадцатеричная системы счисления.

Источник

Что такое свернутая запись числа

Позиционные системы счисления

Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от ее положения в записи числа.
Основание — основная характеристика позиционной системы счисления равно количеству цифр, составляющих ее алфавит. Им может служить любое натуральное число q > 1. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения цифр в соседних разрядах числа различаются в количество раз, равное основанию системы.

Десятичная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой производим все наши вычисления, — пример позиционной системы счисления. В ней алгоритмические числа образуются следующим образом: значения цифр умножаются на «веса» соответствующих разрядов и все полученные значения складываются. Это отчетливо прослеживается в числительных русского языка, например: «три-ста пять-десят семь».

Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.

В позиционной системе счисления с основанием q любое число может быть представлено в виде:

Запись числа по этой формуле называется развёрнутой формой записи.

Здесь:
А — число;
q — основание системы счисления;
a_i — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
q i — «вес» i-ro разряда.

Свёрнутой формой записи числа называется его представление в виде:

Пример 1. Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:

Источник

Урок 19
Развернутая и свернутая формы записи чисел. Перевод из произвольной в десятичную систему счисления

§ 4.1. Кодирование числовой информации

Содержание урока

4.1.2. Арифметические операции в позиционных системах счисления

4.1.2. Арифметические операции в позиционных системах счисления

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным вам правилам.

Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:

0 + 0 = 0,
0 + 1 = 1,
1 + 0 = 1,
1 + 1 = 10.

Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда значение цифры в нем становится равным или большим основания системы счисления. Для двоичной системы счисления это значение равно двум.

Сложение многоразрядных двоичных чисел производится в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа 110₂ и 11₂:

Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим:

Теперь переведем результат двоичного сложения в десятичное число:

Сравним результаты — сложение выполнено правильно.

Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел.

При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой:

Вычитание многоразрядных двоичных чисел производится в соответствии с вышеприведенной таблицей вычитания с учетом возможных заемов из старших разрядов. В качестве примера произведем вычитание двоичных чисел 110₂ и 11₂:

Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел:

Умножение многоразрядных двоичных чисел производится в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя. В качестве примера произведем умножение двоичных чисел 110₂ и 11₂:

Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 110₂ на 11₂:

Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему.

Задания для самостоятельного выполнения

4.6. Задание с развернутым ответом. Выполните сложение, вычитание, умножение и деление двоичных чисел 1010₂ и 10₂

Cкачать материалы урока

Источник

Презентация по «Информатике и ИКТ» Развернутая и свернутая формы записи чисел. Перевод из произвольной в десятичную систему счисления

Описание презентации по отдельным слайдам:

Урок по информатике и ИКТ 8 класс. Тема урока: Презентацию подготовил учитель «Информатики и ИКТ» ГБОУ Школы № 1905 Панин Геннадий Геннадьевич

Содержание 1. Основные понятия. Виды систем счисления 2. Непозиционные системы счисления 3. Позиционные системы счисления 4. Десятичная система счисления 5. Двоичная система счисления 6. Восьмеричная система счисления 7. Шестнадцатеричная система счисления 8. Перевод чисел в десятичную сс 9. Задания для самостоятельного выполнения

зависит не зависит

Непозиционные системы счисления

CDLVII =457 X I I = 12 Найдите значения чисел:

– основание (p) Совокупность всех цифр – алфавит Позиционные системы могут иметь различный алфавит (2,3,4 знака). Позиционные системы счисления Каждая позиционная система счисления имеет определенный алфавит и основание. системы счисления

Алфавиты систем счисления Для записи чисел в позиционной системе с основанием р нужно иметь алфавит из р цифр. При р > 10 к десяти арабским цифрам добавляют латинские буквы. Позиция цифры в числе называется разрядом. Основание Название Алфавит р = 2 Двоичная 0 1 р = 3 Троичная 0 1 2 р = 8 Восьмеричная 0 1 2 3 4 5 6 7 р = 16 Шестнадцатеричная 0 1 2 3 4 5 6 7 8 9 A B C D E F

ПРИМЕРЫ: (перепиши, вставляя пропущенные числа) p = 10 (десятичная с/c) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 и т.д. p = 4 (четверичная с/c) 1 2 3 10 11 12 13 20 21 22 23 30 __ __ __ __ 3. p = 2 (двоичная с/c) 1 10 11 100 101 110 111 1000 ___ 1010 1011 ____ ___ ___ ___ 10000 _____ _____ 4. p = 16 (шестнадцатеричная с/c) 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B ___ ___ ___ ___ 31 32 33 100 1001 1C 1D 1E 1F

Рассмотрим десятичное число 555: 5 5 5 10 единицы десятки сотни Из двух написанных рядом одинаковых цифр левая в десять раз больше правой.

Двоичная система счисления является позиционной системой счисления. Алфавит двоичной системы – две цифры (0,1), основание равно 2. Из двух написанных рядом одинаковых цифр левая в два раза больше правой.

Восьмеричная система счисления является позиционной системой счисления. Алфавит восьмеричной системы – цифры (0,1,2,3,4,5,6,7), основание равно 8. Из двух написанных рядом одинаковых цифр левая в восемь раз больше правой.

Шестнадцатеричная система счисления является позиционной системой счисления. Алфавит шестнадцатеричной системы – цифры (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F), основание равно 16. Из двух написанных рядом одинаковых цифр левая в шестнадцать раз больше правой. (Десятичное значение: A=10, B=11, C=12, D=13, E=14, F=15)

Задания для самостоятельного выполнения Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6

Ответ: а) 341 (р=5) в) 222 (р=3) б) 123 (р=4) г) 111 (р=2) Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: а) 341 б) 123 в) 222 г) 111

Ответ: 11112 = 1510. Какое максимальное число можно записать в двоичной системе счисления четырьмя цифрами? Переведите полученное число в десятичную систему счисления.

Ответ: четное число в двоичной системе счисления оканчивается на 0, а нечетное – на 1. а) 1012 = 510 б) 1102 = 610 в) 10012 = 910 г) 1002 = 410 Определите четное число или нечетное: а) 1012 б) 1102 в) 10012 г) 1002 Сформулируйте критерий четности в двоичной системе счисления.

Ответ: да, если считать числа в задаче, представленными в двоичной системе счисления: 112= 121 + 120 = 310; 1102 = 122 + 121 + 020 = 4 + 2 = 610 Было 11 яблок. После того как каждое яблоко разрезали пополам, стало 110 половинок. Возможно ли это? Обоснуйте ответ.

Ответ: алфавит пятеричной системы счисления – цифры (0,1,2,3,4). 325 = 351 + 250 = 15 + 2 = 1710 Выпишите алфавит традиционной позиционной пятеричной системы счисления. Переведите число 325 в десятичную систему счисления.

Домашнее задание: 1) § 4.1.1 стр.104 2) выполнить «задания для самостоятельного выполнения» № 4.1, 4.4 на стр.108 Урок окончен

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

Курс профессиональной переподготовки

Информатика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-403149

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Рособрнадзор объявил сроки и формат ЕГЭ

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Информатика

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Развиваясь, древний человек стал испытывать потребность в способах выражения количества. Подсчет убитых животных, количество врагов или соседей – причин становилось все больше. Сначала люди использовали только понятия «один», «много». После стали использовать понятие «пара», чтобы обозначить два предмета, это намного облегчило жизнь.

Постепенно перешли к использованию подручных средств – пальцев на руках и ногах, зарубок на коре дерева, кости животного или узелков на канате. Именно такие примитивные «счетные машины» позволили через тысячи лет узнать, что предки умели не просто считать, но даже умудрялись фиксировать результаты подсчета.

Кроме зарубок и узелков появилась потребность в символах, выражающих большее количество чего-либо, чем «один». Тогда были придуманы первые знаки для выражения больших значений. Так, египтяне, использовали знаки для цифр 1, 5, 10. Число 324 в их системе выглядело так:

А описание чисел при помощи специальных знаков и является системой счисления.

Системы счисления – виды, особенности

Система счисления (СС) – способ выражения чисел при помощи специальных правил и знаков, которые называются цифрами.

Все существующие системы делят на 2 группы:

Чтобы выразить число 475, достаточно по порядку написать 3 символа, 475, выражая 5 единиц, 7 десятков и 4 сотни.

К этой группе также относятся СС с различными основаниями (2,8,16).

Еще одна особенность – чтобы выразить число и не использовать сотни символов, применяется прибавление и вычитание. Написать 475 римскими знаками можно так CCCCXXXXXXXIIIII, но это нерационально. Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.

Правильным считается тот вариант, при котором получается меньше символов.

Интересно. Первой позиционной СС была вавилонская и была она шестнадцатиричная! А в 19 веке использовали двенадцатеричную СС.

Алфавит СС – знаки, которые используются для обозначения цифр.

Основание – количество знаков, которыми кодируются числа. Еще оно показывает отличие между цифрами на разных позициях. Основание – целое число, начиная с 2.

Важно. Если в тексте идет речь о различных системах, то чтобы уточнить, какая используется основа, ставится подстрочный знак: 1254₈, 01100111₂. Примеры? Если же обозначения нет, по умолчанию это десятичная (12549).

Разряд – положение, позиция обозначения цифры в числе. Пример?

Непозиционные СС, их особенности

Первоначально древние люди ставили отметки (черточки-зарубки, точки), чтобы обозначить количество того или иного предмета. Отклики этого подхода все еще встречаются (полоски у военных, счетные палочки).

Постепенно от единиц они переходили к группам предметов по 3, 5, 10 единиц. Постепенно такие группы стали обозначаться определенными символами, что позволило сократить размер записи.

Римская СС

В ней определенным цифрам отвечают латинские буквы. Их сумма и будет числом.

Основные рекомендации при пользовании римскими цифрами:

Таблица римских цифр

Недостаток этой СС в том, что для больших чисел недоступны операции сложения или другие, ещё она сложная и громоздкая. Зато римские цифры отлично вписались там, где нужна нумерация и эстетика: циферблаты, номера глав, списки, серии документов.

Основные позиционные СС, правила перевода

Двоичная система счисления

Систему, на которой основывается работа компьютеров, придумал гениальный немецкий ученый Г.В. Лейбниц (еще до 19 века!). Он придумал и описал СС, в которой все вычисления проводятся при помощи двух простейших символов – 0 и 1.

Компьютер, как механическое устройство, получает команды в виде двоичной кодировки. Он не в силах понять сложные задания, человеческую речь, музыку или тысячи оттенков, а переводя/кодируя всю необходимую информацию при помощи 0 и 1 (сеть, отсутствие сети), можно передать ему любые команды или информацию. Естественно, такие задания выглядят как огромные массивы двух знаков.

Алгоритм перевода чисел из десятичной в двоичную систему:

Этот порядок действия позволят переводить в любую позиционную СС. В данном случае, основа – 2, остаток 2 +7*10 1 +9*10 0 = 579₁₀.

Обычно мы пользуемся свернутой формой записи чисел, то есть без разбивки на разряды и умножения на основу.

А чтобы было легче, пользуются готовой таблицей степеней 2.

Альтернативный способ преобразования для гуманитариев

Для начала нужно написать степени двойки, начиная с самой большой:

Далее нужно отнимать от числа максимальную степень двойки и напротив нее ставить 1, если есть в исходном варианте или 0, если его нет.
Перевод числа 579

Если же оно на 1 больше, то число будет начинаться и заканчиваться на 1, а внутри – сплошные 0.

Основой такой системы является 8, а числа восьмеричной системы 0-7. Данная система счисления является позиционной и целочисленной. Применяется в сферах, связанных с цифровыми технологиями, особенно в Linux-программном обеспечении (права доступа, исполнения).

Пример: Перевести 579₈ из десятичной в восьмеричную систему счисления:

Обратный перевод из восьмеричной СС в десятичную:

1103₈ = 1∙8 3 +1∙8 2 +0∙8 1 +3∙8 0 = 512+64+0+3 = 579₁₀

Альтернативный вариант таблицы степеней

Шестнадцатеричная СС

Это целочисленная система с основанием 16 (символы шестнадцатеричной системы счисления 0-9 и буквы A – F). Используется в реализации компьютерного программирования и документации на низком уровне, так как 8-битный байт, для записи которого удобно использовать 2 цифры из шестнадцатеричной системы.

Стандарт Юникод использует 4 и более символов 16-ой СС.

Для записи цвета из красного, зеленого и синего (R, G и B) также используют эту систему.

Алгоритм преобразования чисел в 16СС

Способ преобразования аналогичный предыдущим – расписывание числа как многочлена с учетом степеней 16. Для этого число делится на 16, в итоге – перечень остатков от деления, записанных наоборот.

В сети есть калькуляторы, способные выполнять преобразование чисел в различные СС и обратно (некоторые даже с детальным описанием процесса).

Арифметика для 2СС

Принципы выполнения простейших арифметических операций одинаковы для любых позиционных систем, независимо от основы:

Особенности арифметики СС с разными основами:

Примеры арифметических операций:

Для удобства разработаны готовые таблицы сложения в различных системах:

Сложение в 8-ой СС в 16СС

С их помощью можно быстро суммировать в различных СС.

Сложение для разных СС на примере 15 и 6:

Если необходимо сложить числа из разных систем, их приводят к одной основе. Самым простым вариантом будет перевод в десятичную систему, решение простого примера и перевод результата в любую из систем.

Рассмотрим сумму 43₈ и 56₁₆. Результат можно выразить в любой СС, но проще привести к 8- или 16-ричной:

Переводим число 56 в восьмеричную через двоичную:

Умножение в 8-ой СС

Сравнение систем

СС могут быть с произвольной основой, но популярны 2,8,10,16-ые.

Сравнительная таблица разных систем счисления:

Перевод числа 75 в разные системы:

Правила перевода из двоичной, восьмеричной и шестнадцатеричной в 10СС:

Исходный вариант следует разделить на тройки цифр, с крайней справа. Если не хватает, старший разряд дополнить 0. Далее под каждой триадой ставится подходящий символ из 8‑ой системы.

Рассмотрим перевод на примере числа 579, которое соответствует 1001000011₂

Правила перевода из двоичной в шестнадцатеричную систему счисления:

Число разбивается по 4 знака, начиная справа (с меньшего разряда). Если не будет хватать символов у старшего разряда, тетраду дополняют нулями.

Сравнительный перевод дробей в СС

Чтобы перевести правильные дроби из 10-ой СС в другие позиционные, следует придерживаться правила, которое хорошо видно на примере перевода числа 0,35:

Удобно писать над каждой цифрой порядок, а дальше ее умножить на основу СС в степени разряда.

Перевод целых и дробей в 2СС, 8СС, 16СС:

Таблицы истинности

При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.

Основные логические операции

Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.

Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:

Фрагмент таблицы истинности для конъюнкции.

Так выражаются условия для всех логических операций.

Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.

Источник