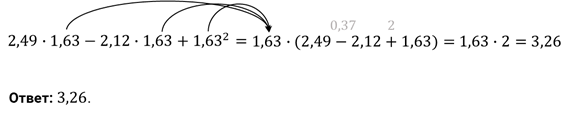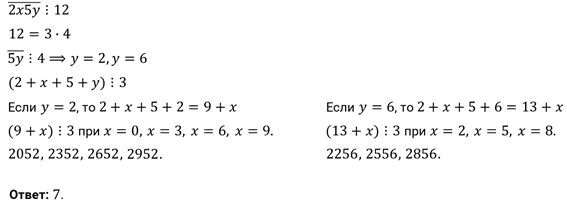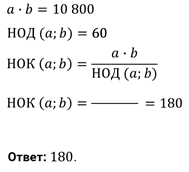Что такое свойства числа
Числа: натуральные, целые, рациональные, иррациональные, действительные
Натуральные числа
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
сочетательное свойство сложения
переместительное свойство умножения
сочетательное свойство умножения
распределительное свойство умножения
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
Подробнее об иррациональных числах в разделе Иррациональные числа.
Действительные числа
Действительные числа – это все рациональные и все иррациональные числа.
Множество действительных чисел обозначается латинской буквой R.
Числа и их свойства
Урок 1. Подготовка к ЕГЭ по математике
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Числа и их свойства»
Напомним, что понятие «натуральное число» является первоначальным, неопределяемым. Оно возникло из потребностей счёта. Множество натуральных чисел обозначают 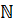
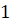
Число, например, состоящее из а сотен, b десятков и c единиц, записывается в виде:
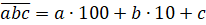
В следующей записи 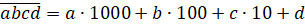
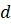
Вы уже знаете, что натуральные числа можно сравнивать между собой, складывать и умножать. Из большего натурального числа можно вычесть меньшее.
Если натуральное число 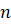
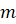
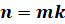

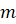
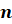
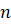
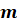
Вот такая запись 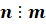
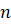
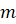
Натуральное число, не равное единице, называется простым, если оно имеет только два делителя: единицу и само это число.
Например: 2, 3, 5, 7, 11, 17 — простые числа.
Натуральное число называется составным, если оно имеет более двух делителей. Например: 6, 15, 24, 36 — составные числа.
Число 1 не является ни простым, ни составным. Простых чисел бесконечно много. Каждое составное число разлагается на простые множители и притом единственным образом.
Сформулируем признаки делимости натуральных чисел:
1. Для делимости на 2 нужно, чтобы последняя цифра числа была чётная или 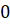
2. Для делимости на 3 нужно, чтобы сумма цифр числа делилась на 3.
3. Для делимости на 4 нужно, чтобы две последние цифры числа были 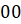
4. Для делимости на 5 нужно, чтобы последняя цифра числа была 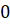
5. Для делимости на 8 нужно, чтобы три последние цифры числа были 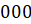
6. Для делимости на 9 нужно, чтобы сумма цифр числа делилась на 9.
7. Для делимости на 10 нужно, чтобы последняя цифра числа была 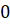
8. Для делимости на 11 нужно, чтобы разность между суммой цифр, стоящих на чётных местах, и суммой цифр, стоящих на нечётных местах, делилась на 11.
9. Для делимости на 25 нужно, чтобы две последние цифры числа были 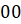
Наибольшее из натуральных чисел, на которое делятся числа 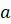
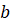
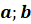
Числа 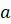
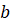
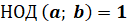
Наименьшее из натуральных чисел, которое делится на числа 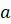
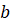
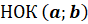
Разделить натуральное число 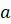
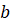
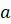
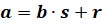
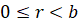
Например, 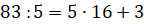
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Найдите значение выражения 
Задание второе. Найдите наибольшее натуральное число, которое при делении на 15 с остатком даёт частное, равное 19.
Задание третье. Найдите все натуральные числа вида 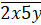
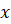
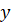
Задание четвёртое. Произведение двух чисел равно 10 800, а их НОД равен 60. Найдите НОК этих чисел.
Задание пятое. Найдите все пары натуральных чисел, НОД которых равен 5, а НОК равно 105.
Задание шестое. Сумма цифр искомого двузначного числа равна 8. Если цифры этого числа переставить, то получится число, которое меньше искомого на 18. Как велико искомое число?
Задание седьмое. В двузначном числе цифра десятков на 4 больше цифры единиц. Когда это число разделили на цифру единиц, то в частном получилось 24, а в остатке число, которое на 2 меньше делителя. Найдите заданное число.
Задание восьмое. В комнате стоят табуретки и стулья. У каждой табуретки по 3 ноги, у каждого стула по 4 ноги. Когда на всех табуретках и стульях сидят люди, то в комнате всего 39 ног. Сколько стульев и сколько табуреток в комнате?
Задание девятое. Когда брату было столько лет, сколько сестре сейчас, им вместе было 15 лет; когда сестре будет столько лет, сколько сейчас брату, им вместе будет 27 лет. Найдите возрасты брата и сестры.
Свойства чисел
Ниже приведены характеристики чисел с примерами, которые рассматривает сайт aboutnumber.ru
Сумма цифр
Сумма цифр, из которых состоит число.
Произведение цифр
Произведение цифр, из которых состоит число.
Количество цифр в числе
Отображение количества цифр в числе (если их больше 4-х). Это удобно, так как не всегда можно на глаз определить порядок числа.
Все делители числа
Полный список делителей, на которые делится число без остатка.
Наибольший делитель из ряда степеней двойки
Ряд степеней двойки — это ряд вида 1, 2, 4, 8, 16, 32, 64, 128, 256 и т.д. Эти числа являются основными числами в бинарной математике (в двоичной записи), так как ими можно охарактеризовать объем информации.
Количество делителей
Суммарное число делителей.
3638143886 → всего 32 делителя
Сумма делителей
Сумма всех делителей числа.
77432243032 → сумма делителей 145185455700
Простое число
Проверка на простое число. Простое число — это число, которое делится без остатка только на единицу и само себя. Таким образом у простого числа может быть всего два делителя.
Полупростое число
Проверка на полупростое число. Полупростое число — число, которое можно представить в виде произведения двух простых чисел. У полупростого числа два делителя — оба простые числа.
Обратное число
Два числа называются обратными если их произведение равно единице. Таким образом обратным к заданному числу N всегда будет 1/N.
Проверка: 0.008 * 125 = 1
Факторизация
Факторизация числа — представление числа в виде произведения простых чисел.
Двоичный вид
Двоичное, оно же бинарное представление числа. Это запись числа в системе счисления с основанием два.
Троичный вид
Троичное представление числа. Это запись числа в системе счисления с основанием три.
Восьмеричный вид
Восьмеричное представление числа. Это запись числа в системе счисления с основанием восемь.
Шестнадцатеричный вид (HEX)
Шестнадцатеричное представление числа. Часто его пишут английскими буквами «HEX». Это запись числа в системе счисления с основанием шестнадцать.
Перевод из байтов
Конвертация из байтов в килобайты, мегабайты, гигабайты и терабайты.
29141537 (байт) → 27 мегабайтов 810 килобайтов 545 байтов
В случаем, если число меньше чем 16777216, то его можно представить в виде цвета. Шестнадцать миллионов цветов, которые можно закодировать стандартной цветовой схемой компьютера.
RGB(126, 141, 204) или #7E8DCC
Наибольшая цифра в числе (возможное основание)
Наибольшая цифра, встречающаяся в числе. В скобках указана система счисления, с помощью которой, возможно, записано это число.
347524172 → 7 (8, восьмеричный вид)
Перевод двоичной/троичной/восьмеричной записи в десятичную
Число, записанное с помощью единиц и нолей — имеет бинарный вид, таким образом его можно перевести в десятичную систему счисления.
Число, записанное с помощью единиц, нолей и двоек — имеет троичный вид.
Если с помощью цифр до семи (включая) — восьмеричный вид числа.
Число Фибоначчи
Проверка на число Фибоначчи. Числа Фибоначчи — это последовательно чисел, в которых каждый последующий элемент равен сумме двух предыдущих.
Ряд Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.
Позиция в ряду Фиббоначчи
Характеризует порядковый номер числа в ряду Фибоначчи.
21 → 8-е число в ряду Фибоначчи
Нумерологическое значение
Нумерологическое значение вычисляется путем последовательного сложения всех цифр числа до тех пор, пока не не получится цифра от 0 до 9. В нумерологии каждой цифре соответствует свой характер.
8372890 → 8 + 3 + 7 + 2 + 8 + 9 + 0 = 37 → 3 + 7 = 10 → 1 + 0 = 1
мужество, логика, независимость, самостоятельность, индивидуализм, смелость, решительность, изобретательность
Синус числа
Расчет тригонометрической функции синуса числа в радианах.
Косинус числа
Расчет тригонометрической функции косинуса числа в радианах.
Тангенс числа
Расчет тригонометрической функции тангенса числа в радианах. Чтобы получить котангенс числа, надо единицу поделить на величину тангенса.
Натуральный логарифм
Это логарифм числа по основанию константы e ≅ 2,718281828459.
Десятичный логарифм
Это логарифм числа по основания десять.
Квадратный корень
Квадратный корень из введенного числа.
Кубический корень
Кубический корень из введенного числа.
Квадрат числа
Число, возведенное в квадрат, то есть умноженное само на себя.
Перевод из секунд
Конвертация числа секунд в дни, часы, минуты и секунды.
1805506 (секунд) → 2 недели 6 дней 21 час 31 минута 46 секунд
Дата по UNIX-времени
UNIX-время или UNIX-дата — количество секунд, прошедших с полуночи 1 января 1970 года (по UTC). Таким образом введенное число можно преобразовать в дату.
5265079917115 → Sun, 04 Nov 2136 10:11:57 GMT
Римская запись
Римская запись числа, в том случае, если оно меньше чем максимальное для римской записи 3999.
Индо-арабское написание
Запись числа с помощью индо-арабских цифр. Они используются в арабских странах Азии и в Египте.
Азбука морзе
Число, закодированное с помощью азбуки морзе, каждый символ которой представляется в виде последовательсти коротких (точка) и длинных (тире) сигналов.
Хэш-сумма числа, рассчитанная по алгоритму MD5.
Хэш-сумма числа, рассчитанная по алгоритму SHA-1.
Base64
Представление числа в системе Base64, то есть в системе счисления с основанием 64.
QR-код числа
Двумерный штрих-код-картинка. В ней зашифровано введенное число.
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами: