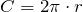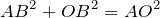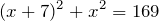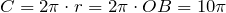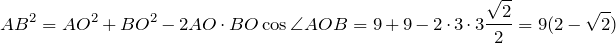Что такое свойства окружности
Окружность
Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.
Часть плоскости, ограниченная окружностью называется кругом.
Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.
Основные термины
Касательная
Прямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Свойства касательной
Хорда
Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.
Свойства хорд
Свойства окружности
Теорема о касательной и секущей
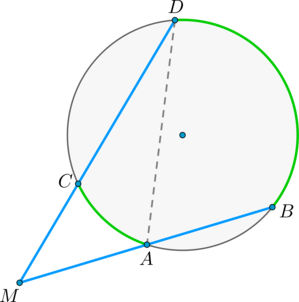
Теорема о секущих
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.
Углы в окружности
Центральным углом в окружности называется плоский угол с вершиной в ее центре.
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Свойства углов, связанных с окружностью
Длины и площади
Вписанные и описанные окружности
Окружность и треугольник
где S — площадь треугольника, а — полупериметр;
Окружность и четырехугольники
Что такое окружность: определение, свойства, формулы
В данной публикации мы рассмотрим определение и свойства одного из основных геометрических объектов – окружности. Также приведем формулы, с помощью которых можно найти ее радиус, диаметр и длину.
Определение окружности
Окружность – это замкнутая кривая на плоскости, состоящая из точек, равноудаленных от определенной точки. Данная точка называется центром окружности.
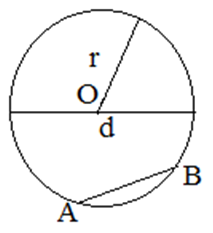
Радиус окружности (R) – это отрезок, соединяющий любую точку, лежащую на окружности, с ее центром.
Диаметр окружности (d) – это линия (хорда), проходящая через центр окружности и соединяющая две противоположные точки, лежащие на ней.
Примечание: Не стоит путать окружность с кругом, т.к. круг – это множество точек плоскости, ограниченных окружностью (т.е. лежащих внутри окружности).
Свойства окружности
Свойство 1
Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.
Свойство 2
Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.
Свойство 3
Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.
Формулы
1. Диаметр окружности (d):
Свойства окружности
Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности.
Отрезок 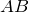
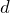
Прямая, имеющая с окружностью одну общую точку, называется касательной. Прямая, имеющая с окружностью две общие точки, называется секущей.
Окружность можно описать вокруг многоугольника и вписать в многоугольник.
Центральный угол окружности – это угол, вершина которого лежит в центре окружности.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на прямой, проходящей через их центры.
Длина окружности вычисляется по формуле
Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
Примеры решения задач
| Задание | Точка 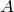 находится от центра окружности на расстоянии находится от центра окружности на расстоянии 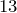 см. Касательная, проведенная из точки см. Касательная, проведенная из точки 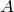 к окружности, на к окружности, на 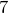 см больше радиуса окружности. Найти длину окружности. см больше радиуса окружности. Найти длину окружности. |
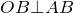 . Рассмотрим прямоугольный треугольник
. Рассмотрим прямоугольный треугольник 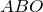 . Пусть
. Пусть 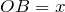 , тогда
, тогда 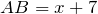 . Запишем теорему Пифагора для данного треугольника:
. Запишем теорему Пифагора для данного треугольника:откуда 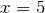
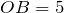
Найдем длину окружности
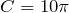
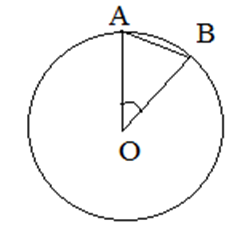
| Задание | В окружности радиуса 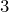 см, центральный угол, опирающийся на хорду см, центральный угол, опирающийся на хорду 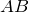 , равен , равен 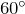 . Найти . Найти 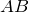 . . |
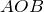 , в котором
, в котором 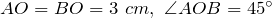 .
.Сторону 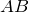
откуда 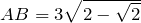
Всё про окружность и круг
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Окружность. Основные теоремы
Определения
Центральный угол – это угол, вершина которого лежит в центре окружности.
Вписанный угол – это угол, вершина которого лежит на окружности.
Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.
Теорема
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Доказательство
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:
1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.
Следствия
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
2. Вписанный угол, опирающийся на полуокружность, прямой.
3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Определения
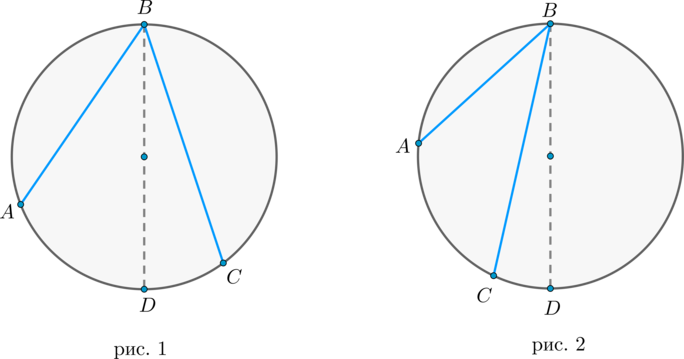
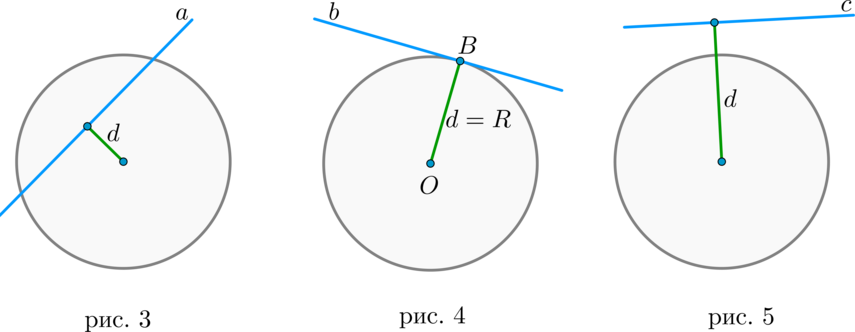
Существует три типа взаимного расположения прямой и окружности:
1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).
2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).
3) прямая \(c\) не имеет общих точек с окружностью (рис. 5).
Теорема
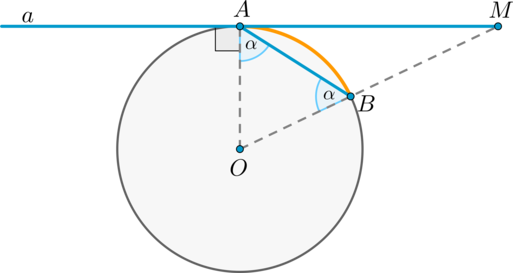
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.
Следствие
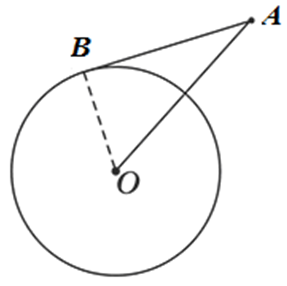
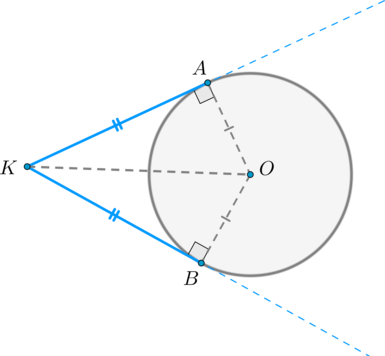
Отрезки касательных, проведенных из одной точки к окружности, равны.
Доказательство
Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\) :
Следствие
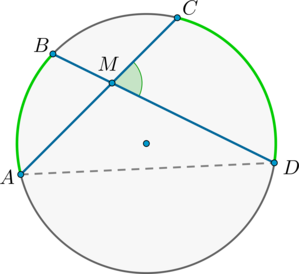
Теорема об угле между секущими
Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.
Доказательство
Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:
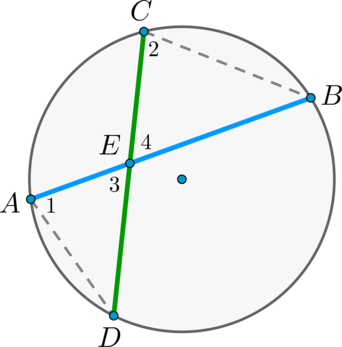
Теорема об угле между пересекающимися хордами
Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: \[\angle CMD=\dfrac12\left(\buildrel\smile\over
Доказательство
\(\angle BMA = \angle CMD\) как вертикальные.
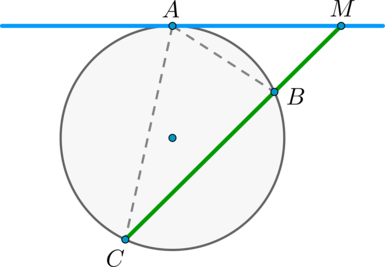
Теорема об угле между хордой и касательной
Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.
Доказательство
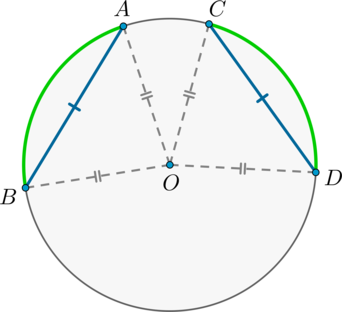
Теорема о дугах, стягиваемых равными хордами
Равные хорды стягивают равные дуги, меньшие полуокружности.
И наоборот: равные дуги стягиваются равными хордами.
Доказательство
Теорема
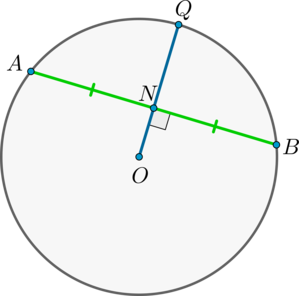
Если радиус делит хорду пополам, то он ей перпендикулярен.
Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.
Доказательство
Теорема о произведении отрезков хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство
Теорема о касательной и секущей
Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.
Доказательство
Следствие