Что такое свойство умножения
Свойства умножения и деления
Свойства умножения
Переместительное свойство умножения
От перестановки множителей произведение не меняется.
Сочетательное свойство умножения
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Переместительное и сочетательное свойства умножения позволяют сформулировать правило преобразования произведений.
При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.
Это свойство справедливо для любого количества слагаемых.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.
В буквенном виде свойство записывается так:
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Свойства деления
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
, где « k » — любое натуральное число.
Обратите внимание, что именно свойство деления выше позволяет нам сокращать дроби.
Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений.
Свойства умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
выражающее переместительное свойство умножения.
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
выражающее сочетательное свойство умножения.
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
Переход от умножения:
соответственно к сложению и вычитанию:
называется раскрытием скобок.
Переход от сложения и вычитания:
называется вынесением общего множителя за скобки.
Свойства умножения и деления
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется.
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
В обратную сторону распределительное свойство умножения относительно сложения звучит так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
В обратную сторону распределительное свойство умножения относительно вычитания звучит так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число.
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?
Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.
Пример 2
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 3
Упростить выражение: 27a – 16a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.
Умножение натуральных чисел: свойства, примеры
Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.
Переместительное свойство умножения натуральных чисел
Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:
Переместительный закон умножения
От перемены мест множителей произведение не меняется.
В буквенном виде переместительное свойство записывается так: a · b = b · a
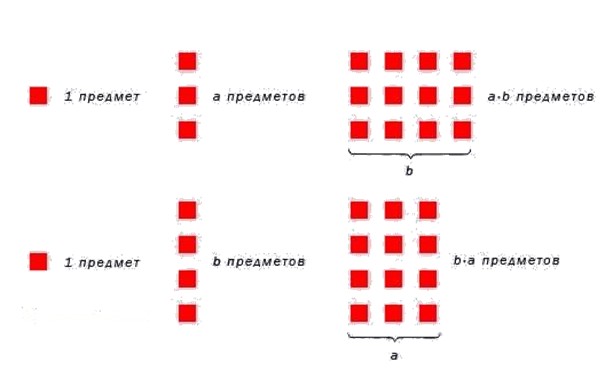
На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.
Сочетательное свойство умножения натуральных чисел
Сочетательный закон умножения
Приведем формулировку в буквенном виде:
4 · 3 · 2 = 4 · 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24
4 · 3 · 2 = 12 · 2 = 12 + 12 = 24
Как видим, теория совпадает с практикой, и свойство справедливо.
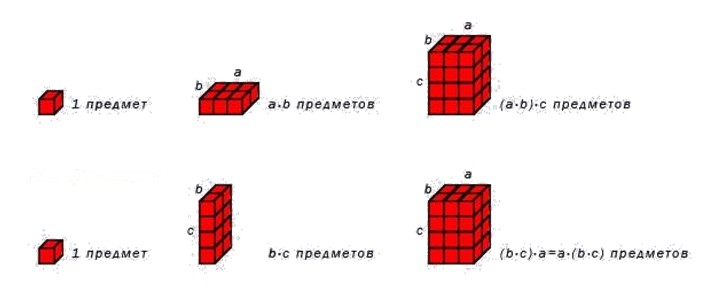
Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.
Распределительное свойство относительно умножения
Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.
Распределительное свойство умножения относительно сложения
Запишем в форме буквенного выражения:
a · b + c = a · b + a · c
4 · 3 + 2 = 4 · 3 + 4 · 2 = 12 + 8 = 20
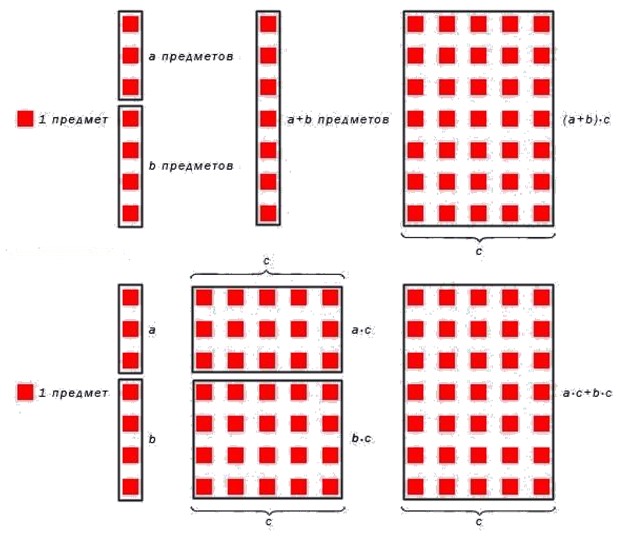
Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.
Распределительное свойство умножения относительно вычитания
Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.
Распределительное свойство умножения относительно вычитания
Запишем в форме буквенного выражения:
В предыдущем примере заменим «плюс» на «минус» и запишем:
Умножение единицы на натуральное число
Умножение единицы на любое натуральное число в результате дает данное число.
По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.
Умножение нуля на натуральное число
Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.
Умножение нуля на натуральное число
По определению, произведение 0 · a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.
В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.
Напимер: 0 · 498 = 0 ; 0 · 9638854785885 = 0
Урок 21 Бесплатно Свойства умножения и деления натуральных чисел
Свойства арифметических операций представляют собой некоторые правила, по которым можно обращаться с числами.
Данные правила часто используют для упрощения различных выражений и при решении различных задач.
Математические операции умножения и деления вам уже хорошо знакомы.
Подробно на примерах рассмотрим основные свойства умножения и деления.
Свойства умножения натуральных чисел
1. Переместительное свойство умножения.
Данное свойство заключается в том, что результат умножения натуральных чисел не зависит от порядка следования множителей.
Переместительное свойство умножения звучит так:
От перестановки множителей местами произведение не меняется.
Данное свойство в буквенной форме выглядит следующим образом:
В этом равенстве переменные а и b принимают любые натуральные значения и нуль.
В качестве примера решим задачу.
Пирожные уложили в коробку в 2 ряда по 3 пирожных.
Определим сколько пирожных всего упаковали, умножим 2 на 3.
2 ∙ 3 = 6 (пирожных) положили в коробку.
Ответ: 6 пирожных.
Если повернуть коробку, то можно заметить другую картину: пирожные в коробке будут уложены в 3 ряда по 2 штуки в каждом ряду.
В таком случае общее количество пирожных найдем так:
3 ∙ 2 = 6 (пирожных) положили в коробку.
Ответ: 6 пирожных.
В первом и во втором случае мы определили, что всего в коробку уложили 6 пирожных, следовательно, выражение 2 ∙ 3 тождественно выражению 3 ∙ 2.
2 ∙ 3 = 3 ∙ 2
2. Сочетательное свойство умножения
Данное свойство заключается в следующем: последовательность действий при умножении чисел не важна.
Сочетательное свойство умножения звучит так:
Произведение трех и более множителей не изменяется, если какую-нибудь группу множителей, стоящих рядом, заменить их произведением.
Данное свойство в буквенном виде выглядит так:
Переменные a, b, c— любые натуральные числа или нуль.
Приведем пример, подтверждающий данное свойство.
В столовую привезли 4 ящика с грушами, в каждом ящике по 2 контейнера в каждом контейнере по 10 груш.
Определим общее количество груш, которые привезли в столовую.
Рассмотрим два варианта решения данной задачи.
Первый вариант решения.
Узнаем сколько всего контейнеров с грушами находится в четырех ящиках, затем определим общее количество груш во всех контейнерах.
Получим следующее числовое выражение: (4 ∙ 2) ∙ 10.
Найдем значение данного выражения.
(4 ∙ 2) ∙ 10 = 8 ∙ 10 = 80 (груш) всего привезли в столовую.
Ответ: 80 (груш).
Второй вариант решения.
Первым делом узнаем сколько всего груш в каждом ящике, т.е. в двух контейнерах (так как в каждом ящике по 2 контейнера).
Полученное значение (количество груш в каждом ящике) умножим на 4 (число ящиков с грушами).
Получим выражение вида: 4 ∙ (2 ∙ 10).
Найдем значение данного выражения.
4 ∙ (2 ∙ 10) = 4 ∙ 20 = 80 (груш) всего привезли в столовую.
Ответ: 80 (груш).
В первом и во втором варианте решения задачи получили одинаковый ответ- 80 груш, что доказывает равносильность первого и второго способа решения данной задачи, следовательно, выражение (4 ∙ 2) ∙ 10 тождественно выражению 4 ∙ (2 ∙ 10).
(4 ∙ 2) ∙ 10 = 4 ∙ (2 ∙ 10)
3. Распределительное свойство умножения.
Распределительное свойство умножения относительно сложения.
Данное свойство связывает две арифметические операции: сложение и умножение.
Формулируется оно так:
Чтобы умножить на число сумму нескольких чисел, можно каждое слагаемое умножить на это число, а полученные произведения сложить.
Это свойство в буквенном виде запишем так:
Данное равенство справедливо для любых натуральных значений a, b, c и нуля.
В этом случае сумма a и b и число с— это множители.
Нам известно, что при перестановке множителей местами произведение не меняется, следовательно, рассмотренное свойство можно сформулировать иначе.
Чтобы любое число умножить на сумму нескольких чисел, можно это число умножить на каждое слагаемое, а полученные произведения сложить.
Для любых натуральных значений a, b, c и нуля справедливо равенство:
Приведем пример подтверждающее данное свойство.
Мороженое стоит 15 рублей.
Покупатель решил расплатиться за три таких мороженных десятирублевыми и пятирублевыми монетами.
Определим стоимость покупки.
За каждое мороженное покупатель должен заплатить 15 рублей.
Пусть он за каждое мороженое отдаст одну десятирублевую монету и пять рублей (10 + 5 = 15).
В таком случае оплатить покупку можно по-разному.
Первый способ оплаты.
Покупатель может достать из кошелька монету в десять рублей и пять рублей за первое мороженное, затем так же за второе, потом за третье.
Данное действие опишем следующим выражением: (10 + 5) ∙ 3.
Найдем значение данного выражения.
(10 + 5) ∙ 3 = 15 ∙ 3 = 45 (руб.) стоимость трех мороженных.
Ответ: 45 (руб.)
Второй способ оплаты.
Покупатель может поступить иначе: сначала вынуть из кошелька 3 десятирублевые монеты, а затем 3 пятирублевые монеты.
В таком случае стоимость трех мороженных будет определяться следующим выражением: 10 ∙ 3 + 5 ∙ 3.
Найдем значение этого выражения.
10 ∙ 3 + 5 ∙ 3 = 30 + 15 = 45 (руб.) стоимость трех мороженных.
Ответ: 45 (руб.)
В первом и во втором случае покупатель, оплачивая три мороженных за каждую по 15 рублей, отдаст 45 рублей.
Следовательно, первое выражение (10 + 5) ∙ 3 и второе выражение 10 ∙ 3 + 5 ∙ 3 равносильны, т.е. справедливо равенство:
(10 + 5) ∙ 3 = 10 ∙ 3 + 5 ∙ 3
Данное свойство позволяет выполнять умножение суммы трех и более натуральных чисел на заданное натуральное число.
У меня есть дополнительная информация к этой части урока!
Распределительное свойство умножения относительно вычитания.
Распределительное свойство умножения справедливо не только относительно сложения, но и относительно вычитания.
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, затем вычитаемое и из первого произведения вычесть второе.
Для любых натуральных чисел a, b, c и нуля верно равенство:
Проверим справедливость распределительного свойства умножения относительно вычитания на примере.
Найдем значение левой части равенства
Вычислим правую часть равенства.
4. Свойство умножения натурального числа на единицу и единицы на натуральное число.
Данное свойство говорит о том, что умножение любого натурального числа на единицу или единицы на любое натуральное число не меняет это число.
Данное свойство звучит следующим образом:
При умножении числа на единицу получается в результате само это число.
При умножении единицы на любое число получится в результате само это число.
Обратите внимание, как выглядит данное свойство в буквенном виде.
а— любое натуральное число.
Рассмотрим пример, подтверждающий данное свойство.
Пусть даны два равенства: 1 ∙ а = а и а ∙ 1 = а.
а = 7
Подставим в первое и во второе равенство вместо буквы а ее значение.
Найдем значение выражения 1 ∙ 7
По смыслу умножения получаем сумму семи единиц (семь раз по единице):
1 ∙ 7 = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7
В таком случае 7 ∙ 1 = 7 (один раз по семь)
Произведение двух множителей, один из которых равен единице, будет равно другому множителю.
Рассмотрим в качестве примера небольшую задачу.
В магазин привезли 5 коробок печенья по 1 килограмму в каждой.
Сколько всего килограммов печенья привезли в магазин?
Известно, что умножение натуральных чисел равно сумме одинаковых слагаемых, причем первый множитель указывает на значение слагаемых, а второй множитель указывает количество таких слагаемых.
Для нашей задачи получаем: пять коробок по килограмму.
1 ∙ 5 = 1 + 1 + 1 + 1 + 1 = 5 (кг) печенья привезли в магазин.
Ответ: 5 (кг).
5. Свойство умножения нуля на натуральное число или натурального числа на нуль.
Произведение натурального числа и нуля равно нулю.
В буквенном виде данное свойство представим так:
а— любое натуральное число и нуль.
Если в произведении нескольких множителей хотя бы один из них равен нулю, то произведение равно нулю.
Рассмотрим простой пример.
Найдем значение выражения 0 ∙ 3.
Произведение 0 ∙ 3 представляет собой сумму трех слагаемых, каждое из которых равно нулю (три раза по нулю).
0 ∙ 3 = 0 + 0 + 0 = 0.
Пройти тест и получить оценку можно после входа или регистрации
Свойства деления натуральных чисел
Рассмотрим основные свойства арифметической операции деления.
У меня есть дополнительная информация к этой части урока!
В отличии от умножения для деления переместительное свойство не выполняется.
Множители мы можем свободно переставлять местами, при этом не меняя результата арифметической операции.
Менять местами делимое и делитель нельзя
a ÷ b ≠ b ÷ a
1. Деление двух натуральных чисел.
Данное свойство подразумевает деление числа на само себя.
Запишем формулировку данного свойства.
Если натуральное число разделить на равное ему число, то в результате получится единица.
С помощью букв свойство запишется так:
а— любое натуральное число.
Убедимся в справедливости данного утверждения на примере.
Мама купила 3 килограмма сахара и расфасовала поровну в 3 пакета.
Сколько килограммов сахара оказалось в каждом пакете?
Так как в каждом пакете одинаковое количество сахара, разделим 3 килограмма сахара на 3 равные части.
Очевидно, что в каждом пакете окажется по одному килограмму сахара.
Запишем решение данной задачи.
3 ÷ 3 = 1 (кг) сахара оказалось в каждом пакете.
Ответ: 1 (кг).
2. Деление натурального числа на единицу.
Доску длиной 3 метра необходимо распилить на равные части.
На сколько частей получится распилить эту доску, если длина каждой части должна быть равной 1 метру?
Если через каждый метр отпиливать часть доски, то в таком случае доску мы распилим на 3 равные части.
Изобразим схематично рисунок для данной задачи.
Запишем решение задачи.
3 ÷ 1 = 3 (части) получится
Ответ: 3 (части).
Свойство деления натурального числа на единицу формулируется следующим образом:
При делении любого натурального числа на единицу получится то же самое натуральное число.
В буквенном виде свойство выглядит так:
а— любое натуральное число.
3. Свойство деления нуля на натуральное число.
Известно, что нуль не является натуральным числом и фактически означает отсутствие чего-либо.
Следовательно, смысл деления нуля на число будет заключаться в следующем:
ноль разделить на число- это значит пустоту (ничего) поделить на части, ясно, что в результате получится нуль (ничего).
Например, поделив 0 конфет между друзьями, каждому другу достанется 0 конфет.
При делении нуля на любое натуральное число в результате получится нуль.
У меня есть дополнительная информация к этой части урока!
Необходимо знать, что натуральное число делить на нуль нельзя!
Представим, что некоторое число а делится на 0, в результате получается некоторое натуральное число b.
а ÷ 0 = b.
Попробуем из этого равенства выразить делимое.
Нам известно, как связаны между собой компоненты операции деления.
Чтобы найти делимое, необходимо частное умножить на делитель.
а = 0 ∙ b.
Если в произведении нескольких множителей хотя бы один из них равен нулю, то произведение равно нулю (данное свойство мы рассмотрели выше).
В результате получим равенство 0 ∙ b = 0, но тогда а получается равным нулю (а = 0).
Однако такого быть не может, так как по условию переменная а— это некоторое натуральное число, а 0 натуральным числом не является.
Следовательно, наши предположения о том, что некоторое натуральное число а может делится на нуль ошибочны, и приводят к противоречию
4. Свойство деления суммы двух натуральных чисел на натуральное число.
Бабушка испекла 4 пирожка с картофелем и 8 пирожков с мясом.
Решила она разделить пирожки поровну четырем своим внукам.
Пирожки можно разделить разными способами, но нужно учитывать тот факт, что каждому внуку должно достаться одинаковое количество пирожков.
Выясним, сколько пирожков досталось каждому внуку.
Рассмотрим два варианта решения данной задачи.
Решение №1.
Можно сначала сложить все пирожки в одну корзинку.
Общее количество пирожков определяется суммой 4 + 8.
Затем все пирожки разделить на четверых внуков поровну.
При этом количество пирожков, которые достанутся каждому внуку опишем выражением (4 + 8) ÷ 4.
Найдем значение данного выражения, для этого определим значение выражения в скобках, далее найденное значение суммы разделим на 4.
(4 + 8) ÷ 4 = 12 ÷ 4 = 3 (пирожка) достанется каждому внуку.
Ответ: 3 (пирожка).
Решение №2.
Сначала разделим на четверых внуков пирожки с картофелем.
Данное действие опишем числовым выражением: 4 ÷ 4.
Затем разделим на всех внуков поровну пирожки с мясом.
Получим числовое выражение 8 ÷ 4.
Найдем сумму пирожков с картофелем и мясом, которые получит каждый внук с помощью выражения (4 ÷ 4) + (8 ÷ 4).
Найдем значение данного выражения.
(4 ÷ 4) + (8 ÷ 4) = 1 + 2 = 3 (пирожка) получит каждый внук.
Ответ: 3 (пирожка).
В первом и во втором решении у нас получился одинаковый результат, по три пирожка получит от бабушки каждый внук.
Следовательно, оба способа решении задачи равносильны, т.е. (4 + 8) ÷ 4 = (4 ÷ 4) + (8 ÷ 4).
Сформулируем свойство деления суммы натуральных чисел на натуральное число.
Чтобы сумму натуральных чисел разделить на какое-нибудь натуральное число, можно сначала найти значение суммы, затем полученный результат разделить.
Справедливо также следующее правило:
Чтобы разделить сумму натуральных чисел на какое-нибудь натуральное число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.
Запишем это свойство деления с помощью букв:
a, b, c— натуральные числа, причем a и b должны делиться на с.
В первой части выполняется действие в скобках, затем деление, в правой части равенства первым делом выполняется деление далее сложение.
Данное свойство позволяет выполнять деление суммы трех и более натуральных чисел на заданное натуральное число.
5. Свойство деления разности двух натуральных чисел на натуральное число.
По аналогии с предыдущим свойством можно выполнять деление разности натуральных чисел на заданное натуральное число.
Запишем формулировку свойства деления разности натуральных чисел на натуральное число.
Чтобы разность натуральных чисел разделить на какое-нибудь натуральное число, можно сначала найти значение разности, полученный результат разделить.
Справедливо также следующее правило:
Чтобы разделить разность натуральных чисел на какое-нибудь натуральное число, можно разделить на это число отдельно уменьшаемое и вычитаемое (если это возможно), а потом из первого частного вычесть второе.
Запишем это свойство деления с помощью букв:
a, b, c— натуральные числа, причем a и b должны делиться на с.
В первом и во втором решении у нас получился одинаковый результат, равный единице.
6. Свойство деления произведения натуральных чисел на натуральное число.
Произведение можно разделить несколькими способами.
Если один из множителей в произведении делится на заданное число (число, на которое необходимо разделить произведение), то возможен еще один вариант деления произведения на число.
В буквенном виде данное свойство выглядит так:
a, b, c— любые натуральные числа.
В качестве примера решим задачу.
Велосипедист каждый день преодолевал 12 километров.
На весь путь ему понадобилось 3 дня.
Сколько километров в день должен проезжать велосипедист, чтобы преодолеть тот же путь за 2 дня?
Чтобы найти ответ на вопрос этой задачи, нужно определить какой путь преодолел велосипедист за 3 дня.
Затем этот путь разделить на 2 (на 2 дня).
12 ∙ 3 (км) преодолел велосипедист за 3 дня.
Произведение 12 ∙ 3 разделим на 2, узнаем сколько ежедневно должен проезжать велосипедист, чтобы преодолеть путь, равный 12 ∙ 3 (км).
Получим следующее числовое выражение для данной задачи:
(12 ∙ 3) ÷ 2.
Найдем значение данного выражения.
Воспользуемся первым способом деления произведения на число.
Найдем значение произведения в скобках (12 ∙ 3), затем полученный результат разделим на 2.
(12 ∙ 3) ÷ 2 = 36 ÷ 2 = 18 (км) в день должен проезжать велосипедист.
Ответ: 18 (км).
Найдем значение выражения вторым способом деления произведения на число.
Сначала разделим 12 на 2, затем полученное частное умножим на 3.
(12 ∙ 3) ÷ 2 = (12 ÷ 2) ∙ 3 = 6 ∙ 3 = 18 (км) в день должен проезжать велосипедист.
Ответ: 18 (км).
Вычисляя значение выражения (12 ∙ 3) ÷ 2 первым и вторым способом получили одинаковый ответ- 18 километров, следовательно, выражение (12 ∙ 3) ÷ 2 равносильно выражению (12 ÷ 2) ∙ 3.
(12 ∙ 3) ÷ 2 = (12 ÷ 2) ∙ 3
Возможен случай, когда один из множителей равен числу, на которое делят произведение.
В результате деления произведения натуральных чисел на заданное натуральное число, которое равно одному из множителей, получается другой множитель.
Запишем буквенный вид данного свойства.
a, b— любые натуральные числа.
Например, если разделить произведение чисел 15 и 2 на 2, то получится:
(15 ∙ 2) ÷ 2 = 15
7. Деление натурального числа на произведение натуральных чисел.
Число можно разделить на произведение двумя способами.
Запишем это свойство деления с помощью букв:
Рассмотрим такую ситуацию.
За 3 двухлитровых банки сока заплатили 600 рублей.
Сколько стоит 1 литр сока?
Разберем два варианта решения данной задачи.
Первым делом можно узнать сколько всего литров сока купили (для этого нужно вычислить произведение 3 и 2), после этого разделить стоимость всей покупки (600 руб.) на количество литров сока в трех двухлитровых банках (3 ∙ 2).
Получим числовое выражение.
600 ÷ (3 ∙ 2).
Найдем значение данного выражения.
600 ÷ (3 ∙ 2) = 600 ÷ 6 = 100 (руб.) стоит 1 литр сока.
Ответ: 100 (руб.)
Сначала можно общую стоимость покупки разделить на количество купленных банок (600 ÷ 3), так мы определим цену одной банки.
Чтобы узнать сколько стоит один литр сока, разделим цену одной банки на количество литров сока в одной банке.
Составим числовое выражение для данной задачи.
(600 ÷ 3) ÷ 2.
Найдем значение данного выражения.
(600 ÷ 3) ÷ 2 = 200 ÷ 2 = 100 (руб.) стоит 1 литр сока.
Ответ: 100 (руб.)
В первом и втором варианте решения задачи получаем одинаковую стоимость одного литра сока, следовательно, будет справедливо равенство:
600 ÷ (3 ∙ 2) = (600 ÷ 3) ÷ 2.
У меня есть дополнительная информация к этой части урока!
Деление обладает еще одним свойством.
Частное не изменится, если делимое и делитель умножить или разделить на одно и тоже натуральное число.
24 ÷ 4 = 6
Разделим делимое и делитель на 2.
(24 ÷ 2 ) ÷ (4 ÷ 2 ) = 12 ÷ 2 = 6
Умножим делимое и делитель на 2.
(24 ∙ 2 ) ÷ (4 ∙ 2 ) = 48 ÷ 8 = 6
Пройти тест и получить оценку можно после входа или регистрации