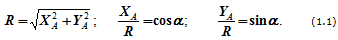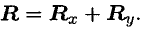Что такое связи и реакции связей

Техническая механика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

2. Связи и реакции связей

Все тела делятся на свободные и связанные.

Свободные тела — это тела, перемещение которых не ограничено.

Связанные тела — это тела, перемещение которых ограничено другими телами.

Тела, ограничивающие перемещение других тел, называют связями.

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.

Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).

Связи делятся на несколько типов.

Связь — гладкая опора (без трения) — реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.

Гибкая связь (нить, веревка, трос, цепь) — груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.

Жесткий стержень — стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.

Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.

Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.

Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.

Неподвижный шарнир. Точка крепления перемещаться не может.

Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (R_x, R_y).

Защемление, или «заделка». Любые перемещения точки крепления невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реактивный момент М_z, препятствующий повороту.

Реактивная сила представляется в виде двух составляющих вдоль осей координат:

Источник

iSopromat.ru

Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.

Реакции связей — это усилия, с которыми связи действуют на данное тело.

Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.

Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

Подробнее про связи и реакции связей смотрите в нашем видео:

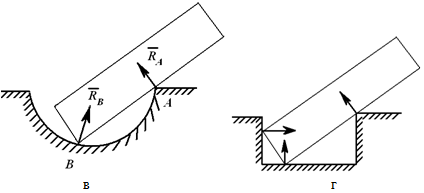
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными. Ниже приведены примеры замены связей их реакциями. На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.

Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1). Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль троса (нити, цепи, стержня) (рисунок 1.2).

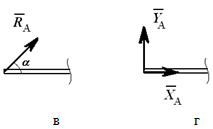
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3, а или 1.3, б). Она может быть заменена либо силой R с углом α (рисунок 1.3, в), либо двумя силами, например, X_A и Y_A (рисунок 1.3, г).

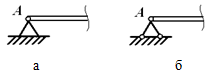
Всегда можно перейти от R и α к X_A и Y_A (и наоборот):

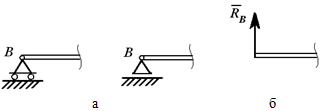
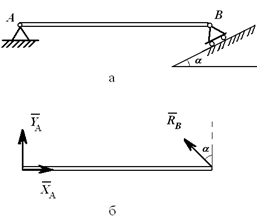
Шарнирно-подвижная опора (рисунок 1.4, а) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности (рисунок 1.4, б).

Связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), их действие заменено силами X_A, Y_A и R_B.

Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросим втулку – получим действие на стержень силы R_D и момента M_D.

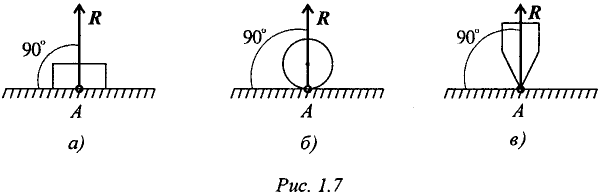
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет момент M_C (рисунок 1.7, б).

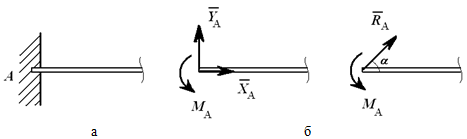
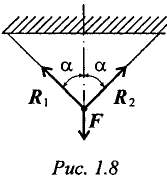
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A с углом α (или X_A и Y_A) и момент Μ_A (рисунок 1.8).

На рисунках 1.9 – 1.15 показаны примеры замены сил, расположенных в пространстве, их реакциями.

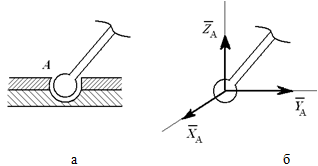
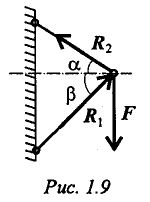
Шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменена системой сил (рисунок 1.9, б) X_A, Y_A и Z_A, т.е. силой, неизвестной по величине и направлению.

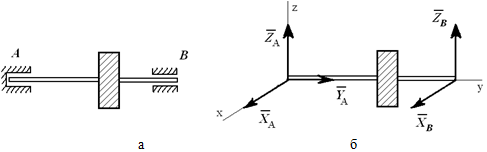
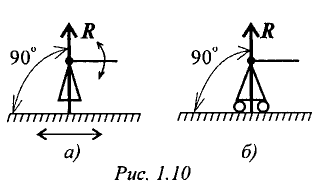
На рисунке 1.10, а показан вал, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами X_A, Y_A, Z_A и X_B, Z_B (рисунок 1.10, б).

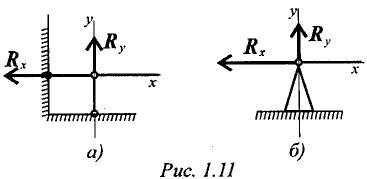
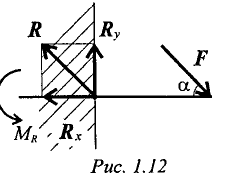
На рисунках 1.11 и 1.12 приведены примеры замены различных связей их реакциями.

Источник

Связи и реакции связей

Связи и реакции связей

Все законы и теоремы статики справедливы для свободного твердого тела.

Все тела делятся на свободные и связанные.

Свободные тела — тела, перемещение которых не ограничено.

Связанные тела — тела, перемещение которых ограничено другими телами.

Тела, ограничивающие перемещение других тел, называют связями.

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей.

Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.

Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей). Все связи можно разделить на несколько типов.

Связь — гладкая опора (без трения)

Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).

Гибкая связь (нить, веревка, трос, цепь)

Груз подвешен на двух нитях (рис. 1.8).

Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.

Жесткий стержень

На схемах стержни изображают толстой сплошной линией (рис. 1.9).

Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.

Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент наложенными на него связями.

Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка 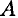опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.

Шарнирная опора

Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.

Подвижный шарнир

Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1.10).

Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной поверхности.

Неподвижный шарнир

Точка крепления перемешаться не может. Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее принято изображать в виде двух составляющих: горизонтальной и вертикальной 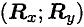(рис. 1.11).

Защемление или «заделка»

Любые перемещения точки крепления невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реактивный момент 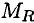, препятствующий повороту (рис. 1.12).

Реактивную силу принято представлять в виде двух составляющих вдоль осей координат

Эта теория взята со страницы решения задач по предмету «техническая механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Связи и реакции связей

Несвободное тело – тело, на перемещения которого в пространстве наложены ограничения.

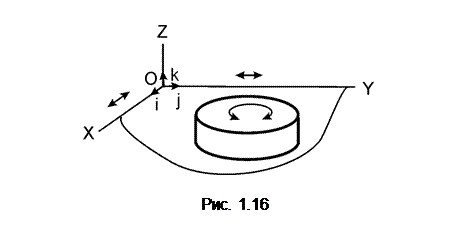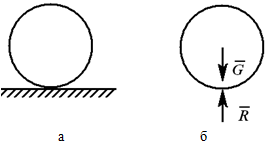
На рис. 1.16 изображено несвободное тело, лежащее на горизонтальной плоскости OXY. Эта плоскость наложила следующие ограничения на перемещения цилиндра: поступательное перемещение, параллельное оси OZ, и повороты относительно осей OX и OY. Плоскость OXY по отношению к телу является связью.

Связи – материальные тела, накладывающие ограничения на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах.

Плоскость OXY (см. рис. 1.16) позволяет цилиндру осуществлять поступательные движения, параллельные координатным осям OX и OY, и поворот в плоскости OXY. Пример несвободного тела – дверь, подвешенная на шарнирах. Связями для двери являются шарниры.

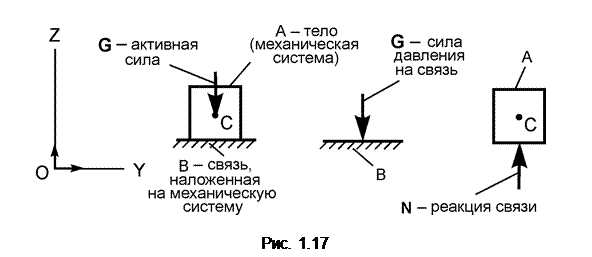
Тело А (рис. 1.17), стремясь под действием силы тяжести G осуществить вертикальное перемещение, которому препятствует связь (тело В), действует на него с некоторой силой, называемой силой давления на связь.

Одновременно (по аксиоме 5) связь действует на тело с такой же по модулю, но противоположно направленной силой N: N = – G. Силу N называют реакцией связи. Реакции связей относятся к разряду внешних сил.

Реакции связей – силы, действующие на точки механической системы со стороны материальных тел, осуществляющих связи, наложенные на эту систему.

В дальнейшем силы, не являющиеся реакциями связей, называют активными силами. Активные силы, как и реакции связей, относятся к разряду внешних сил. Особенностью активной силы является то, что её модуль и направление непосредственно не зависят от других, действующих на тело сил. Реакция связи зависит от действующих на тело активных сил и заранее неизвестна. Если на тело не действуют активные силы, то реакции связей равны нулю.

Для определения величин реакций связей надо решить соответствующую задачу статики. Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Если связь одновременно препятствует перемещениям тела по нескольким направлениям, то направление реакции связи заранее неизвестно и должно определяться при решении конкретной задачи.

Рассмотрим подробнее, как направлены реакции основных видов связей.

Гладкая связь – материальное тело, имеющее поверхность, силами трения о которую рассматриваемой механической системы пренебрегают.

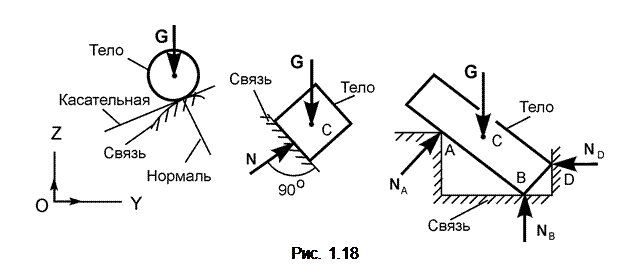
Такая поверхность не дает телу перемещаться только по направлению общего перпендикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис. 1.18).

Реакция N гладкой поверхности направлена по общей нормали к поверхности соприкасающихся тел в точке их касания и приложена в этой точке со стороны связи.

Когда одна из соприкасающихся поверхностей является точкой или линией, то реакция этой связи направлена по нормали к другой поверхности. Зачастую реакцию N называют нормальной реакцией.

Гибкая связь – нерастяжимые нить или трос, вес которых не учитывают.

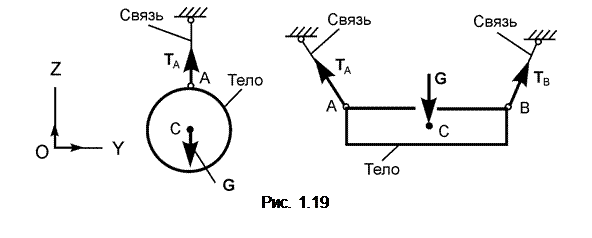На рис. 1.19 изображены тела (механические системы), на которые наложены гибкие связи (нити).

Реакции Т_А, Т_В натянутых нитей направлены вдоль нитей от тела к точкам подвеса нитей.

Невесомый стержень – недеформируемый стержень, загруженный только по его концам.

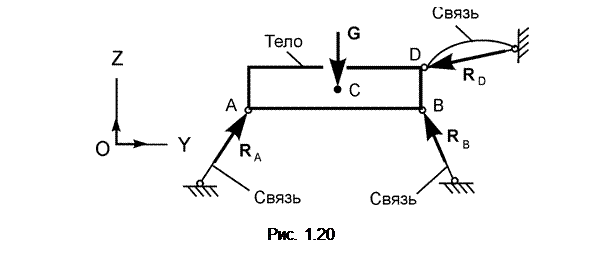
Невесомый стержень соединяется с телом и опорой шарнирно. На рис. 1.20 изображена балка, опирающаяся на три невесомых стержня.

При этом один стержень прямой, а остальные изогнуты. Реакция невесомого стержня направлена по линии, соединяющей концы стержня. Прямой стержень работает только на растяжение или сжатие.

Дата добавления: 2015-05-30 ; просмотров: 4305 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Лекция 2. Связи и их реакции

2.1. Понятие о связях

В Лекции 1 были даны определения свободных и несвободных тел. Возможное движение таких тел, соответственно, ничем не ограничено или же, наоборот, стеснено другими телами. Любые ограничения, накладываемые на движение тела, называют связями. Как правило, связи реализуются с помощью других тел.

Пример. Для лежащего на столе карандаша стол служит связью – он не дает карандашу падать вниз.

Пытаясь двигаться, тело вступает с наложенной на него связью в механическое взаимодействие и действует на нее с силой, которую называют силой давления на связь. Согласно закону равенства действия и противодействия, связь действует на тело с силой, равной по модулю, но противоположной по направлению. Сила, с которой связь действует на тело, называется силой реакции или реакцией связи. Она направлена в сторону, противоположную той, куда связь мешает телу двигаться. В более сложных случаях связь описывается не одной силой, а системой сил.

В теоретической механике применяется принцип освобождаемости от связей:

Пример. Карандаш, лежащий на столе, под действием силы тяжести \(\vec G\) должен двигаться вниз. Этого не происходит, потому что на карандаш действует реакция стола \(\vec N\), направленная вверх и уравновешивающая силу тяжести (рис. 2.1).

Рис. 2.1. Карандаш под действием силы тяжести и реакции связи

Как правило, проектируемые сооружения, конструкции и механизмы не «плавают свободно» в пространстве; их перемещения стеснены какими-то связями. Поэтому поиск реакций связей, наложенных на тело, – важная задача. Знать реакции связей, наложенные на тело, необходимо по двум причинам:

Требуется знать, выдержит ли связь давление, оказываемое на нее телом. Это давление равно реакции, которую развивает связь.

Пример. Мосты и путепроводы могут выдерживать строго определенную нагрузку, поэтому на них устанавливают ограничения по массе въезжающих автомобилей и устанавливают соответствующие дорожные знаки (рис. 2.2). В этом примере мост служит связью для изучаемого твердого тела (автомобиля).

Пример. Спускаемые модули космических кораблей проектируют таким образом, чтобы они выдерживали жесткую посадку (удар о Землю). При ударе на эти модули действует сила реакции Земли, не дающей им падать дальше.

2.2. Простейшие виды связей

Ниже рассматриваются некоторые виды связей и указываются направления их реакций.

Гладкая поверхность (опора). Будем называть гладкой поверхность, трением о которую можно пренебречь. Реакция \(\vec N\) этой связи направлена перпендикулярно поверхности. Это объясняется тем, что при движении вдоль гладкой поверхности сопротивления не возникает; зато связь мешает телу «проваливаться» внутрь поверхности. Если поверхность искривлена, то сила ее реакции направлена перпендикулярно к касательной плоскости (рис. 2.3).

Рис. 2.3. Направление реакции плоской горизонтальной, плоской наклонной и искривленной поверхности

Замечание. Соприкосновение тела и поверхности может происходить не в единственной точке, а на некоторой площадке. Это значит, что действие тела на поверхность (как и ее реакция) будут представлять собой распределенную силу. Для простоты вычислений ее заменяют сосредоточенной равнодействующей.

Из-за того, что вектор \(\vec N\) направлен перпендикулярно (по нормали) к поверхности, эту реакцию также называют нормальной.

Пример. Гладкой поверхностью можно считать стол, на котором покоится некий предмет, например, карандаш (см. рис. 2.1).

Если одна поверхность опирается на другую своим ребром (изломом), то направление реакции перпендикулярно той поверхности, к которой в месте контакта можно провести касательную. Так, на рис. 2.4 а) показаны реакции поверхности в двух точках – A и B. Если же обе поверхности в месте соприкосновения имеют излом, как в точке A на рис. 2.4 б), то направление реакции нельзя определить заранее.

Однако положение равновесия, подобное рис. 2.4 б), крайне неустойчиво. Если представить себе, что на рисунке изображена балка, положенная на бордюр, то она упадет при малейшем сотрясении. Поэтому указанный случай представляет, скорее, теоретический интерес.

Нить. Представление о такой связи дает леска, на которой подвешен груз. Нить предполагается невесомой, гибкой (она может сминаться), тонкой и нерастяжимой (сохраняющей свою длину). Эпитет «тонкая» означает, что ее толщина много меньше длины, и поэтому свойства нити одинаковы во всех точках ее поперечного сечения. Такая связь препятствует движению тела лишь в одном направлении – вдоль по нити в сторону ее растяжения. Поэтому реакция данной связи (натяжение \(\vec T\)) направлена вдоль нити в сторону точки подвеса (рис. 2.5).

Рис. 2.5. Направление натяжения нити

Пример. На груз маятника действуют две силы: тяжести \(\vec G\) и натяжения нити \(\vec T\) (рис. 2.6). Согласно правилу параллелограмма, они имеют равнодействующую, которая в положении, указанном на рисунке, направлена вниз и налево. Поэтому маятник, выведенный из вертикального положения и предоставленный сам себе, начнет двигаться в обозначенную сторону.

Цилиндрический шарнир (подшипник). Эта связь соединяет два тела так, что одно может вращаться относительно другого вокруг оси, называемой осью шарнира. Считается, что реакция \(\vec R\) шарнира лежит в плоскости, перпендикулярной его оси; но заранее определить направление реакции в этой плоскости, как правило, нельзя. Дело в том, что подобное закрепление тела не позволяет ему двигаться в любом направлении, перпендикулярном указанной оси.

Пример. Соединение двери и косяка с помощью петель (рис. 2.7) можно считать шарниром. Действительно, прикладывая усилие, перпендикулярное оси вращения, нельзя «сдернуть» дверь с петель, не повредив косяка.

В двух предыдущих случаях (опора и нить) задача об определении реакции связи содержала одну неизвестную величину – модуль (числовое значение) реакции. В случае цилиндрического шарнира искомых величин две – надо узнать еще и направление реакции в плоскости вращения. Но выбирают неизвестные разными способами, в зависимости от удобства.

Во-первых, можно искать модуль реакции R и угол α, образуемый данным вектором с какой-либо прямой в плоскости вращения. Если ввести в этой плоскости систему координат, этой прямой может быть, например, ось абсцисс, как на рис. 2.8 а). Во-вторых, можно разложить искомый вектор \(\vec R\) на две составляющие, направленные вдоль осей координат, как на рис. 2.8 б). Тогда потребуется найти числовую величину каждой из составляющих.

Рис. 2.8. Тело AB закреплено в точке А с помощью цилиндрического шарнира

Сферический шарнир соединяет тела так, что они могут вращаться друг относительно друга вокруг одной точки – центра шарнира (рис. 2.9).

Указанная точка не может совершить никакого перемещения относительно обоих тел. Поэтому реакция сферического шарнира в пространстве может иметь любое направление. Аналогично цилиндрическому шарниру, при решении задач эту реакцию часто раскладывают на три компоненты, направленные вдоль координатных осей (рис. 2.10).

Рис. 2.10. Сферический шарнир A реагирует на тело AB с силой \(\vec R\), которая раскладывается на компоненты \(\vec X_\), \(\vec Y_\) и \(\vec Z_\)

Частным случаем сферического шарнира является подпятник – подшипник с упором. Его схематичное изображение представлено на рис. 2.11.

Рис. 2.11. Тело AB в точке A связано подпятником

Реакция подпятника также имеет произвольное направление в пространстве.

Подвижный шарнир. Конструктивно эта связь представляет собой цилиндрический или сферический шарнир, соединяющий тело с некоторой поверхностью и способный перемещаться по ней. Такая способность может достигаться водружением шарнира на катки (из-за чего его также называют опорой на катках). Поскольку шарнир не препятствует движению тела вдоль поверхности, его реакция направлена перпендикулярно ей (рис. 2.12).

Рис. 2.12. Реакция подвижного шарнира

Пример. Подвижные шарниры могут использоваться при строительстве металлических мостов. Если оба конца такого моста закрепить неподвижно, то летом, удлинняясь при повышении температуры, мост будет выгибаться дугой (рис. 2.13 а). Зимой при охлаждении конструкция станет сужаться, пытаясь сорвать крепления (рис. 2.13 б).

Рис. 2.13. Металлический мост при нагревании и охлаждении

Такие деформации малозаметны, но, повторяясь из года в год, они могут не только привести в негодность дорожное покрытие, но и вызвать разрушение самого моста. Поэтому один из неподвижных шарниров заменяют подвижным (рис. 2.14). Это дает мосту возможность растягиваться и сжиматься без катастрофических последствий.

C математической точки зрения подвижный шарнир полностью аналогичен опоре: реакции обеих связей перпендикулярны рассматриваемой поверхности. Тем не менее, из-за его конструктивных особенностей подвижный шарнир лучше рассматривать отдельно.

Невесомый стержень служит для соединения двух тел; предполагается, что к обоим телам он прикреплен шарнирами (как правило, сферическими, если тела рассматриваются в пространстве, и цилиндрическими, если речь идет о плоской задаче). Аналогично нити, толщина стержня обычно много меньше его длины, и ее не берут в расчет. Кроме того, как понятно из названия, весом такого стержня по сравнению с наложенной на него нагрузкой можно пренебречь.

Замечание. «Невесомость» стержня – это очередная идеализация. Металлические стержни, составляющие каркас многих строительных конструкций, могут иметь массу в десятки и сотни килограммов (соответственно, их вес может составлять тысячи ньютонов). Но они воспринимают нагрузку во много раз большую: например, достаточно сравнить массу металлической арматуры со всей массой железобетонной плиты. Поэтому весом стержней зачастую пренебрегают.

Реакция \(\vec S\) прямого невесомого стержня, имеющего шарнирное закрепление, направлена вдоль самого стержня. Действительно, пусть стержень AB соединяет два тела: AC и BC (рис. 2.15).

Рис. 2.15. Определение направления реакции прямого стержня

Это значит, что к нему приложены две силы – в точках A и B. Поскольку стержень неподвижен, они находятся в равновесии. Согласно первой аксиоме статики, это значит, что эти силы направлены вдоль стержня. По закону равенства действия и противодействия, стержень реагирует на это воздействие с силой, равной по модулю, но противоположной по направлению. Поэтому реакция также направлена вдоль стержня.

Рассуждая аналогичным образом, легко показать, что реакция криволинейного шарнирно закрепленного стержня направлена вдоль хорды, соединяющей его концы (рис. 2.16).

Рис. 2.16. Определение направления реакции изогнутого стержня

Следует учитывать, что имеется два возможных направления реакции данной связи; выбор конкретного направления зависит как от состояния, в котором находится стержень, так и от того, в каком из концов тела эта реакция рассматривается. Так, выше на рис. 2.15 и рис. 2.16 изображены случаи, в которых стержень сжат (например, он удерживает плиту BC от падения на горизонтальную поверхность AC). Противодействуя этому сжатию, он стремится растянуться, поэтому реакция \(\vec S\) в точке B направлена в сторону от стержня. Если стержень растянут (например, он скрепляет тела AC и BC, а мы стараемся оторвать одно тело от другого), то он попытается сжаться, и направление вектора \(\vec S\) следует изменить на противоположное – развернуть его внутрь стержня.

Иногда можно рассматривать стержень как результат отвердевания нити. Например, с точки зрения теоретической механики безразлично, как груз маятника соединяется с часовым механизмом: с помощью тонкой нити или стержня. Тем не менее, между двумя этими связями существует разница. В отличие от нити, стержень не может сминаться. Кроме того, направление реакции нити определено однозначно, а реакция стержня может быть направлена двумя разными способами.

Существуют и другие виды связей, которые будут рассмотрены в Лекции 3.

2.3. Тело на гладкой наклонной плоскости

Ниже мы рассмотрим простой, но важный пример, на котором покажем последовательность решения задач о равновесии твердого тела.

Пусть груз веса P находится на гладкой плоскости, наклоненной к горизонту под углом α, и удерживается нитью, натянутой вдоль самой поверхности. Требуется найти реакцию плоскости N и натяжение нити T. Параметр α может меняться в пределах от 0° до 90°.

Разобьем решение на несколько этапов.

Выберем тело, равновесие которого будет рассматриваться (в нашем случае – груз) и сделаем первоначальный чертеж (рис. 2.17)

Изобразим силы, действующие на выбранное тело. В нашем случае на груз действует сила тяжести \(\vec G\), направленная вертикально вниз и численно равная его весу P. Движение груза ограничено двумя связями – поверхностью и нитью. Согласно принципу освобождаемости от связей, их можно отбросить, заменив реакциями – нормальной реакцией \(\vec N\) и натяжением \(\vec T\), соответственно (рис. 2.18).

Составим условия равновесия. Поскольку система сил, действующих на тело, сходится (мы пренебрегаем размерами груза), то условие равновесия выражается единственным векторным равенством:

Введем систему координат так, как показано на рис. 2.19: ось x направим параллельно поверхности, ось y – перпендикулярно ей.

Спроецируем обе части равенства (2.1) на оси координат и получим систему линейных уравнений относительно неизвестных N и T:

При нахождении проекций мы воспользовались известным из планиметрии фактом: если соответственные стороны двух углов перпендикулярны, то эти углы равны. Фактически это утверждение означает, что один угол получается из другого поворотом на 90° и последующим переносом в другое место на плоскости.

Горизонтальная прямая перпендикулярна линии действия силы \(\vec G\), оси x и y также перпендикулярны. Поэтому угол между вектором \(\vec G\) и отрицательным направлением оси y равен углу α между горизонтальной прямой и осью x.

В более сложных задачах, в которых к телу прикладывается большое количество сил, можно оформлять вычисление проекций на координатные оси в виде таблицы:

Уравнения в проекции на ту или иную ось получаются суммированием (с учетом знаков) всех слагаемых в соответствующей строке таблицы.

Решим полученную систему и проанализируем решение. Из (2.2) получаем, что T = P sin α, N = P cos α. Тем самым, реакции связей найдены; выясним, как они ведут себя в зависимости от угла α. При α = 0° получаем N = P, T = 0, что согласуется с чисто физическими соображениями: если опорная поверхность горизонтальна, то она полностью воспринимает вес груза, а удерживающая нить остается ненатянутой. При α = 90° (вертикальная поверхность) N = 0, T = P, т.е. груз удерживается только нитью, а поверхность его движению не препятствует.

В общем случае, если убрать нить (положить T = 0 независимо от веса P), то груз не будет находиться в равновесии. Действительно, проекция вектора \(\vec G+\vec N\) на ось y равна нулю, а на ось x она составляет –P sin α. При α ≠ 0° эта проекция меньше нуля, а значит, тело станет двигаться в сторону, противоположную оси y (вниз).

Из нашего решения и закона равенства действия и противодействия следует, что сила давления груза на опорную плоскость равна P sin α, а на нить – P cos α. Если максимально допустимые для опоры и нити нагрузки меньше указанных значений, то связи не выдержат указанного давления: плоскость может деформироваться или разрушиться, а нить – оборваться.

Замечание. Направление координатных осей выбирается из соображений удобства. Как правило, они проводятся параллельно или перпендикулярно неизвестным реакциям. Это сводит к минимуму число неизвестных проекций; тем самым, уравнения типа (2.2) упрощаются. Оси координат можно было бы провести и каким-либо другим образом. Например, ось x можно было бы направить по горизонтали направо, а ось y – вертикально вверх; их можно было бы ориентировать относительно сил совершенно произвольным образом. Конечный ответ задачи при этом бы не изменился, но нахождение проекций и последующее решение системы уравнений усложнилось бы. Приемы упрощения уравнений равновесия с помощью выбора системы координат излагаются далее в п. 4.3.

Вопросы для самоконтроля

Груз располагается на конце невесомого стержня, который с помощью цилиндрического шарнира закреплен в неподвижной точке A. Стержень отклонили от вертикали на угол α (рис. 2.20). При каких значениях α груз будет находиться в равновесии? Что изменится, если заменить стержень нитью?

Задачи к лекции

Лампа веса 40 Н подвешена к потолку на двух одинаковых цепочках длины 26 см каждая. Расстояние между точками их подвеса составляет 40 см (рис. 2.21). Найти натяжение каждой из цепочек.

Прибор веса 1200 Н хотят установить на легкую треногу, каждая из ножек которой имеет длину 2 м. В рабочем состоянии основания ножек образуют правильный треугольник со стороной 1 м (рис. 2.22). Выдержит ли тренога нагрузку, создаваемую прибором, если каждая из ее опор рассчитана на максимальную нагрузку 380 Н?

Ответы. 1. 52 Н. 2. Не выдержит: нагрузка на каждую опору составит около 417.79 Н.

Также рекомендуется решить задачи из §§1, 2, 6 [2].

Источник