Что значит скидка 10 процентов в математике
Как решать задачи с процентами
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100, как в примере выше.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
А вот, как перевести проценты в десятичную дробь — обратным действием:
Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а потом используем предыдущее правило:
Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
38/0,16 = 38 * 100/16 = 237,5
Значит 237 задачи включили в этот сборник.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: возьмем алгоритм из правила выше:
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
В классе учится 10 девочек — это 40%.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
Формула расчета процента от числа выглядит так:
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?
Как решаем: подставим в формулу данные из условий задачи.
110 * (1 + 12/100) = 110 * 1,12 = 123,2.
Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
Формула расчета выглядит так:
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
Как решаем: подставим в формулу данные из условий задачи.
75 выпускников закончат школу в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?
Как решаем: подставим в формулу данные из условий задачи.
5000 * (1 + 12 * 15/100) = 14000
Родители через год внесут в банк 14000 рублей.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.
Как решаем: просто подставим в формулу данные из условий задачи:
25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.
Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!
Способы нахождения процента
Универсальная формула для решения задач на проценты:
| A * b = C, где A — исходное число, b — проценты, переведенные в десятичную дробь, C — новое число. |
Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.
Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.
Деление числа на 100
При делении на 100 получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать процент от суммы, нужно умножить их на размер 1%. А чтобы перевести известное значение, следует разделить его на размер 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Пропорция — определенное соотношение частей между собой.
С помощью метода пропорции можно рассчитать любые %. Выглядит это так:
Читается: a относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Ответ: купить спортивную футболку выгоднее на 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Задачи на проценты с решением
Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.
Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
76 : 100 = 0,76 — 1% от массы человека
Ответ: масса воды 53,2 кг
Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?
Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.
Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:
После двух понижений изменение цены составит:
Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.
Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?
По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто
Получается, что стоимость одной пары брюк — это 23% стоимости пальто.
Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.
Ответ: пять пар брюк на 15% дороже, чем одно пальто.
Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.
По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.
Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.
Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.
А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.
Ответ: заработок жены составляет 27%.
Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.
Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.
На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.
Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.
Как посчитать скидку в процентах: основные способы и приемы при решении
Каждый раз, увидев скидку в магазине, люди воспринимают ее как выгодное предложение. Однако для того, чтобы принять наиболее рациональное решение, иногда требуется рассчитать размер экономии в процентах. Умение узнать, сколько составляет скидка на тот или иной продукт, может помочь каждому в повседневной жизни.
Известны начальная стоимость и размер скидки в рублях

Как посчитать, сколько процентов скидка, если известны начальная стоимость и размер скидки? Иными словами, нужно определить, на какую долю была уменьшена цена продукта.
Существует два основных метода, как посчитать размер скидки в процентах.
Например: футболка стоила 500 рублей, во время скидок она подешевела на 100 рублей.
Вывод: экономия при покупке составила 20 процентов.
Второй способ, вероятно, более сложен для понимания, но содержит всего одно действие, так что шанс ошибиться в вычислениях минимален. Однако, если изучить этот принцип, задачи на выявление экономии больше никогда не будут вызывать затруднения.
Для получения результата нужно поделить сумму скидки на цену продукта или вещи, а затем умножить полученное значение на 100 %. Например: упаковка яиц стоила 60 рублей, а потом ее цена была снижена на 15 рублей.
Вывод: экономия составила 25 процентов.
Известны начальная и конечная стоимости
Как посчитать скидку в процентах, зная начальную и конечную стоимость? Существует два пути решения.
Во-первых, можно узнать размер скидки, отняв конечную стоимость от начальной. Далее решать задачу так же, как описано в первой части статьи.
Например: футболка стоила 500 рублей, а теперь ее продают за 400.
Вывод: экономия составила 20 %.
Во-вторых, можно рассчитать, сколько процентов от начальной цены составляет цена со скидкой, а потом отнять это значение от 100 %.
Например: упаковка яиц стоила 60 рублей, а потом ее цена была снижена до 45.
Вывод: скидка на покупку упаковки яиц составила 25 процентов.
Теперь при покупке вы сможете посчитать скидку в процентах.
Задачи на вклады и скидку
Прежде чем перейти к задачам на вклады и скидки, необходимо разобраться зачем вообще люди кладут деньги в банк и как найти выгодную скидку.
Задачи по вкладам
Естественно, люди кладут деньги в банк (открывают вклад), не по доброте душевной. Вклады открываются с целью получения прибыли. Банк предлагает следующее: вы кладёте в банк определённую сумму на определённый срок.
Например, на год. В течение года вы не сможете воспользоваться своими деньгами (ими будет пользоваться банк), но за это банк вам заплатит, вернув через год не только вложенную вами сумму, но и небольшое вознаграждение.
Какова будет сумма вознаграждения?
Для её нахождения банк устанавливает процент годовых. Если вы умножите сумму вашего вклада на процент годовых, вы найдёте, какое вознаграждение добавит банк к вашему вкладу.
Рассмотрим задачи на эти темы из учебников Петерсона и Виленкина.
Задача из Петерсона
Вкладчик внес в банк 1200 р. В какую сумму вклад превратится через год, если банк начисляет доход в размере 4% годовых?
4% = 0,04
1200 · 0, 04 = 48 р. — такое вознаграждение доложит банк вкладчику через год.
Теперь найдем общую сумму, которую заберет вкладчик через год.
1200 + 48 = 1248 р. — в такую сумму превратится вклад через год.
Ответ: 1248 р. — в такую сумму превратится вклад через год.
Задачи на скидку (уценку)
Скидка — это понижение цены товара или услуги. Чаще всего скидку указывают в процентах. Поэтому, чтобы найти на сколько в рублях понизилась цена товара, нужно цену товара умножить на процент скидки.
Задача из ГИА 9 класс
Найдем скидку в рублях.
10% = 0,1
5000 · 0,1 = 500 р. — скидка в рублях.
Теперь найдем цену товара с учетом скидки.
5000 − 500 = 4500 р. — цена товара с учетом скидки.
Ответ: 4500 р. — цена товара с учетом скидки.
Как считать скидки в процентах самостоятельно и при помощи Excel
Еще со школьной скамьи нам знакомо такое понятие, как процент. Сегодня мы можем встретить проценты в виде скидки в торговых магазинах, надбавки к заработной плате, кредитных платежей, комиссии за перевод денежных средств, доли акций в компании.
Наверняка многие из вас интересуются тем, как посчитать процент скидки от цены. Это несложный расчет, для которого требуются знания математики средней школы.
Как считать скидки в процентах?
Для этого необходимо вспомнить школьную пропорцию «крест-накрест». Так, 100 % составляют полную стоимость товара, каждый процент является долей от стоимости.
Чтобы рассчитать скидку в процентах, необходимо умножить сумму товара на процент скидки и поделить на 100: C = A*B/100.
Примеры из реальной жизни
Как считать скидки в процентах?
Представим, что в магазине хозяйственных товаров каждую субботу проводится акция в виде скидки на все товары в размере 30 %. Так, например, вы сможете приобрести швабру с интересным дизайном за 2380, а не за 3400 рублей, получив экономию в размере 1020 рублей:
С = 3400*30/100 = 1020 рублей.
Приходя в ресторан, принято оставлять чаевые в размере 5-10 % от суммы заказа. Как посчитать сумму чаевых, если вы сделали заказ на 1000 рублей?
X = 1000*10/100 = 100 рублей
Лучше оставлять на чай круглую сумму. Если у вас получилось 107 или 127 рублей, то оставьте 110 или 130 рублей.
Представьте, что ежегодно сумма интересующего вас товара увеличивается на 5 %. Например, клюквенный лимонад с листочками мяты в этом году стоит 60 рублей. Сколько вы за него заплатите в следующем году?
C = A*B/100 = 60*5/100 = 3 рубля.
Сумма лимонада составит: 60 + 3 = 63 рубля.
Можно и другим способом произвести расчет: 60*(1+60*0,05) = 63 рубля.
Чтобы понять, что означает 0,05 в этой формуле, необходимо знать, что 1 % от 100 % составляет 0,01 или, иначе, это равняется 1/100 = 0,01. Так можно поделить любое интересующее вас число на 100 и получить результат.
Это аналогичный вариант расчета, позволяющий сэкономить ваше время и листы бумаги.
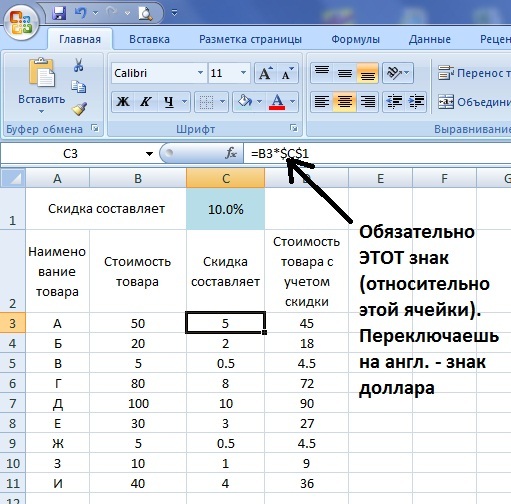
Скидки в процентах в Excel
Как считать скидки в процентах?
Для упрощения расчетов в больших объемах данных можно воспользоваться инструментами Excel. Для этого необходимо произвести аналогичные записи в каждый столбец и запустить копирование формулы с сохранением определенных столбцов и строчек. Для фиксации используется знак доллара. Для этого необходимо переключить клавиатуру на английский язык. Расчет в Excel позволяет автоматизировать работу, сделать все грамотно, последовательно, без ошибок.
Теперь вы с легкостью можете понять, как считать скидки в процентах не только самостоятельно с использованием листа бумаги, ручки и калькулятора, но и при помощи умного помощника Excel. Если перед вами стоит расчет одного показателя, то, конечно, проще воспользоваться ручкой и бумагой или посчитать в голове. Если же вы оперируете большой базой данных и не хотите вручную считать каждое число, то Excel придет вам на помощь.
У вас остались какие-то вопросы? Можете поделиться своими способами расчета процента скидки от товара в комментариях или предложить интересные задачи для размышления.
Как находить проценты от числа
Основные определения
Процент — это одна сотая часть от любого числа. Обозначающим знаком является %.
Чтобы узнать, как перевести проценты в десятичную дробь, нужно убрать знак % и разделить известное на 100. Например, 18% — это 18 : 100 = 0,18.
А если нужно перевести натуральное число или десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например, 0,18 = 0,18 · 100% = 18%.
Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а далее используем предыдущее правило и переведём десятичную дробь в проценты.
Проценты: правила
Рассмотрим четыре известных способа поиска процентов.
Занимайтесь математикой в удовольствие вместе с нашими преподавателями на онлайн-курсах по математике для детей и подростков!
Нахождение одного процента от числа
Найти процент от числа можно несколькими способами.
Первый способ
Найдем, чему равен 1%.
Умножим полученное значение на количество искомых процентов.
Пример: найти 12% от числа 48.
Второй способ
Переведем проценты в десятичную дробь.
Умножим число на полученную десятичную дробь.
Давайте снова найдем 12% от 48, но другим способом.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Как решаем:
250 : 100 = 2,5 — это 1% от стоимости шоколада,
значит, 2,5 × 15 = 37,5 — это 15%.
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Равенство двух отношений называют пропорцией.
a : b = c : d или a/b = c/d
Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Как решаем:
Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию:
1390 руб. = 100%
x руб. = 14%
Перемножим крест-накрест и найдем x:
x = 1390 × 14 : 100
x = 194,6
Ответ: выгода по скидке составила 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.
| Процент | Дробь | Как найти % от числа a |
|---|---|---|
| 10% | 1/10 | a : 10 |
| 20% | 1/5 | a : 5 |
| 25% | 1/4 | a : 4 |
| 50% | 1/2 | a : 2 |
| 75% | 3/4 | a : 4 × 3 |
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
значит, нужно заплатить 75% от первоначальной цены.
75% — это 3/4 от числа, значит,
8500 : 4 × 3 = 6375 (рублей).
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Онлайн-калькулятор
Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так: