нарисованная шахматная доска при касании оказалась терминалом для ввода трехзначного кода
Шахматные задачки. Шахматная доска
Продалжаю решать задачки и знакомиться с языком Python на Питонтьютор. Попалась задачка которая мне очень понравилась и заставила попотеть. Условие:
И тут меня понесло куда-то не туда. Код конечно заработал, но он оказался так далек от совершенства. После решения мне стал доступен код разработчиков задачи, глянув на него я моментально понял принцип его работы и ведь я мог догадаться. Я должен был догадаться! Все было так просто и изящно. Но. У меня получилось как получилось. Обо всем по порядку.
Я рассуждал так. На шахматной доске клетки располагаются в следующей последовательности, если начинается с белой, следом идет черная, следом белая и так далее. Я принял за точку отсчета белую клетку с координатой (1;1).
Всё дальнейшее рассуждение некорректное, но оставлено как есть чтобы передать ход мыcлей.
Следующая белая имела бы координату (1;3), затем (1;5) и последняя в ряду (1;7). Белые второго ряда имели бы координаты (2;2), (2;4), (2;6), (2;8). Следующий третий ряд повторял бы первый ряд и отсюда уже можно было сделать вывод, что белые в нечетных рядах имеют нечетные координаты а в четных четные и наоборот, черные в нечетных рядах имели бы четные координаты а в четных нечетные. Это уже само по себе подсказывает решение, но я в тот момент этого не понял и решил действовать так, буду сравнивать координаты первой и второй клетки шаг за шагом. Чтобы определять нечетные и четные клетки решил воспользоваться остатком от деления на 2. Четные числа имели бы в остатке 0, так как любое четное число делится на два без остатка, отсюда вытекает обратное, что если число делиться на 2 без остатка то оно четное. А нечетные 1. Но и это не пришло мне в голову, логика отдыхала. Поэтому нечетные клетки я обозначил как остаток отделения не равный 0. Координаты первой клетки обозначались переменными (a;b), а второй (c;d). Условие было таким.
Данный код прошел все тесты с различными входными данными и успешно выполнил задание.
Что c ним (с кодом) не так? Да наверное все. Это пример того, как не нужно писать код, именно такое программисты называют говнокод.
Как правильно нужно было решить задачу?
Для этого надо было включить логику и хорошенько подумать. Во первых обозначить координаты правильно (x1;y1), а для второй клетки (x2;y2). Если бы я это сделал сразу то тогда возможно понял бы, что не правильно передаю координаты клетки. Для первого ряда координаты белых будут не (1;1), (1;3) и т.д., а (1;1), (3;1)! и т.д.. Для черных (2;1), (4:1) и т.д.. Для второго ряда для белых (2;2), (4;2), а для черных (1;2), (3;2) и т.д.. Всмотримся в координаты повнимательнее. Сумма координатов белых всегда в любом ряду четная, а для черных нечетная! Т.е. можно наугад взять любой столбец по x, например 7 и раз он нечетный значит в сумме с нечетной строкой по y он даст четное число, т.е. белый цвет. Проверим, (7;1) — белый, (7;5) — белый. А в сумме с четным числом даст нечетное, т.е. черный цвет. (7;2) — черный как и (7;6). Что это нам дает? А это нам дает отличное решение.
Можно поступить еще проще, просто сравнить остатки от деления на 2 сумм координатов первой и второй клетки, если они равны, то соответственно клетки тоже одинаковые, ведь если обе клетки с четными координатами то остатки будут нулями, а если нечетные то единицей:
Если и дальше рассуждать логически можно прийти к следующему. Сумма координатов каждой из клеток может быть либо четной либо нечетной. А сумма двух четных или двух нечетных чисел всегда будет четное число. Отсюда мы можем написать следующее условие. Если сумма координатов обеих клеток четное число то значит и клетки одинаковые.
Это и есть код разработчиков задачи. Цель моего обучения программированию прийти в итоге к вот таким изящным решениям задач и писать не говнокод, а писать качественный код, лаконичный код, чтобы программки были как можно меньше, менее требовательны к ресурсам при том же функционале и за счет этого были быстрые и качественные. Задачки с шахматами продолжатся, теперь уже с фигурами, про них напишу в следующей заметки, так как эта и так получилась очень объемной.
Опубликованно April 13th, 2018 by Aziz Madazimov
Олимпиада по математике школьный этап 2021 ВОШ задания и ответы для 4-11 класса
ПОДЕЛИТЬСЯ
Задания и ответы школьного этапа 2021 олимпиады по математике для 4-11 класса всероссийской олимпиады школьников 2021-2022 учебного года, официальная дата проведения олимпиады в Омске: 06.10.2021 (6 октября 2021 года)
Задания и ответы для 4 класса: скачать
Задания и ответы для 5 класса: скачать
Задания и ответы для 6 класса: скачать
Задания и ответы для 7 класса: скачать
Задания и ответы для 8 класса: скачать
Задания и ответы для 9 класса: скачать
Задания и ответы для 10 класса: скачать
Задания и ответы для 11 класса: скачать
Интересные задания и ответы олимпиады:
1)Ваня представил число 100 в виде суммы 14 слагаемых, имеющих одинаковую сумму цифр: 100=20+20+20+20+2+2+2+2+2+2+2+2+2+2 (сумма цифр числа 20 равна 2+0=2). Вася смог представить число 100 в виде суммы 11 слагаемых, имеющих одинаковую сумму цифр. Как он это сделал? Достаточно привести один пример такого представления.
Ответ: 100=50+5+5+5+5+5+5+5+5+5+5.
2)Вера, накопив 200 рублей, хотела купить пенал, но этих денег ей не хватило. Через несколько дней пенал уценили, и он стал стоить в два раза меньше. Теперь Вера смогла его купить и даже получила сдачу 15 рублей. Сколько стоил пенал первоначально? Ответ нужно подтвердить вычислениями и объяснениями.
Ответ: 370 р.
3)Фермер огородил снаружи участок земли и разделил его на квадратики со стороной 3 м. В пяти квадратиках он разместил гусятники (обозначены «Г»), а в других пяти – будки со сторожевыми собаками (обозначены «С»). Но гуси нападают на собак, а собаки могут загрызть гусей. Помогите фермеру построить по линиям сетки дополнительные заборы общей длины 30 м, чтобы защитить собак от гусей и гусей от собак.
Ответ: например, так, как на рисунке справа.
4)По кругу стоят 10 сорочат. Мама–сорока кормит их кашей: первому – 1 ложку, второму – 2 ложки, следующему – 1, потом – 2 и так далее. Всего она раздала 55 ложек каши, и на этом каша закончилась. Сколько сорочат получили ровно 4 ложки каши? Ответ нужно обосновать.
Ответ: 4 птенца
5)Никита записал два нечётных числа, а потом заменил в них разные цифры разными буквами, а одинаковые – одинаковыми. У Никиты получились два слова: УЧИТЕЛЯ и МЕЧТАТЕЛИ. Известно, что произведение цифр числа УЧИТЕЛЯ не равно нулю, а произведение цифр числа МЕЧТАТЕЛИ равно нулю. Чётной или нечётной будет сумма Я+И+МЕЧТА? Ответ нужно обосновать.
Ответ: чётная
6)В семье Веснушкиных три человека, и у каждого на лице в два раза больше веснушек, чем ему лет. Васе сейчас 11 лет. Васина мама младше Васиного папы на 3 года, и у неё на лице 66 веснушек. Сколько веснушек на лице у всех троих вместе? Ответ нужно подтвердить вычислениями и объяснениями.
Ответ: 160 веснушек.
7)Найдите какое-нибудь решение неравенства М Ответ: например, М=1, А=3, Т=2, Е=4, И=5, К=9, т.е. 1
8)Маша попросила встать 30 одноклассников по кругу и стала раздавать им шоколадные конфеты. Первому дала 1 конфету, второму – 2 конфеты, следующему – снова 1 конфету, потом – 2 конфеты и так далее. Всего она раздала 55 конфет, и на этом конфеты закончилась. Сколько Машиных одноклассников получили ровно 2 конфеты? Ответ нужно обосновать
Ответ: 16 человек
9)На рисунке слева изображена фигура на клетчатой бумаге. Сторона каждой клетки равна 1 см. Разрежьте данную фигуру по линиям сетки на фигурки, удовлетворяющие всем четырём условиям: 1) площадь каждой равна 5 см2 ; 2) периметр каждой равен 12 см; 3) все фигурки должны быть различными, т.е. не совпадать при наложении; 4) в каждой должен быть ровно один серый квадратик. Достаточно привести один вариант разрезания.
Ответ: например, как на рисунке ниже.
10)Винни-Пух, Пончик и Карлсон приняли участие в турнире обжор. По результатам трёх туров судья заполнил таблицу, где указал, сколько пирогов в каждом туре съел каждый участник. Оказалось, что все числа в таблице различны. Ночью каждый из участников увеличил только один из своих результатов в таблице на 1. Утром все увидели следующую таблицу.
Ответ: см. файл выше
11)На клетчатой бумаге нарисован прямоугольник 3х4 клетки. Разрежьте его по сторонам клеток на 3 части так, чтобы из них можно было сложить фигуру, изображенную справа.
Ответ: вариант разрезания приведен: 1-я часть с цифрами «1», 2-я часть – «2» и 3-я часть – «3». Из них легко складывается нужная фигура.
12)Мальвина написала на доске выражение М+А = Т+Е = М+А+Т = И+К+А и попросила Буратино заменить все буквы цифрами так, чтобы равенства оказались верными. Причем разные буквы нужно заменять разными цифрами, а одинаковые буквы ‒ одинаковыми цифрами. Помогите Буратино справиться с задачей. Достаточно привести хотя бы один пример.
Ответ: пусть М=5, А=2, Т=0, Е=7, И=1, К=4. Тогда получим верные равенства: 5+2=0+7=5+2+0=1+4+2.
13)Семи детям раздали 55 конфет. После этого первыйсказал, что по крайней мере 1 конфета у него имеется. «А у меня ровно на две больше!» — сказал второй. «А у меня ровно на две больше, чем у тебя!» — сказал третийвторому, затем такую же фразу произнес четвертый— третьему, пятый – четвертому, шестой— пятому. А седьмой заявил: «А у меня конфет больше всех!». Сколько конфет получил седьмой ребенок? Найдите все варианты и докажите, что других нет.
Ответ: 13 или 19
14)У Алисы есть три деревянных кубика. Длина ребра меньшего кубика равна 1 дм, среднего — 2 дм, большего — 3 дм. На покраску меньшего кубика ей потребовалось на 120 г краски меньше, чем на покраску среднего кубика. Сколько граммов краски ей потребуется на покраску большего кубика?
Ответ: 360 г.
15)Чтобы насытиться, голодному кролику нужно съесть ровно три каких-нибудь различных овоща. Какое наибольшее количество голодных кроликов можно накормить досыта, если в запасах имеется 5 кукуруз, 8 огурцов, 11 морковок и 17 перцев? Ответ нужно обосновать.
Ответ: 12
16)На клетчатой бумаге нарисован прямоугольник 3х4 клетки. Разрежьте его по сторонам клеток на 3 части так, чтобы из них можно было сложить фигуру, изображенную справа.
Ответ: вариант разрезания приведен: 1-я часть с цифрами «1», 2-я часть – «2» и 3-я часть – «3». Из них легко складывается нужная фигура.
17)Замените буквы A, B, C, D, E, F, G, K цифрами от 1 до 8 без повторений так, чтобы числа 6, 11, 16, 21 в серых треугольниках являлись суммами цифр, стоящих в трёх белых треугольниках, соседствующих по сторонам с серым.
Ответ: подходящие значения букв: А=2, В=3, С=5, D=1, Е=8, F=4, G=6, К=7. Легко проверить, что условие задачи выполняется.
18)Рыбак поймал 6 кг рыбы. Часть приготовил себе, остальное отдал трём котам. Каждый кот съедает в 2 раза больше рыбы, чем рыбак за одно и то же время. Сколько килограммов рыбы было отдано котам, если есть все начали одновременно, а коты съели свою часть в 2 раза быстрее, чем рыбак?
Ответ: 4,5 кг.
19)Три одинаковых кубика приставлены друг к другу гранями с одинаковым числом очков. Найдите сумму чисел на трёх нижних гранях кубиков данной конструкции, на верхних гранях которых числа 3, 5 и 6.
Ответ: 7
20)Лиса Алиса, Буратино и Пьеро нашли 110 золотых монет. Алиса предложила разложить их на три кучки и сказала: «Пусть жребий определит, кому какая достанется!» Чтобы мальчики не расстраивались, они договорились уравнять свои кучки по меньшей, а лишнее отдать Алисе. (Например, если Буратино достанется 10 монет, Пьеро – 15, а Алисе – 85 монет, то Пьеро отдаст Алисе 5 монет, чтобы у него с Буратино стало поровну). Алисе необходимо разложить все монеты на три кучки так, чтобы в результате ей наверняка досталось не меньше 100 золотых монет. Сколько у нее есть вариантов?
Ответ: 15
21)Сколько раз в последовательности из 12 чисел: 2, _, _, _, _, _, _, _, _, _, _,1 (на первом месте стоит 2, на последнем месте 1) встретится цифра 2, если известно, что сумма любых трех чисел, идущих подряд, равна 5?
Ответ: 8 раз
22)На турнир «рыцарей и лжецов» математического кружка ребята мастерили из квадратного листа картона размером 150см×150см стену рыцарского замка. По краям и в середине было вырезано три одинаковых квадрата. Петя заметил, что при этом периметр первоначального листа увеличился на 8%. Найдите площадь получившейся «стены».
Ответ: 20772 см2
23)Петя и Вася живут в одном доме и выходят в школу одновременно. Петя сначала считает ворон и идет со скоростью 4 км/ч, но ровно на середине пути на парковке пересаживается на велосипед и едет со скоростью 12 км/ч. Вася идет в школу с постоянной скоростью и приходит в школу одновременно с Петей. Учитель Степан Иванович на середине пути обгоняет Петю на мопеде, так как его скорость в 5 раз больше скорости Васи, он приезжает в щколу на 3 минуты раньше мальчиков. Найдите расстояние от дома мальчиков до школы.
Ответ: 2км
24)По данным, изображенным на рисунке справа, найти длину катета BC прямоугольного треугольника АВС.
Ответ: 12
25)Какое наибольшее число «тетраминошек» (как на рисунке) можно разместить внутри квадрата 6×6 без наложений? Фигурки можно как угодно поворачивать и переворачивать.
Ответ: 8
26)Назовем прямоугольник «симпатичным», если его длинная сторона меньше удвоенной короткой. (В частности, квадрат является симпатичным прямоугольником). Разрежьте квадрат площади 100 на четыре симпатичных прямоугольника с площадями 10, 20, 30 и 40.
28)Винни-Пух заготовил мёд на зиму в нескольких полных горшочках по 5 литров каждый. Если бы он свои запасы мёда разлил в 4-литровые горшочки, то их потребовалось бы на четыре больше, правда, один горшочек оказался бы неполным. А если разлить весь мёд в горшочки по 7 литров, то их потребовалось бы на четыре меньше первоначального количества. Но один горшочек снова оказался бы неполным. Сколько горшочков мёда заготовил Винни-Пух?
29)Из вершин А, В и С треугольника АВС провели соответственно медиану АМ, биссектрису ВK и высоту СH. Оказалось, что середина отрезка ВK совпадает с серединой отрезка MH. Найдите углы треугольника АВС.
30)На каникулах для всех желающих провели турнир по шашкам. Каждый сыграл с каждым ровно одну партию. За победу в партии участник турнира получал 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Известно, что среди участников мальчиков было в десять раз больше, чем девочек, и они вместе набрали в 4,5 раза больше очков, чем девочки. Сколько очков набрала самая успешная девочка?
31)Девятиклассник Дима выписывает ряд последовательных трёхзначных чисел так, чтобы каждое число делилось нацело на свою последнюю цифру. Какое наибольшее количество чисел могло быть в этом ряду?
32)Имеется сталь двух сортов с содержанием никеля 55% и 12%. Сколько нужно взять металла каждого из сортов, чтобы получить 2021 т стали с содержанием 32% никеля?
33)Вася выписывает последовательность из 2021 натуральных чисел, начиная с некоторого числа, так, чтобы сумма любых трех подряд идущих чисел была равна 5. Какое наибольшее количество двоек у него может получиться?
34)На стороне ВС треугольника АВС выбрана точка F. Оказалось, что отрезок AF пересекает медиану BD в точке Е так, что АЕ = ВС. Докажите, что BF = FE.
35)Имеются две бочки с водой бесконечной вместимости и два ковшика объемами 2 и 2 2 литров. Можно ли, пользуясь этими ковшиками, перелить из одной бочки в другую ровно 1 литр?
36)От 2 кусков сплавов с разным содержанием свинца массой 6 кг и 12 кг отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого сплава, после чего процентное содержание свинца в обоих сплавах стало одинаковым. Каковы массы отрезанных кусков?
37)Художник Петров красит плоскость в два цвета произвольным образом, а геометр Васильев утверждает, что сможет построить треугольник с вершинами одного цвета, величины углов которого относятся как 4:2:1. Прав ли он?
Олимпиада по информатике (школьный тур, 7-8 кл)
Выбранный для просмотра документ Задания 7-8.doc
ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ ПО ИНФОРМАТИКЕ. ШКОЛЬНЫЙ ТУР
Задание 1 «Исполнитель Двоечка»
Имеется исполнитель «Двоечка», имеющий следующую последовательность команд:
Удваивает данное число.
Прибавляет к данному числу 2, если данное число четное и вычитает из данного числа 2, если данное число нечетное.
Возвращает целую часть от деления данного числа на 2.
Возвращает остаток от деления данного числа на 2.
Приписывает к данному числу цифру 2 слева.
Приписывает к данному числу цифру 2 справа.
К исходному числу 143 применили следующую последовательность команд: 2352646
Какое число получится в результате?
В трёхзначном числе не меньше двух цифр, которые меньше 6, и не меньше двух чётных цифр. Найдите самое большое из таких чисел.
Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может.
У Робота есть девять команд. Четыре команды – это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится.
Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды – это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
На бесконечном поле имеется горизонтальная стена. Длина стены неизвестна. От правого конца стены вверх отходит вертикальная стена также неизвестной длины. Робот находится в углу между вертикальной и горизонтальной стеной.
Один из возможных способов расположения стен и Робота приведен на рисунке (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные выше горизонтальной стены и левее вертикальной стены и прилегающие к ним. Робот должен закрасить только клетки, удовлетворяющие данному условию.
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стены внутри прямоугольного поля. В результате исполнения алгоритма Робот не должен разрушиться.
Заполните пропуски в предложенном алгоритме, вписав необходимые команды и условия.
Задания 4, 5 на программирование. Вам необходимо составить алгоритм или программу для решения задач.
Задания могут быть выполнены как в компьютерном, так и в безкомпьютерном вариантах.
Если вы работаете без компьютера, то необходимо на отдельном листе записать текст программы и указать используемый язык программирования или записать алгоритм решения задачи любым способом (словесным, табличным, блок-схемой).
Если вы работаете на компьютере, то вы сохраняете программу в папке, которую вам укажет учитель, а в бланк ответов записываете имя файла с программой.
Задание 4 «Чья комната больше»
Напишите программу, которая определит, чья комната больше: Машина или Петина.
Формат входных данных
Формат выходных данных
Если Машина комната больше, выведите латинскую букву «М». Если Петина комната больше, выведите латинскую букву «Р». Если комнаты ребят имеют одинаковую площадь, выведите латинскую букву «Е».
Шахматная доска состоит из n × m клеток, покрашенных в черный и белый цвет в «шахматном» порядке. Клетка в левом нижнем углу доски покрашена в черный цвет. Определите, сколько всего на доске черных клеток.
Формат входных данных
Программа получает на вход два числа n и m, записанных в отдельных строках. Все числа — натуральные, не превосходящие 30 000.
Формат выходных данных
Программа должна вывести одно целое число — количество черных клеток на доске.
Создаем несложный шахматный ИИ: 5 простых этапов
Перевели для вас статью Лори Хартикка (Lauri Hartikka) о создании простейшего ИИ для шахмат. Она написана еще в 2017 году, но базовые принципы остались теми же. Все файлы, которые использовал Лори, тоже доступны.
Простой искусственный интеллект, который умеет играть в шахматы, можно создать на базе четырех концепций:
Напоминаем: для всех читателей «Хабра» — скидка 10 000 рублей при записи на любой курс Skillbox по промокоду «Хабр».
Готовый исходный код можно найти на GitHub.
I’m having trouble beating a chess program I wrote.
Not sure if I’m a bad player or the algorithm is decent.
Этап 1. Визуализация шахматной доски с генерацией ходов
На этом этапе мы будем использовать библиотеки chess.js для генерации ходов и chessboard.js для визуализации доски. Библиотека, которая отвечает за генерацию ходов, позволяет применять все шахматные правила, так что мы можем рассчитывать каждое действие для конкретного расположения фигур.

При клике на картинке она откроется в полном разрешении.
Работа с этими библиотеками позволяет сконцентрироваться на главной задаче — поиске и создании алгоритма, который позволяет найти оптимальный ход. Работу начинаем с написания функции, которая возвращает случайный ход из списка всех возможных.
Несмотря на то, что алгоритм не является идеальным игроком в шахматы, для большинства игроков его уровня этого будет вполне достаточно.

Черные ходят случайным образом. (исходники и игра онлайн)
Этап 2. Оценка позиции
Теперь давайте разберемся, у какой стороны преимущество в том или ином положении. Самый простой путь — подсчитать относительную силу фигур на доске, это можно сделать при помощи таблицы.
Используя функцию оценки, мы получаем возможность создать алгоритм, который выбирает ход с максимальной оценкой.
В принципе, уровень прежний, но алгоритм уже может взять чужую фигуру, когда такая возможность есть.

Черные получили возможность брать белые фигуры. (Исходники и игра здесь).
Этап 3. Дерево поиска с минимакс
После этого мы создаем дерево поиска. Теперь программа может выбрать из него лучший ход. Это делается при помощи минимакс-алгоритма.
Здесь рекурсивное дерево с отображением всех возможных ходов анализируется до заданной глубины. Позиция же оценивается по листьям нашего дерева.
Далее мы возвращаем минимальное или максимальное значение потомка в родительский узел. Все зависит от того, ход какой стороны сейчас просчитывается. Другими словами, результат максимизируется или минимизируется на каждом из уровней.
С минимакс-алгоритмом наш ИИ уже стал понимать базовую тактику шахмат.
Минимакс с глубиной 2 (Исходники и игра здесь)
Стоит отметить, что эффективность минимакс-алгоритма увеличивается с глубиной поиска. За это отвечает следующий этап.
Этап 4. Альфа-бета-отсечения
Это метод оптимизации минимакс-алгоритма, дающий возможность игнорировать некоторые ветви в дереве поиска. А это позволяет увеличить глубину поиска, затрачивая прежний объем ресурсов.
Альфа-бета-отсечение основано на ситуации, когда мы можем остановить оценку определенной ветви, если обнаруживается, что новый ход приведет к худшей ситуации, чем та, которую мы видели при оценке предыдущего.
На результат минимакса оптимизация не влияет, но все начинает работать быстрее.
Этот алгоритм гораздо более эффективен в том случае, если сначала проверить пути, ведущие к хорошим ходам.
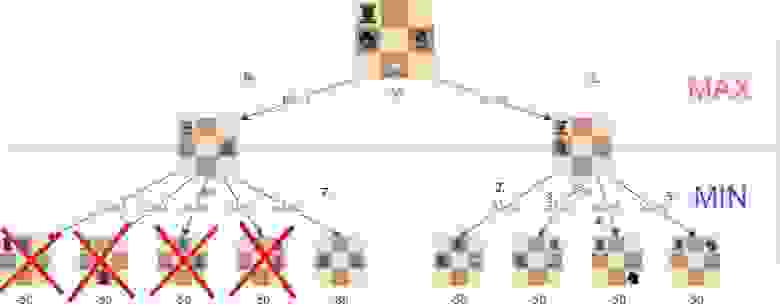
Изображение демонстрирует ходы, которые становятся ненужными в процессе использования альфа-бета-отсечения.
Как видите, с альфа-бета-отсечением минимакс оптимизируется, и весьма значительно.

Количество позиций, которые требуется оценить в случае поиска с глубиной 4 и начальной позицией, которая изображена выше. (исходники и игра доступны здесь)
Этап 5. Улучшенная функция оценки
Изначальная функция оценки достаточно простая, поскольку она просто считает очки фигур, находящихся на доске. Для ее оптимизации можно учитывать положение фигур. К примеру, если разместить коня в центре доски, то он становится дороже — спектр доступных ходов для этой фигуры расширится.
На этом этапе мы будем работать с несколько видоизмененной версией квадратных таблиц, изначально описанной в вики Chess Programming.
И теперь наш алгоритм играет уже весьма неплохо, конечно, по сравнению со средним игроком.

Исходники и игра доступны здесь
Заключение
Достоинством предложенного алгоритма является то, что он не делает совсем уж глупых ошибок. Конечно, стратегию здесь сложно назвать совершенной, но тем не менее.
Реализация нашего алгоритма выполнена всего в 200 строк кода, так что базовые принципы достаточно просты. Финальную версию программы можно github.com/lhartikk/simple-chess-ai’>видеть на GitHub.
В алгоритм можно добавить и другие модули, включая:
Больше о шахматных алгоритмах можно узнать на Chess Programming Wiki.
