оптимизируйте приведенный код реализующий алгоритм пузырьковой сортировки
Как это работает (оптимизация пузырьковой сортировки)?
Всем привет. Изучаю основы Python и в задаче по оптимизации пузырькового алгоритма сортировки столкнулся с тем, что правильный на первый взгляд код выдавал не до конца отсортированный список. Вот сам код:
Методом тыка я выяснил, что в предпоследней строке после ‘else:’ надо оставить только False, а ‘swap =’ убрать. Получилось так:
Всё работает. Но, в чём разница я не понимаю. На 14-м шаге (смотрю на pythontutor) правильный код после строки if a[j] > a[j + 1]: идёт на новый цикл, а не правильный идёт на 12-ю строку и меняет значение переменной swap на False. Собственно вопрос мой следующий: в чём по сути заключается разница между этими двумя вариантами? Мне на первый взгляд казалось, что после else: естественно писать swap = False, ведь мы присваиваем переменной новое значение, значит, она (переменная) должна быть указана слева от знака присвоения, а фактически программа работает только без указания там самой переменной. Понимаю, что упустил что-то важное, но что, не могу додуматься.
Ну так во втором варианте вы убили всю логику связанную со swap т.е. оно никогда не становится false, и соответственно сортирует как и должно до упора.
А когда вы впиливаете туда свой непонятный swap с проверкой, то на следующих итерациях первого цикла ничего не происходит.
Получается что в момент когда сортировка доходит до каких-то двух чисел которые НЕ надо перемещать сортировка ломается об swap = false, а выдаёт то что насортировало до этого момента, а оставшуюся часть в том порядке как было изначально.
Пузырьковая сортировка в Python
Сортировка пузырьком – это простой алгоритм среди различных алгоритмов сортировки. Изучим его как первый алгоритм сортировки. Его легко освоить и он интуитивно очень понятен. Его несложно реализовать в коде, что очень выгодно для начинающих разработчиков программного обеспечения. Минус алгоритма в том, что для сортировки элементов данный метод производит проверку каждый раз, независимо от того, сортируется массив или нет.
Концепция пузырьковой сортировки
Разберемся на примере.
Мы создаем список элементов, в котором хранятся целые числа
list1 = [5, 3, 8, 6, 7, 2]
Так алгоритм сортирует элементы:
Первая итерация
Он сравнивает первые два элемента, и здесь 5> 3, а затем меняет их местами. Теперь у нас есть новый список –
Во втором сравнении 5 6, элементы меняются местами –
В четвертом сравнении 8> 7, элементы меняются местами –
В пятом сравнении 8> 2, также нужно их поменять местами –
На этом первая итерация завершена, и в конце мы получаем самый большой элемент. Теперь нам нужно len (list1) – 1
Вторая итерация
Пятая итерация
Мы видим, что наш список отсортирован с использованием метода пузырьковой сортировки.
Реализация в коде Python
Мы уже описывали технику пузырьковой сортировки. Теперь реализуем логику в коде Python.
В приведенном выше коде мы определили функцию bubble_sort(), которая принимает list1 в качестве аргумента.
Без использования временной переменной
Мы также можем поменять местами элементы, не используя временную переменную. У Python очень уникальный синтаксис. Мы можем использовать следующие строки кода.
Оптимизация реализации кода Python
Мы можем оптимизировать приведенный выше код, используя два метода. Свопы не производятся; это означает, что список отсортирован. В предыдущем методе оценивается полный список, хотя в этом нет необходимости.
Мы можем предотвратить ненужную оценку, используя логический флаг и проверяя, были ли сделаны какие-либо свопы в предыдущем разделе.
Во втором методе мы учитываем тот факт, что итерация заканчивается, когда самый большой элемент списка оказывается в конце списка.
В первый раз мы передаем самый большой элемент в конечную позицию, используя позицию n. Во второй раз мы проходим через позицию n-1, второй по величине элемент.
На каждой последующей итерации мы можем сравнивать на один элемент меньше, чем раньше. Точнее, на k-й итерации нужно сравнить только первые n – k + 1 элементов:
Сравнение времени
Давайте посмотрим на сравнение времени между приведенными выше фрагментами кода.
Все методы применимы для небольшого числа элементов, но если список состоит из многих элементов, то второй метод оптимизации имеет огромное значение.
Оптимизируйте приведенный код реализующий алгоритм пузырьковой сортировки
Оптимизация пузырьковой сортировки. Реализация на C#.
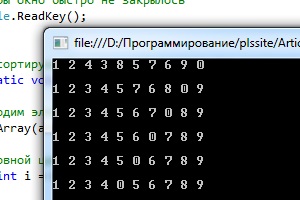
Доброго времени суток! В этой статье я расскажу о простой оптимизации алгоритма пузырьковой сортировки (bubble sort), пример простейшей реализации которого я приводил в предыдущей статье (рекомендую прочесть, чтобы понять суть данной стать). Идея данной оптимизации заключается в сокращении избыточных итераций, т. е. поочередных переборов элементов исходного массива. Работать (давать положительный результат) данная модификация алгоритма будет только в том случае, когда избыточные итерации действительно присутствуют (например, попался почти отсортированный массив). Ниже, приведен результат выполнения программы из предыдущей статьи, с массивом, который практически отсортирован. В консоль выводится массив до сортировки, и после каждого перебора его элементов (и видные перестановки его элементов, выполненные во время каждой из итераций).
Избыточность простой пузырьковой сортировки
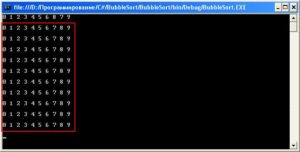
На рисунке отмечены результаты последних итераций, и видно, что массив уже не менялся, так как был отсортирован во время первой итерации (вторая строка в на рисунке), тем не менее, остальные итерации выполнялись (хотя, были явно избыточными), именно про выполнение таких итерация я и говорил в самом начале, точнее, я говорил про исключение таких итераций. А исключаются они очень просто, нужно лишь фиксировать факт перестановки элементов во время каждой итерации. Т. е. если во время поочередного перебора элементов массива была хоть одна перестановка смежных элементов массива местами, то нужно зафиксировать этот факт в переменную типа bool (если были перестановки, переменная будет иметь значение true). А перед каждой последующей итерацией, будет проверяться значение этой самой переменной, если значение будет равно true, то значение переменной будет устанавливаться в false, а итерация запускаться, в противном случае (если значение переменной не равно true) — сортировка прекращается, так как массив уже отсортирован (перестановок во время выполнения предыдущей итерации не было). А вот исходный код, с модифицированным алгоритмом (нововведения, относительно алгоритма, приведенного в предыдущей статье, выделены):
А вот и результат выполнения программы:
Сокращение избыточности простой пузырьковой сортировки
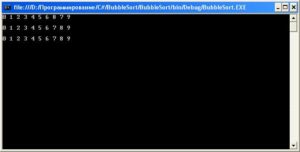
Как видно, количество итераций существенно сократилось (первая строка — вывод исходного массива; вторая — результат первой итерации; третья — результат второй итерации, во время которой и стало понятно, что массив уже отсортирован). Но тем не менее, осталась одна избыточная итерация. Во время неё мы не меняли местами ни какие элементы массива, а значит — и не выполняли полезных действий (т.е. уже не сортировали), а использовали мы эту итерацию, только для того, чтобы понять что массив уже отсортирован. Но если ещё доработать алгоритм, то эта избыточная итерация тоже не понадобится. Ниже я привел исходный код модифицированного алгоритма, вдаваться в подробности я уже не буду (пояснения есть в комментариях), скажу лишь только, что идея данной модификации в подсчете количества перестановок элементов массива в рамках одной итерации:
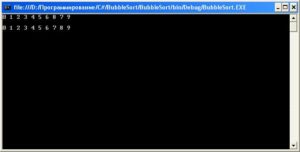
А вот результат (количество итераций сократилось до минимума), первая строка — вывод исходного массива, вторая — результат первой, и единственной необходимой в данном случае итерации:
Сокращение избыточности простой пузырьковой сортировки до минимума
p.s. На самом деле, и эта реализации алгоритма не гарантирует полного отсутствия избыточных итераций, но доведение до совершенства алгоритма пузырьковой сортировки — дело неблагодарное, хотя, можете поэкспериментировать на досуге…
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Сортировка методом пузырька в Python
На сегодняшний день создано множество алгоритмов сортировки, каждый из которых решает весьма распространенную задачу — сортировку данных.
Сортировка пузырьком — это один из самых простых, но и малоэффективных алгоритмов, который используется для сортировки небольших массивов.
Алгоритмы сортировки на собеседовании
Алгоритмов сортировки достаточно много, и вряд ли можно встретить программиста, который может по памяти написать реализацию хотя бы половины из них.
На самом деле, программисты просто гуглят необходимую реализацию. Конечно, они имеют представление о принципах их работы, потому что в своё время рассмотрели несколько алгоритмов, как, например, сортировка пузырьком.
На собеседованиях спрашивают про алгоритмы сортировки, но это не значит, что от будущего работника требуют написать их реализацию или придумать свой. Работодатель требует от специалиста следующее:
Метод пузырька
Сортировка пузырьком в основном применяется в учебных проектах. В реальной практике её заменяют более эффективные алгоритмы, однако сортировка пузырьком лежит в основе некоторых из них.
В общем случае алгоритм сортировки пузырьком следующий:
В алгоритме используется два цикла: основной и вложенный. В результате одного прохода вложенного цикла наибольший элемент помещается в конец массива, а наименьший смещается на одну позицию ближе к началу.
Внешний цикл в худшем случае совершает N (кол-во элементов) — 1 проходов, то есть внутренний цикл выполняется N-1 раз.
Таким образом, в каждом проходе совершается серия обменов элементов так, что наибольший элемент передвигается в конец массив перед элементом, который переместился туда в прошлой итерации. Процесс происходит до тех пор, пока массив не будет отсортирован.
Сложность алгоритма
Сложность алгоритма позволяет дать ему оценку по времени выполнения, то есть определяет его эффективность. Можно выражать сложность по-разному, но чаще всего используется асимптотическая сложность, которая определяет его эффективность при стремлении входных данных к бесконечности.
Точное время выполнения алгоритма не рассматривается, потому что оно зависит слишком от многих факторов: мощность процессора, тип данных массива, используемый язык программирования.
Следует понимать, что с помощью асимптотической функции нельзя точно вычислить время работы алгоритма. Например, дана последовательность «6 5 4 3 2 1», для её сортировки придется сделать максимальное количество проходов. Такой случай называют наихудшим. Если дана последовательность «3 1 2 4 5», то количество проходов будет минимально, соответственно сортировка пройдет гораздо быстрее. Если же дан уже отсортированный массив, то алгоритму сортировки и вовсе не нужно совершать проходов. Это называется наилучшим случаем.
Реализация на Python
Сортировку пузырьком лучше вывести в отдельную функцию. Код функции будет выглядеть так:
Реализовать обмен значений соседних элементов можно в одну строку, использовав множественное присваивание, тогда код будет выглядеть так:
Множественное присваивание — одна из полезных фич Python, позволяющее не вводить дополнительную переменную для обмена значений двух и более переменных.
Чтобы продемонстрировать работу функции пузырьковой сортировки, создадим список, которые необходимо отсортировать:
Отсортируем его с помощью нашей функции и выведем на экран:
Заключение
Метод пузырька гораздо менее эффективен других алгоритмов, однако он имеет простую и понятную реализацию, поэтому часто используется в учебных целях. Кроме того, пузырьковая сортировка может использоваться для работы с небольшими массивами данных.
Знания особенностей алгоритмов сортировки, их сложности и принципов реализации в общем виде пригодятся каждому программисту, желающему пройти собеседование и стать Python-разработчиком.
Русские Блоги
Как Python оптимизирует пузырьковую сортировку
Публичный аккаунт WeChat: отличная трата
Если у вас есть какие-либо вопросы или предложения, оставьте сообщение в фоновом режиме, и я сделаю все возможное, чтобы решить вашу проблему.
Что такое пузырьковая сортировка?
Сначала перейдите к движущемуся изображению, а затем объедините код, чтобы представить процесс выполнения алгоритма сортировки пузырьков.
Базовое издание
Из изображения gif в сочетании с кодом видно, что даже если упорядочены некоторые элементы в текущей последовательности (последние два элемента 4 и 5 последовательности сравнивать не следует), обход элементов все равно будет выполнен, но эта операция Бессмысленно. Это, очевидно, приводит к неэффективности и потреблению ресурсов. В этом случае временная сложность алгоритма сортировки пузырьков составляет O (N ^ 2)
Ввиду низкой эффективности базовой версии пузырьковой сортировки появилась улучшенная версия.
Улучшенная версия
В базовой версии известно, что даже если упорядочены некоторые элементы в текущей последовательности (например, последние 4, 5), обход элемента все равно будет выполнен. И наша улучшенная версия должна решить эту проблему.
Бит флага isSorted добавляется в приведенный выше код с использованием логической переменной isSorted в качестве маркера. Если элементы заменяются в этом раунде сортировки, это означает, что последовательность не в порядке, если нет обмена элементами, это означает, что последовательность уже в порядке и непосредственно выпрыгивает из большого цикла.
Наконец, если вы заинтересованы в Python и Java, нажмите и удерживайте QR-код, чтобы перейти к моей общедоступной учетной записи. Я постараюсь принести вам пользу. Мне не нужно это ценить, у меня нет возможности, я достоин этого. Просто игнорируйте это, если вы не помогаете.