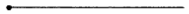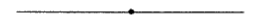Основная и самая простая геометрическая фигура называется

Основная и самая простая геометрическая фигура называется

Точка и прямая являются основными геометрическими фигурами на плоскости.

Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей».

Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол.

Точка является основой для построения любой геометрической фигуры. Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др.

Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямую можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:

Если на прямой вы поставили точку, то этой точкой прямая разбивается па два луча, противоположно направленных. Такие лучи называются дополнительными.

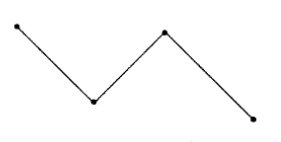
— это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.

Это трехзвенная ломаная линия.

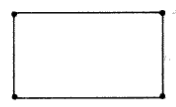
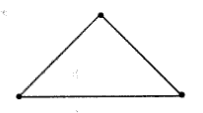
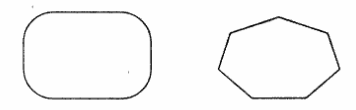
Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник:

Четырехзвенная замкнутая ломаная линия — четырехугольник

Трехзвенная замкнутая ломаная линия — треугольник

, как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.

Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную
геометрическую фигуру:

Источник

Геометрические фигуры. Основные геометрические фигуры.

Основными геометрическими фигурами на плоскости являются точка и прямая линия. Отрезок, луч, ломаная линия — самые простые геометрические фигуры на плоскости.

Точка — мельчайшая геометрическая фигура, являющаяся основой других фигур во всяком изображении либо чертеже.

Каждая более сложная геометрическая фигура есть множество точек, которые обладают определенным свойством, характерное только для этой фигуры.

Прямая линия, либо прямая – это бесконечное множество точек, расположенных на 1-ой линии, которая не имеет начала и конца. На листе бумаги можно увидеть лишь часть прямой линии, т.к. она не имеет предела.

Прямую изображают так:

Часть прямой линии, которая ограничена с 2-х сторон точками, называют отрезком прямой, либо отрезком. Его изображают так:

Луч — это направленная полупрямая, имеющая точку начала и у которой нет конца. Луч изображают так:

Если на прямой поставить точку, то эта точка будет разбивать прямую на 2 противоположно направленных луча. Эти лучи называют дополнительными.

Ломаная линия — несколько отрезков, которые соединены друг с другом таким образом, что конец 1-го отрезка оказывается началом 2-го отрезка, а конец 2-го отрезка — началом 3-го отрезка и так далее, причем соседние (которые имеют 1-ну общую точку) отрезки располагаются на разных прямых. Когда конец последнего отрезка не совпадает с началом 1-го, значит, эта ломаная линия будет называться незамкнутой:

Четырехзвенная замкнутая ломаная линия — четырехугольник (прямоугольник):

Трехзвенная замкнутая ломаная линия — треугольник:

Плоскость, как и прямая, — это исходное понятие, у которого нет определения. У плоскости, как и у прямой, не возможно увидеть ни начала, ни конца. Всегда рассматривается лишь часть плоскости, ограниченная замкнутой ломаной линией.

Источник

Геометрические фигуры. Основные геометрические фигуры.

Основными геометрическими фигурами на плоскости являются точка и прямая линия. Отрезок, луч, ломаная линия — самые простые геометрические фигуры на плоскости.

Точка — мельчайшая геометрическая фигура, являющаяся основой других фигур во всяком изображении либо чертеже.

Каждая более сложная геометрическая фигура есть множество точек, которые обладают определенным свойством, характерное только для этой фигуры.

Прямая линия, либо прямая – это бесконечное множество точек, расположенных на 1-ой линии, которая не имеет начала и конца. На листе бумаги можно увидеть лишь часть прямой линии, т.к. она не имеет предела.

Прямую изображают так:

Часть прямой линии, которая ограничена с 2-х сторон точками, называют отрезком прямой, либо отрезком. Его изображают так:

Луч — это направленная полупрямая, имеющая точку начала и у которой нет конца. Луч изображают так:

Если на прямой поставить точку, то эта точка будет разбивать прямую на 2 противоположно направленных луча. Эти лучи называют дополнительными.

Ломаная линия — несколько отрезков, которые соединены друг с другом таким образом, что конец 1-го отрезка оказывается началом 2-го отрезка, а конец 2-го отрезка — началом 3-го отрезка и так далее, причем соседние (которые имеют 1-ну общую точку) отрезки располагаются на разных прямых. Когда конец последнего отрезка не совпадает с началом 1-го, значит, эта ломаная линия будет называться незамкнутой:

Четырехзвенная замкнутая ломаная линия — четырехугольник (прямоугольник):

Трехзвенная замкнутая ломаная линия — треугольник:

Плоскость, как и прямая, — это исходное понятие, у которого нет определения. У плоскости, как и у прямой, не возможно увидеть ни начала, ни конца. Всегда рассматривается лишь часть плоскости, ограниченная замкнутой ломаной линией.

Источник

Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это это часть плоскости, которая лежит внутри окружности.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник

Геометрические фигуры, изучаемые в школе

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Обращаем Ваше внимание, что c 1 сентября 2022 года вступают в силу новые федеральные государственные стандарты (ФГОС) начального общего образования (НОО) №286 и основного общего образования (ООО) №287. Теперь требования к преподаванию каждого предмета сформулированы предельно четко: прописано, каких конкретных результатов должны достичь ученики. Упор делается на практические навыки и их применение в жизни.

Мы подготовили 2 курса по обновлённым ФГОС, которые помогут Вам разобраться во всех тонкостях и успешно применять их в работе. Только до 30 июня Вы можете пройти дистанционное обучение со скидкой 40% и получить удостоверение.

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Государственное бюджетное профессиональное образовательное учреждение

«Волгодонский педагогический колледж»

Тема: «Геометрические фигуры, изучаемые в начальной школе»

Выполнила: студентка группы ПНК-2

Проверила: Пасечник Г.Н.

2. Геометрические понятия и фигуры, изучаемые в начальной школе(стр.4)

В программе традиционной начальной школы геометрический материал является составной частью курса математики. Он не выделяется в самостоятельный раздел, а включается в программу каждого года обучения.

Одной из основных задач изучения геометрического содержания в курсе математики начальной школы является развитие пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать. Второй важной задачей является формирование у ребенка практических умений измерения и построения геометрических фигур с помощью циркуля, угольника и линейки.

Обязательный минимум содержания образования по математике содержит следующий перечень понятий геометрического характера:

§ Линии: прямые, кривые.

§ Многоугольники: треугольник, прямоугольник, квадрат.

§ Вершины и стороны многоугольника.

§ Вычисление площади прямоугольника.

Геометрические понятия и фигуры, изучаемые в начальной школе

Точка — это основная и самая простая геометрическая фигура.

В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.

Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.

Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.

o Через две точки можно провести единственную прямую.

o Две прямые могут пересекаться только в одной точке.

o Через одну точку можно провести бесконечное множество прямых.

Способы обозначения прямых

Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки. У луча есть начало, но нет конца.

Способы обозначения лучей

Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка). У отрезка есть и начало, и конец.

Основное свойство отрезка — это его длина.

Длина отрезка — это расстояние между его концами.

В математике отрезок обозначается заглавными латинскими буквами.

Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.

Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.

Звенья ломаной — это отрезки ломаной.

В математике ломаная обозначается заглавными латинскими буквами.

Ломаная ABCD.
Вершины ломаной — A, B, C, D.
Звенья ломаной — AB, BC, CD.

Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.

Вершина угла — это точка, в которой два луча берут начало.

Стороны угла — это лучи, которые образуют угол.

Вершина угла — точка O.
Стороны угла — OA и OB.

Для обозначения угла в тексте используется символ:

AOB

Способы обозначения углов

· Одной заглавной латинской буквой, указывающей его вершину.

Угол: O

· Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Угол: AOD

Называть угол можно с любого края, но НЕ с вершины.

Угол с рисунка имеет два названия: AOD и DOA.

· Двумя строчными латинскими буквами.

Угол: fn

Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.

Для обозначения градусов в тексте используется символ: °

50 градусов обозначаются так: 50°

Прямоугольник — это фигура, которая имеет четыре стороны и четыре прямых угла.

У прямоугольника противоположные стороны равны.

В геометрии прямоугольник обозначают четырьмя заглавными латинскими буквами.

Противоположные стороны прямоугольника ABCD: AB = CD, BC = DA.

Квадрат — это прямоугольник, у которого все стороны равны.

В геометрии квадрат, также как и прямоугольник, обозначают четырьмя большими латинскими буквами.

Стороны квадрата KLFM: KL = LF = FM = MK.

Треугольник — это геометрическая фигура, которая имеет три стороны и три угла (вершины треугольника).

Треугольник обозначается тремя заглавными латинскими буквами, перед которыми ставится знак: .

Источник