перевести двоичный код в двоично десятичный код
Двоично-десятичное кодирование
Калькулятор преобразует число из десятичное в двоичное, но записанное упакованным двоично-десятичным кодом, и наоборот.
После калькулятора Перевод дробных чисел из одной системы счисления в другую я думал, что тема с системами счисления уже закрыта. Но, как оказалось, еще нет.
Как я писал по ссылке выше, основная проблема при переводе дробных чисел из одной системы счисления в другую это потеря точности, когда, например, десятичное число 0.8 нельзя перевести в двоичное без погрешности.
Поскольку десятичные числа активно используются человеком, а двоичные — компьютером, этой проблемой в применении к двоичной и десятичной системам однажды уже озаботились какие-то светлые умы и придумали двоично-десятичное кодирование (binary coded decimal, BCD). Суть идеи проста — берем и для каждой десятичной цифры заводим байт. И в этом байте тупо пишем значение десятичной цифры в двоичном коде. Тогда число, например, 0.8 будет 0.00001000. Потом, правда, подумали еще, и решили, что раз уж верхняя часть байта всегда пустует (так как максимум 9 — это 1001), то давайте для каждой десятичной цифры заводить полубайт. И назвали это упакованным двоично-десятичным кодированием (packed BCD).
В упакованном кодировании наше 0.8 будет 0.1000, а какое-нибудь 6.75 будет 0110.01110101.
Прекрасная идея, конечно. Точность не теряется, человек может двоичные числа переводить в десятичные и наоборот прямо на лету, округлять можно, откидывая лишнее. Но как-то не получила она широкого распространения, потому как жизнь машинам она, наоборот, усложняла — и памяти для хранения чисел надо больше, и операции над числами реализовать сложнее. Так и осталась забавным курьезом, и я бы ничего о ней не знал, если бы пользователи не подсказали, что есть такая.
Ну и небольшой калькулятор по этому поводу — вводим либо десятичное число, либо двоичное, подразумевая, что это упакованный двоично-десятичный код, и получаем результат. Понятно, что все преобразования можно проделать и в уме, и в этом ее преимущество; но зачем же лишний раз мозги напрягать, верно?
Welcome to our unique collection of free file converters. More than 10 years of experience make our apps some of the best tools to convert files online. No matter if you want to convert PDFs, Videos, Images or MP3s, you found the right place to go ahead. And we are sure you will be surprised about the quality and performance of our apps. The usage of these converter tools is 100% free, no hidden charges, no sign-up required. We also try not to limit the number of files you can submit or their file size (within the limits of common sense) since we believe it is important to give you the best experience possible. This collection is steadily growing and if you miss a converter here feel free to contact us. We also cover other fields like currency or unit conversion. Not yet convinced? Here is what our clients say:
Converter App overall conversion quality rating





Still looking for the place to convert between different audio, video or document file formats, scientific units or currencies?
We believe you just found it and its free. Select a converter and start converting right now!
Terms and Conditions
All services offered on this site are available for free in the hope that they are useful. We do not give warranty of any kind. Using our converters, you agree to upload your document to a remote server temporarily.
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000 и 9=1001. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).
Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например: 369110=0011 0110 1001 0001DEC:
Десятичное число 3 6 9 1 Двоично-десятичное число 0011 0110 1001 0001
Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Получим 1000 0000 0111 0010DEC = 807210:
Двоично-десятичное число 1000 0000 0111 0010 Десятичное число 8 0 7 2
Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Преобразование двоичных чисел в двоично-десятичные
Арифметико-логическое устройство AVR-микроконтроллеров (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде (в формате целых чисел или чисел с плавающей точкой) удобно выполнять обработку результатов измерения. Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком.
В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные.
1. Форматы представления десятичных чисел
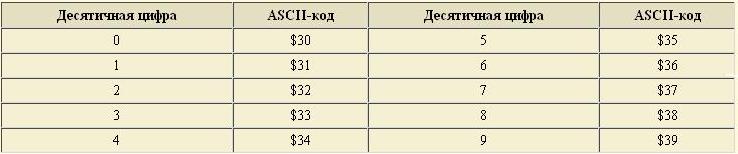
Неупакованный десятичный код является подмножеством международной таблицы кодирования символов ASCII (Таблица 1). Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом. Таблица 1: ASCII-коды десятичных цифр
2. Преобразование целых 16-битных чисел в двоично-десятичные числа
На сайте www.atmel.com предлагается программа «bin2bcd16» для преобразования целых 16-битных двоичных чисел в двоично-десятичные упакованные числа. В данной статье рассматривается программа «bin16bcd5» (см. Приложение, Программа 1), написанная Терешкиным А. В. согласно алгоритму, изложенному в [1], и выполняющая ту же задачу. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая.
Алгоритм программы «bin16bcd5» заключается в следующем. Предположим, что имеется целое беззнаковое 16-битное число (диапазон от 0 до 65535). Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число 10000, сначала определить десятичную цифру десятков тысяч. Затем находится цифра тысяч последовательным вычитанием числа 1000 и т. д. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Программа «bin16ASCII5» (см. Приложение, Программа 2) преобразует целое двоичное 16-битное число в десятичное неупакованное число. При этом используется тот же алгоритм.
3. Преобразование двоичной дроби в двоично-десятичную дробь
Двоичная дробь, по определению, представляется следующим выражением:
Из этого представления следует алгоритм преобразования (Рис. 2), который содержит m шагов. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2.
На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата. Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.
Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.
При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется. При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.
4. Преобразование чисел с плавающей точкой в двоично-десятичные числа
Представление чисел с плавающей точкой имеет следующий вид:
Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел. Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных (а не десятичных) разрядов, на которое необходимо переместить эту точку влево или вправо.
Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля. Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти.
Преобразование двоичного кода в двоично-десятичный
При преобразовании четырехразрядного двоичного числа в двоично-десятичное: числа до 9 включительно остаются без изменения.
Числа свыше 9, представляющие собой псевдотетрады, подвергаются коррекции.
Двоичные числа, содержащие более 4 разрядов, можно преобразовать
аналогичным образом. Для этого двоичное число, начиная со старшего разряда, «вдвигается» справа налево в двоично-десятичную разрядную сетку, как показано на рис. 6. Когда какая-либо единица пересекает границу между двоично-десятичными разрядами, возникает ошибка. Действительно, в случае двоичного числа разрядное значение этой единицы при сдвиге увеличивается с 8 до 16, тогда как для двоично-десятичного числа оно возрастает от 8 до 10. Поэтому на этом этапе двоично-десятичное число как бы уменьшается на 6. Следовательно, для коррекции необходимо прибавлять 6 к числу во всех случаях, когда единица пересекает границу между двоично-десятичными разрядами. К числу десятков надо прибавить 6, если единица перейдет в разряд сотен, и т.д.
Составленное таким образом двоично-десятичное число имеет правильное значение, однако оно может еще содержать псевдотетрады. Чтобы этого не было, возникающие псевдотетрады корректируют непосредственно после каждого шага сдвига, прибавляя 6 к соответствующей декаде с переносом 1 в следующую.
Рис. 6. Преобразование двоичного кода в двоично-десятичный,
в качестве примера взято число 218.
Вместо того чтобы прибавлять после сдвига 6, с тем же успехом можно перед сдвигом прибавлять 3. Необходимость такой коррекции можно также определить перед сдвигом. Если значение тетрады меньше или равно 4 =- 01002, то при последующем сдвиге не произойдет перехода единицы через границу между декадами и не возникнут псевдотетрады. Таким образом, такую тетраду можно будет без изменений сдвигать влево. Если значение тетрады перед сдвигом равно 5, 6 или 7, то также не произойдет перехода единицы через границу, поскольку старший разряд равен нулю. Однако при этом возникнут псевдотетрады: десять, двенадцать, четырнадцать или одиннадцать, тринадцать, пятнадцать (в зависимости от того, будет ли в младший разряд сдвинут нуль или единица). Следовательно, в этих случаях необходима коррекция псевдотетрад путем прибавления 3 перед сдвигом.
Если значение тетрады составляет 8 или 9, необходимо корректировать переход единицы через границу между декадами. Поэтому после каждого сдвига появляются правильные тетрады 6 или 7 либо 8 или 9. При такой коррекции псевдотетрад полученное значение каждой тетрады не может быть более 9. Этим исчерпываются все возможности, и мы получим таблицу коррекции 2.
Преобразование двоичного числа в соответствующее двоично-десятичное можно реализовать, сдвигая влево двоичное число, записанное в регистре сдвига, разделенном на четырехразрядные секции. Каждая секция должна включать корректирующий элемент, который преобразует содержание регистра перед каждым последующим сдвигом в соответствии с таблицей переключений 3.
Наряду с подобным способом реализации преобразования кодов с помощью схем с памятью можно использовать комбинационные схемы, в которых операция сдвига проводится с помощью соответствующей логики. Эта схема представлена на рис. 7. Вместо сдвига числа справа налево здесь слева направо
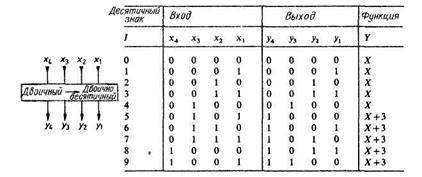
Таблица 2.Таблица переключений корректирующею элемента
для преобразования двоичною кода в двоично-десятичный
«сдвигателя» границы двоично-десятичных разрядов, а каждая полученная тетрада корректируется в соответствии с табл. 2. Следовательно, для «сдвига» разрядной сетки с помощью комбинационной схемы на каждую декаду и каждый шаг сдвига необходимо по одному корректирующему элементу. Эта схема несколько упрощается, если исключить те корректирующие элементы, ко входам которых подключено менее трех двоичных разрядов, поскольку
в этом случае коррекция не нужна. На рис. 7 приведена комбинационная схема для преобразования 8-разрядного двоичного числа. Эту схему легко распространить на любое число разрядов. Элементы, не используемые для преобразования 8-разрядного числа, показаны пунктиром. С помощью записанных здесь чисел можно проследить за процессом преобразования кода для примера, приведенного
Корректирующие комбинационные схемы поставляются в виде программируемых изготовителем микросхем ПЗУ емкостью 32 байта. В одном корпусе размещаются три корректирующих элемента (рис. 8). Так как, согласно рис. 7, младший разряд не подается на корректирующую схему, то с помощью одной ИС можно преобразовать 6-разрядное двоичное число, а для 8-разрядного числа нужны три таких ИС.
Преобразование двоичного кода в двоично-десятичный.
При преобразовании четырехразрядного двоичного числа в двоично-десятичное: числа до 9 включительно остаются без изменения.
Числа свыше 9, представляющие собой псевдотетрады, подвергаются коррекции.
Двоичные числа, содержащие более 4 разрядов, можно преобразовать
аналогичным образом. Для этого двоичное число, начиная со старшего разряда, «вдвигается» справа налево в двоично-десятичную разрядную сетку, как показано на рис. 6. Когда какая-либо единица пересекает границу между двоично-десятичными разрядами, возникает ошибка. Действительно, в случае двоичного числа разрядное значение этой единицы при сдвиге увеличивается с 8 до 16, тогда как для двоично-десятичного числа оно возрастает от 8 до 10. Поэтому на этом этапе двоично-десятичное число как бы уменьшается на 6. Следовательно, для коррекции необходимо прибавлять 6 к числу во всех случаях, когда единица пересекает границу между двоично-десятичными разрядами. К числу десятков надо прибавить 6, если единица перейдет в разряд сотен, и т.д.
Составленное таким образом двоично-десятичное число имеет правильное значение, однако оно может еще содержать псевдотетрады. Чтобы этого не было, возникающие псевдотетрады корректируют непосредственно после каждого шага сдвига, прибавляя 6 к соответствующей декаде с переносом 1 в следующую.
Рис. 6. Преобразование двоичного кода в двоично-десятичный,
в качестве примера взято число 218.
Вместо того чтобы прибавлять после сдвига 6, с тем же успехом можно перед сдвигом прибавлять 3. Необходимость такой коррекции можно также определить перед сдвигом. Если значение тетрады меньше или равно 4 =- 01002, то при последующем сдвиге не произойдет перехода единицы через границу между декадами и не возникнут псевдотетрады. Таким образом, такую тетраду можно будет без изменений сдвигать влево. Если значение тетрады перед сдвигом равно 5, 6 или 7, то также не произойдет перехода единицы через границу, поскольку старший разряд равен нулю. Однако при этом возникнут псевдотетрады: десять, двенадцать, четырнадцать или одиннадцать, тринадцать, пятнадцать (в зависимости от того, будет ли в младший разряд сдвинут нуль или единица). Следовательно, в этих случаях необходима коррекция псевдотетрад путем прибавления 3 перед сдвигом.
Если значение тетрады составляет 8 или 9, необходимо корректировать переход единицы через границу между декадами. Поэтому после каждого сдвига появляются правильные тетрады 6 или 7 либо 8 или 9. При такой коррекции псевдотетрад полученное значение каждой тетрады не может быть более 9. Этим исчерпываются все возможности, и мы получим таблицу коррекции 2.
Преобразование двоичного числа в соответствующее двоично-десятичное можно реализовать, сдвигая влево двоичное число, записанное в регистре сдвига, разделенном на четырехразрядные секции. Каждая секция должна включать корректирующий элемент, который преобразует содержание регистра перед каждым последующим сдвигом в соответствии с таблицей переключений 3.
Наряду с подобным способом реализации преобразования кодов с помощью схем с памятью можно использовать комбинационные схемы, в которых операция сдвига проводится с помощью соответствующей логики. Эта схема представлена на рис. 7. Вместо сдвига числа справа налево здесь слева направо
Таблица 2.Таблица переключений корректирующею элемента
для преобразования двоичною кода в двоично-десятичный
«сдвигателя» границы двоично-десятичных разрядов, а каждая полученная тетрада корректируется в соответствии с табл. 2. Следовательно, для «сдвига» разрядной сетки с помощью комбинационной схемы на каждую декаду и каждый шаг сдвига необходимо по одному корректирующему элементу. Эта схема несколько упрощается, если исключить те корректирующие элементы, ко входам которых подключено менее трех двоичных разрядов, поскольку
в этом случае коррекция не нужна. На рис. 7 приведена комбинационная схема для преобразования 8-разрядного двоичного числа. Эту схему легко распространить на любое число разрядов. Элементы, не используемые для преобразования 8-разрядного числа, показаны пунктиром. С помощью записанных здесь чисел можно проследить за процессом преобразования кода для примера, приведенного
Корректирующие комбинационные схемы поставляются в виде программируемых изготовителем микросхем ПЗУ емкостью 32 байта. В одном корпусе размещаются три корректирующих элемента (рис. 8). Так как, согласно рис. 7, младший разряд не подается на корректирующую схему, то с помощью одной ИС можно преобразовать 6-разрядное двоичное число, а для 8-разрядного числа нужны три таких ИС.
Дата добавления: 2015-12-08 ; просмотров: 2599 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ