Площади подобных трапеций abcd и a1b1c1d1 относятся как 1 25 чему

12.09.202212.09.2022 admin 0 Comments

Площади подобных трапеций abcd и a1b1c1d1 относятся как 1 25 чему

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

`d_1^2+d_2^2=c_1^2+c_2^2+2ab`.

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

Источник

Произвольная трапеция

Свойства трапеции:

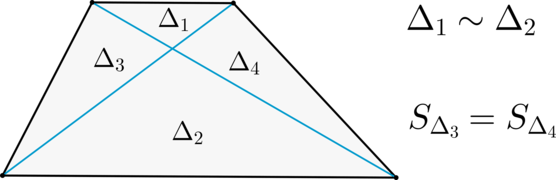
$\blacktriangleright$ Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.

$\blacktriangleright$ Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основаниям и равна их полусумме.

Площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

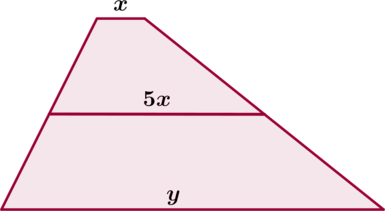
Одно из оснований трапеции в $5$ раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?

В трапеции $ABCD$ средняя линия составляет $\dfrac<4><5>$ одного из оснований. Найдите отношение длины другого основания к длине средней линии.

Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.

Как подготовиться к экзамену?

Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.

Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или «Равнобедренная трапеция», который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».

«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.

Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Источник

Площади подобных трапеций abcd и a1b1c1d1 относятся как 1 25 чему

В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания равна 20, а боковое ребро AA₁ = 7. Точка M принадлежит ребру A₁D₁ и делит его в отношении 2 : 3, считая от вершины D₁.

а) Докажите, что сечение этой призмы плоскостью, проходящей через точки B, D и M, является равнобедренной трапецией.

б) Найдите площадь этой трапеции.

а) Отрезок параллелен диагонали (точка принадлежит ребру ), следовательно, искомое сечение — трапеция (рис. 1). Плоскость сечения пересекает нижнее основание no прямой параллельной значит, параллелен

Треугольники и подобны, следовательно, Значит,

В равных прямоугольных треугольниках и значит, трапеция равнобедренная.

б) Пусть — высота трапеции проведённая к основанию (рис. 2), тогда:

Ответ:

В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания равна 11, а боковое ребро AA₁ = 7. Точка K принадлежит ребру B₁C₁ и делит его в отношении 8 : 3, считая от вершины B₁.

а) Докажите, что сечение этой призмы плоскостью, проходящей через точки B, D и K, есть равнобедренная трапеция.

б) Найдите площадь этого сечения.

а) Пусть — точка, в которой плоскость сечения пересекает ребро Так как плоскости и параллельны, то плоскость сечения пересекает их по параллельным прямым, следовательно, отрезок параллелен диагонали Искомое сечение — трапеция (рис. 1). Плоскость сечения пересекает нижнее основание по прямой параллельной значит, параллельно

Значит,

В равных прямоугольных треугольниках и имеем значит, трапеция равнобедренная.

б) Пусть — высота трапеции проведённая к основанию (рис. 2), тогда:

Ответ :

Аналоги к заданию № 501710: 502294 511377 Все

Дана трапеция ABCD с основаниями AD и ВС. Диагонали АС и BD пересекаются в точке О, а прямые АВ и CD — в точке К. Прямая КО пересекает стороны ВС и AD в точках М и N соответственно, и угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность.

а) Докажите, что треугольник AKD тупоугольный.

б) Найти отношение площадей треугольника ВКС и трапеции ABCD.

а) Как известно, точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой, поэтому и — середины и соответственно. Из условий описанности находим откуда Значит, и

б) Опустим высоту на Пусть тогда

Итак, поэтому треугольники и подобны с коэффициентом

Значит,

Ответ: б)

В основании прямой призмы ABCDA₁B₁C₁D₁ лежит квадрат ABCD со стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD₁, причём BE = 1.

б) Найдите угол между плоскостью сечения и плоскостью ABC.

а) Рассмотрим сечение призмы плоскостью ABC₁D₁. Точка Е лежит в этой плоскости вместе с прямой BD₁. Следовательно, прямые и также лежат в этой плоскости. Пусть они пересекаются в точке M, таким образом, точка M также лежит в искомом сечении. Аналогично, и лежат в сечении BCA₁D₁ и пересекаются в точке Трапеция — искомое сечение.

б) а Поэтому Из подобия треугольников D₁C₁E и BME находим, что откуда BM = MA = 1. Аналогично, BN=1, треугольник BMN — равнобедренный. Опустим перпендикуляр на прямую По теореме о трёх перпендикулярах и, значит, — искомый угол.

Из треугольника AHM, подобного BMN, находим, что Тогда

Ответ: б)

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Треугольники и равнобедренные, так как и Следовательно, средняя линия равна

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 46. Найдите ее среднюю линию.

Треугольники CFO и BEO — равнобедренные, так как и следовательно, средняя линия равна

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 9. Найдите ее среднюю линию.

Треугольники и – равнобедренные, так как и следовательно, средняя линия равна

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 18. Найдите ее среднюю линию.

Треугольники и — равнобедренные, так как и следовательно, средняя линия равна

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 48. Найдите ее среднюю линию.

Треугольники и — равнобедренные, так как и следовательно, средняя линия равна

Найдите площадь ромба, если его диагонали равны 4 и 12.

Площадь ромба равна половине произведения его диагоналей. Поэтому

Найдите площадь ромба, если его диагонали равны 4 и 12.

Площадь ромба равна половине произведения его диагоналей. Поэтому

Найдите площадь ромба, если его диагонали равны 4 и 38.

Площадь ромба равна половине произведения его диагоналей. Поэтому

Найдите площадь ромба, если его диагонали равны 15 и 6.

Площадь ромба равна половине произведения его диагоналей. Поэтому

В правильной четырёхугольной призме АВСDА₁В₁С₁D₁ сторона АВ основания равна 6, а боковое ребро АА₁ равно На ребрах BC и C₁D₁ отмечены точки К и L соответственно, причём ВК = 4, C₁L = 5. Плоскость γ параллельна прямой BD и содержит точки К и L.

а) Докажите, что прямая AC₁ перпендикулярна плоскости γ.

б) Найдите расстояние от точки B₁ до плоскости γ.

а) Так как плоскость параллельна диагонали основания BD, то пересекает основание ABCD по прямой KK₁ параллельной BD, K₁ лежит на CD. Так как, прямая сечения LL₁ параллельна BD, где L₁ лежит на B₁C₁. Сечением призмы будет трапеция

Для того, чтобы прямая была перпендикулярна плоскости, необходимо, чтобы она была перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Заметим, что проекцией прямой AC₁ на плоскость ABCD является прямая AC. Кроме того, как диагонали квадрата таким образом по теореме о трех перпендикулярах следовательно,

Рассмотрим плоскость AA₁C₁C. Пусть эта плоскость пересекает прямые KK₁ и LL₁ в точках E и F соответственно. O — точка пересечения EF и AC₁. Четырёхугольник AA₁C₁C — прямоугольник, причём

Так как AA₁C₁C прямоугольник, Значит, Таким образом,

Тогда по обратной теореме Пифагора следовательно, треугольник прямоугольный, Таким образом,

б) Расстояние от точки B₁ до плоскости равно расстоянию до нее от любой точки параллельной ей прямой B₁D₁. Из точки M — пересечения диагоналей грани в плоскости AA₁C₁C опустим перпендикуляр MH на прямую EF. Так как, по доказанному в п. а) плоскость следовательно, указанный перпендикуляр — искомое расстояние. Найдем Заметим, Таким образом,