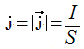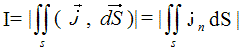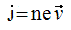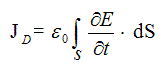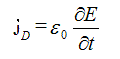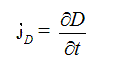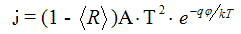Плотность тока смещения в чем измеряется
Плотность тока проводимости, смещения, насыщения: определение и формулы
В данной статье мы рассмотрим плотность тока и формулы для нахождения различных видов плотности тока: проводимости, смещения, насыщения.
Плотность тока – это векторная физическая величина, характеризующая насколько плотно друг к другу располагаются электрические заряды.
Плотность тока проводимости
Ток проводимости – это упорядоченное движение электрических зарядов, то есть обыкновенный электрический ток, который возникает в проводнике. В большинстве случаев, когда речь заходит о токе, имеют ввиду именно ток проводимости.
В данном случае плотность тока – это векторная характеристика тока равная отношению силы тока I в проводнике к площади S поперечного сечения проводника (перпендикулярному по отношению к направлению тока). Эта величина показывает насколько плотно заряды располагаются на всей площади поперечного сечения проводника. Она обозначается латинской буквой j. Модуль плотности электрического тока пропорционален электрическому заряду, который протекает за определенное время через определенную площадь сечения, расположенную перпендикулярно по отношению к его направлению.
Если рассмотреть идеализированной проводник, в котором электрический ток равномерно распределен по всему сечению проводника, то модуль плотности тока проводимости можно вычислить по следующей формуле:
j – Плотность тока [A/м 2 ]
S – Площадь поперечного сечения проводника [м 2 ]
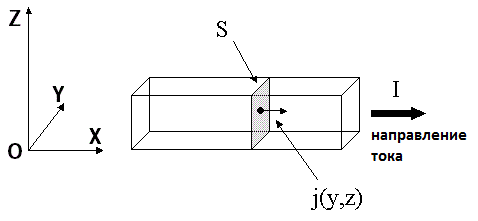
Исходя из этого мы можем представить силу тока I как поток вектора плотности тока j, проходящий через поперечное сечение проводникаS. То есть для вычисления силы тока, текущей через определенное поперечное сечение нужно проинтегрировать (сложить) произведения плотности тока в каждой точке проводника jn на площадь поверхности этой точки dS:
Исходя из предположения, что все заряженные частицы двигаются с одинаковым вектором скорости v, имеют одинаковые по величине заряды e и их концентрация n в каждой точке одинаковая, получаем, что плотность тока проводимости j равна:
j – плотность тока [А/м 2 ]
e – величина заряда [Кл]
v – скорость, с которой движутся частицы [м/с]
Плотность тока смещения
ds – площадь поверхности [м 2 ]
Плотность тока смещения определяется по следующей формуле:
Плотность тока насыщения
В физической электронике используют понятие плотности тока насыщения. Эта величина характеризует эмиссионную способность металла, из которого сделан катод, и зависит от его вида и температуры.
Плотность тока насыщения выражается формулой, которая была выведена на основе квантовой статистики Ричардсоном и Дешманом:
j – плотность тока насыщения[А/м 2 ]
Понравилась статья, расскажите о ней друзьям:
Ток смещения
Что такое ток смещения
Ток смещения или абсорбционный ток — величина, которая прямо пропорциональна скорости изменения электрической индукции.
Каждому переменному магнитному полю свойственно вихревое электрическое поле. Проводя исследования разных электромагнитных процессов, Дж. К. Максвелл определил существование обратного явления, когда электрическое поле, изменяясь, приводит к появлению вихревого магнитного поля.
Данное утверждение является одним из основных в теории Максвелла. Известно, что магнитное поле является признаком любого тока. Основываясь на данном факте, ученый определил переменное электрическое поле, как ток смещения. При измерении он будет отличаться от тока проводимости, который представляет собой следствие движения заряженных частиц в виде электронов и ионов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Токи смещения можно наблюдать только тогда, когда электрическое смещение \(\vec
Вывод данного физического содержания теории Максвелла о токах смещения позволяет утверждать, что переменные электрические поля являются источниками переменных магнитных полей. Следует отметить, что для определения плотности тока смещения используют производную вектора \(\vec
Ток смещения в диэлектрике
Вектор электрической индукции измеряется по формуле:
Где \(\varepsilon _<0>\) — электрическая постоянная, \(\vec \) — вектор поляризации. Уравнение для тока смещения будет иметь следующий вид: Где \(\frac
Токи поляризации являются следствием движения связанных заряженных частиц, которые не обладают принципиальными отличиями по сравнению со свободными зарядами. Основываясь на данном факте, можно объяснить порождение магнитного поля токами поляризации. Принципиальной новизной отличается вторая часть уравнения тока смещения:
Данная формула не обладает связью с перемещением заряженных частиц, но также формирует магнитное поле. Можно сделать вывод, что в вакуумной среде любое изменение электрического поля по времени является причиной образования магнитного поля.
Нужно обратить внимание на то, что определение тока смещения для диэлектриков имеет какое-то обоснование, так как в них действительно можно наблюдать смещение зарядов в атомах и молекулах. Но этот термин применяют и к вакууму, в котором отсутствуют заряды, а, следовательно, и их смещение.
Полный ток
При наличии в проводнике переменного тока, внутри него будет образовано переменное электрическое поле. Таким образом, проводник будет вмещать в себе ток проводимости (j) и ток смещения. Магнитное поле проводника рассчитывают, как сумму вышеуказанных токов, то есть полный ток:
Роль данных слагаемых определяется двумя факторами:
В зависимости от перечисленных характеристик можно наблюдать следующие процессы:
Поэтому величина полного тока может быть меньше, либо превышать ток проводимости, а также равняться нулю. Таким образом, в общем случае переменных токов полный ток определяет магнитное поле. При размыкании контура на концах проводника наблюдают обрыв только тока проводимости. В диэлектрике между концами проводника возникает ток смещения, замыкающий ток проводимости. В итоге, из понятия электрического тока, как полного тока, вытекает утверждение, что в природе все токи замкнуты.
Как найти плотность тока смещения, формула
С целью установить количественную связь между изменяющимся электрическим полем и магнитным полем, которое вызвано электрическим, Максвелл ввел в рассмотрение ток смещения. Определение справедливо в случае работы с диэлектриками. В данных веществах заряженные частицы меняют положение по причине воздействия на них электрического поля.
В случае вакуумной среды заряды отсутствуют, хотя магнитное поле существует. То есть термин «тока смещения» не совсем удачный, однако его смыл абсолютно верный. Вывод, который сделал ученый, состоит в том, что любое переменное электрическое поле образует переменное магнитное поле. Токи проводимости в условиях проводника будут замкнуты токами смещения в диэлектрике или в вакууме. Переменным электрическим полем в конденсаторе создается такое же магнитное поле, как если бы между пластинами был ток проводимости, по величине равный току в металлическом проводнике.
Исходя из данного пояснения, можно рассчитать ток смещения. Поверхностная плотность поляризационных зарядов и вектор электрического смещения равны:
\(\sigma =E\varepsilon \varepsilon _<0>\)
\(\vec
Величину полного заряда на поверхности диэлектрика, а также на пластинах конденсатора, можно рассчитать по формуле:
Где S — площадь обкладки конденсатора.
Тогда можно записать следующую формулу:
Таким образом, ток смещения является величиной, пропорциональной скорости, с которой изменяется вектор электрического смещения \(\vec
Отсюда вытекает определение тока смещения. Плотность тока смещения можно найти по формуле:
Вихревое магнитное поле \(\vec\) образуется в результате протекания тока смещения, связано с направлением вектора \(\frac
Где х — диэлектрическая восприимчивость среды.
В таком случае, можно получить уравнение:
\(D=\varepsilon \varepsilon _<0>E=(1+x)\varepsilon _<0>E\)
\(D=\varepsilon _<0>E+\varepsilon _<0>Ex\)
Вектор поляризации равен:
Таким образом, получим равенство:
Плотность тока смещения в вакууме:
Плотность тока поляризации:
Плотность тока обусловлена перемещением зарядов в диэлектрике.
Токи смещения, абсорбции и сквозной проводимости




Токи смещения, абсорбции и сквозной проводимости
Трайк сначала резко увеличивается, затем постепенно уменьшается, асимптотически приближаясь к значению постоянного установившегося состояния(рис. 3.3). Резкое увеличение тока в начале и его последующее уменьшение вызвано током смещения 1 см в диэлектрике. Плотность тока смещения USM определяется скоростью изменения вектора электрического смещения D (или вектора E, D=eoee): jCM=dD/dr=£OE(dE/dt). (3.4) ток смещения / см обусловлен как мгновенной (деформированной)
поляризацией, так и запаздывающей (ослабленной) поляризацией, а также перераспределением свободного заряда-их дрейфом, но не поляризацией. Людмила Фирмаль
В первом случае из-за короткого периода установления электронной и ионной поляризации/см невозможно зафиксировать с помощью измерительного прибора. Ток смещения, индуцированный поляризационным вариантным типом, является существенным в работе р-р-перехода в полупроводниковых приборах и подробно рассматривается в главе 8.6. Во втором случае ток смещения наблюдается в техническом диэлектрике от нескольких минут до нескольких десятков минут после подачи напряжения, называемого током поглощения / AB.
Ток поглощения 1А обусловлен типом поляризационной релаксации и перераспределением свободного заряда диэлектрического объема. Последнее приводит к накоплению носителей заряда в местах наибольшей концентрации дефектов решетки, неоднородностей, ловушек типа интерфейсов (уровней захвата). Это способствует поляризации организма. При поляризации диэлектрика на поверхности, обращенной к электроду, образуется поверхностно связанный заряд (см. главу 2.1.2). Для того чтобы компенсировать эти заряды на электродах, далее протекают сторонние заряды+0D и — (?)d (см. 2.1, J) образование и рост связаны с возникновением и ростом токов поглощения.
В диэлектриках возникает электрическое поле (ЭКФ), вектор которого направлен в противоположную сторону от приложенного магнитного поля. Если внешний источник напряжения от него и его короткозамкнутого выключается, а в паттерне идет обратный так называемый ток деполяризации, который образуется в результате высвобождения носителя в различные ловушки, то временная зависимость тока деполяризации включает информацию о молекулярной подвижности, структурных дефектах и в некоторых случаях предсказывает закономерность протекания тока полимерного диэлектрика или генерируется термически стимулированный ток деполяризации (ТДК).
Метод ТСД широко применяется при изучении релаксационных переходов (ТС, ТТ и др.). В законах накопления и движения полимерных диэлектриков, а также носителей заряда. Людмила Фирмаль
Составляющая тока, которая не изменяется при подаче постоянного напряжения, представляет собой постоянный поток заряженных частиц, разряженных в электрод, называемый сквозным током 1СК (сквозным током, током утечки или остаточным током), а величина сквозного тока определяет удельную объемную (или поверхностную) проводимость диэлектрика. Ток проводимости обусловлен направленным движением свободного заряда за счет обязательного разряда на электроде. Эти заряды питаются ионообразующими примесями, самими диэлектриками, и инжектируются с электродов сильным магнитным полем.
Только в результате разряда носителя заряда на электродах внешнего контура (положительные ионы принимают электроны с катода, отрицательные ионы излучают электроны на анод), если ток, протекающий в диэлектрике, имеет ионную величину, то во внешнем контуре-электроны. В результате ток преобразуется из ионного типа в электронный на электроде. Ток сквозной проводимости измеряется при подаче на образец постоянного напряжения, а затем ток поглощения падает почти до нуля. Это время, как упоминалось выше, составляет от нескольких минут до нескольких десятков минут и определяется экспериментально.
71 величина проникающего тока при длительном приложении постоянного напряжения может существенно изменяться в результате электрохимического процесса, а также образования объемного заряда. Величина сквозного тока не изменяется только при чисто электронных видах проводимости. Когда постоянное напряжение непрерывно прикладывается к твердому или жидкому диэлектрическому току, проходящему через проводимость, оно продолжает уменьшаться со временем (см. Рисунок). 3. 3, кривая 2), это означает, что электропроводность этого материала в основном обусловлена примесными ионами и снижается в результате электрической очистки образца.
Кроме того, проникающий ток уменьшается, если носители заряда, приближающиеся к электродам, не разряжаются над ними из-за высокого потенциального барьера на границе металл-диэлектрик. Накапливаясь в области вблизи электрода, носитель заряда образует объемный заряд (положительный на катоде, отрицательный на аноде), который препятствует прохождению тока. Объемный заряд области вблизи электрода также может формироваться (в сильном магнитном поле) в результате инжекции заряда с электрода, но в этом случае знак объемного заряда не совпадает с полярностью электрода.
Перед подачей электрического поля диэлектрик электрически нейтрален, то есть суммарный заряд всех малых объемов равен нулю, а после приложения электрического поля заряд (электрод или образец поляризуется) на макроскопическом расстоянии. Разряженный на электроде заряд образует ток сквозной проводимости. Таким образом, поляризация и проводимость всегда появляются одновременно, и через некоторое время поляризация завершается, а проводимость сохраняется. Если ток сквозной проводимости увеличивается со временем(см. Рисунок). 3.3, кривая 7), что указывает на участие в формировании тока заряда, являющегося структурным элементом материала.
При этом хронологический возраст материала-в нем происходит необратимый электрохимический процесс, постепенно приводящий к разрушению (разложению) образца (см. Главу 5). Например, прикладывая постоянное напряжение к нагретому неорганическому стеклу, дендрит может расти по всей толщине диэлектрика от катода к аноду и образовывать проводящий канал через ответвление отложений продукта — достаточное время прохождения тока за счет того, как электролитические продукты в стекле, особенно металлический натрий, выделяющийся на катоде, являются проводящими.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Ток смещения
Вы будете перенаправлены на Автор24
Физическое содержание тока смещения
Любое переменное магнитное поле порождает вихревое электрическое поле. Исследуя разные электромагнитные процессы, Максвелл сделал вывод о том, что существует обратное явление: изменение электрического поля вызывает появление вихревого магнитного поля. Это одно из основных утверждений в теории Максвелла.
Готовые работы на аналогичную тему
Ток смещения в диэлектрике
По определению вектора электрической индукции ($\overrightarrow
Однако, надо заметить, что сам термин «ток смещения» для диэлектриков имеет какое-то обоснование, так как в них действительно происходит смещение зарядов в атомах и молекулах. Но этот термин применяется и к вакууму, где зарядов нет, значит, нет их смещения.
Полный ток
В том случае, если в проводнике течет переменный ток, то внутри него имеется переменное электрическое поле. Значит, в проводнике существует ток проводимости ($j$) и ток смещения. Магнитное поле проводника определено суммой вышеназванных токов, то есть полным током ($\overrightarrow
В зависимости от электропроводности вещества, частоты переменного тока, слагаемые в выражении (4), играют разную роль. В веществах с хорошей проводимостью (например, металлах) и при низких частотах переменного тока плотность тока смещения невелика, тогда как ток проводимости существенен. В таком случае, током смещения пренебрегают, в сравнении с током проводимости. В веществах с высоким сопротивлением (изоляторах) и при больших частотах тока ведущую роль играет ток смещения.
Оба слагаемых в выражении (4) могут иметь одинаковые знаки и противоположные. Следовательно, полный ток может быть и больше и меньше тока проводимости, может даже быть равен нулю.
Значит, в общем случае переменных токов магнитное поле определяется полным током. Если контур разомкнут, то на концах проводника обрывается только ток проводимости. В диэлектрике между концами проводника присутствует ток смещения, который замыкает ток проводимости. Получается, что если под электрическим током понимать полный ток, то в природе все токи замкнуты.
Задание: Плоский конденсатор заряжен и отключен от источника заряда. Он медленно разряжается объемными токами проводимости, которые появляются между обкладками, так как присутствует небольшая электрическая проводимость. Чему равна напряжённость магнитного поля внутри конденсатора? Считать, что краевых эффектов в конденсаторе нет.
Решение:
Ток смещения можно найти как:
В соответствии с законом сохранения заряда, можно записать, что:
Для нашего плоского конденсатора, учитывая полученные выражения (1.3), (1.4), имеем:
Ответ: Магнитное поле в конденсаторе равно нулю.
Решение:
Электрические токи, которые текут от (или к ) шару, возбуждают магнитное поле. Определим направление вектора магнитной индукции этого магнитного поля.
Для устранения полученного противоречия следует предположить, что магнитные поля порождаются не только токами проводимости. Добавим к току проводимости ток смещения ($I_
Ток проводимости, который течет от заряженного шара можно выразить как:
Из выражения (2.3) следует, что:
В соответствии с законом Кулона заряженного проводящего шара, имеем:
\[Q=4\pi r^2D\ \left(2.6\right).\]
Найдем производную по времени от заряда, получим:
Плотность тока смещения при этом будет равна:
Полученное выражение совпадает с определением плотности тока смещения.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 02 03 2021
9.2. Ток смещения
Дж.К. Максвелл (рис. 9.2) был первым, кто задался вопросом о модификации четвертого утверждения. Никаких экспериментальных фактов, к этому подводящих, в то время известно не было. Из четвертого утверждения следует, что токи, порождающие вихревое магнитное поле, должны быть замкнутыми, они нигде не могут прерываться. Действительно, на один и тот же контур L можно натянуть множество поверхностей S. Пусть, скажем, мы выберем две из них — S1 и S2. Так как левая часть (9.4) для них одинакова, то будут равны и правые части. Это значит, что весь ток, вошедший через S1, должен выйти через поверхность S2. Так с обычными токами и происходит. Но бывают нестационарные случаи, когда в каких-то точках меняется плотность электрического заряда. Линии тока будут кончаться в этих местах, что противоречит (9.4).
Рис. 9.2. Дж.К. Максвелл (1831–1879) — английский физик и математик
Чтобы проиллюстрировать подобные случаи, рассмотрим уже знакомый процесс разрядки конденсатора. Пусть имеются две пластины с зарядами +q и –q. Пока цепь разомкнута, равные и разноименные заряды создают в пространстве между пластинами постоянное электрическое поле. Ток по проводам не идет, и вокруг цепи нет магнитного поля (рис. 9.3-1).
Рис. 9.3. Токи смещения в конденсаторе: 1 — начальное состояние конденсатора, 2 — изменение поля в процессе разрядки. Производная напряженности электрического поля по времени направлена в ту же сторону, что и вектор плотности тока, и равна ему по величине
При разрядке конденсатора через проводник, соединяющий пластины, потечет ток от Р к N (рис. 9.3-2). Уменьшение заряда на пластине на величину dq означает, что это же количество электричества протечет по проводу, подсоединенному к пластине (закон сохранения заряда).
Рис. 9.4. Обкладки конденсатора отмечены синим. Поверхность S2 состоит из плоской поверхности, параллельной обкладкам конденсатора и боковой цилиндрической поверхности
которое мы хотели бы проверить на непротиворечивость.
Интегрируем его по поверхности S1 (рис. 9.4). Получаем
Из этого равенства обычно получают величину магнитного поля B для бесконечно длинного проводника. Напомним, что поверхность, по которой ведется интегрирование, может иметь любую форму, при условии, что она опирается на контур G. Воспользуемся этим и интегрируем это же уравнение (9.8) по поверхности S2. Получаем
Здесь краевыми эффектами пренебреженно, Интеграл по боковой (цилиндрической) поверхности равен нулю, если выбрать радиус цилиндра достаточно большим. Выражения (9.9) и (9.10) противоречат друг другу. Значит, уравнение (9.8) неверно и его надо изменить. Простейший путь — добавить в правую часть уравнения (9.8) неизвестный вектор, который мы обозначим как
Найдем неизвестный вектор 
— вместе с (9.8a) получили уравнение Максвелла
Максвелл назвал величину
плотностью тока смещения:
Так как численные значения плотности тока смещения jсм и плотности тока проводимости j равны, то, следовательно, линии плотности тока проводимости внутри проводника непрерывно переходят в линии плотности тока смещения между пластинами (обкладками конденсатора).
Если ввести понятие полного тока, который включает в себя сумму тока проводимости и тока смещения, то для его плотности имеем
На примере конденсатора мы обнаружили, что полный ток будет замкнут: его линии продолжаются, нигде не прерываясь (даже в пространстве между пластинами конденсатора). По этому своему свойству именно полный ток должен стоять в правой части уравнения (рис. 9.5). В этом и состояла идея Максвелла.
Рис. 9.5. Лампочка, подключенная к сети переменного тока через конденсатор,
постоянно горит, так как ток проводимости внутри проводника переходит в ток смещения между пластинами конденсатора
В результате мы можем сформулировать (рис. 9.6)
Утверждение 4.
Вихревое магнитное поле создается полным током, то есть током проводимости и током смещения, вызванным изменяющимся электрическим полем.
Рис. 9.6. Гипотеза Максвелла. Изменяющееся электрическое поле порождает вихревое магнитное поле
Математическим выражением этого утверждения является уравнение, получаемое из (9.11),
Таким образом, Максвелл предсказал новое явление, в известном смысле обратное электромагнитной индукции. Эксперимент подтвердил, что магнитное поле действительно может создаваться изменяющимся во времени электрическим полем (рис. 9.7).
Рис. 9.7. Переменное электрическое поле между пластинами конденсатора порождает вихревое магнитное поле, которое измеряется с помощью проволочной квадратной рамки и отображается на экране монитора
В ряду этих экспериментов первым и главным было экспериментальное доказательство существования электромагнитных волн, выполненное немецким физиком Генрихом Герцем в 1888 году (рис. 9.8). Интересно, что сам Герц не верил в их существование и своими экспериментами хотел опровергнуть теорию Максвелла, созданную им за 20 лет до этого в 1865 году.
Герц не только экспериментально доказал существование электромагнитных волн, но впервые начал изучать их свойства — поглощение и преломление в разных средах, отражение от металлических поверхностей и т. п. Ему удалось измерить на опыте длину волны и скорость распространения электромагнитных волн, которая оказалась равной скорости света (рис. 9.9).
Опыты Герца сыграли решающую роль для доказательства и признания электромагнитной теории Максвелла. Через семь лет после этих опытов электромагнитные волны нашли применение в беспроводной связи, продемонстрированной А.С. Поповым в 1895 г. (рис. 9.10).
Рис. 9.10. А.С. Попов (1859–1905) — русский физик и электротехник
Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент p(t) которого быстро изменяется во времени. Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны λ (рис. 9.11).
Рис. 9.11. Элементарный электрический диполь, совершающий гармонические колебания
Рис. 9.12 дает представление о структуре электромагнитной волны, излучаемой таким диполем.
Рис. 9.12. Излучение элементарного электрического диполя. Дипольный момент направлен вдоль оси z, силовые линии электрического поля лежат в плоскости листа, а силовые линии магнитного поля перпендикулярны плоскости листа
Следует обратить внимание на то, что максимальный поток электромагнитной энергии излучается в плоскости, перпендикулярной оси диполя. Вдоль своей оси диполь не излучает энергии. Герц использовал элементарный диполь в качестве излучающей и приемной антенн при экспериментальном доказательстве существования электромагнитных волн.