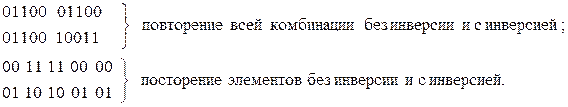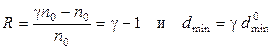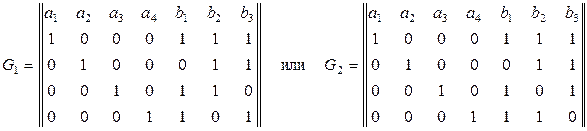по степени помехозащищенности двоичные коды делятся на
Помехоустойчивое кодирование с иcпользованием различных кодов
Это продолженеие статьи о помехоустойчивом кодировании, которая очень долго лежала в черновиках. В прошлой части нет ничего интересного с практической точки зрения — лишь общие сведения о том, зачем это нужно, где применяется и т.п. В данной части будут рассматриваться некоторые (самые простые) коды для обнаружения и/или исправления ошибок. Итак, поехали.
Попытался все описать как можно легче для человека, который никогда не занимался кодированием информации, и без каких-либо особых математических формул.
Когда мы передаем сообщение от источника к приемнику, при передаче данных может произойти ошибка (помехи, неисправность оборудования и пр.). Чтобы обнаружить и исправить ошибку, применяют помехоустойчивое кодирование, т.е. кодируют сообщение таким образом, чтобы принимающая сторона знала, произошла ошибка или нет, и при могла исправить ошибки в случае их возникновения.
По сути, кодирование — это добавление к исходной информации дополнительной, проверочной, информации. Для кодирования на передающей стороне используются кодер, а на принимающей стороне — используют декодер для получения исходного сообщения.
Избыточность кода — это количество проверочной информации в сообщении. Рассчитывается она по формуле:
k/(i+k), где
k — количество проверочных бит,
i — количество информационных бит.
Например, мы передаем 3 бита и к ним добавляем 1 проверочный бит — избыточность составит 1/(3+1) = 1/4 (25%).
Код с проверкой на четность
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка.
Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10010 (изменились 2 и 3 биты)
В принятых данных число единиц четно, и, следовательно, декодер не обнаружит ошибку.
Так как около 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций.
Код Хэмминга
первый проверочный бит на 2 0 = 1;
второй проверочный бит на 2 1 = 2;
третий проверочный бит на 2 2 = 4;
r1 = i1 + i2 + i4
r2 = i1 + i3 + i4
r3 = i2 + i3 + i4
В принципе, работа этого алгоритма разобрана очень детально в статье Код Хэмминга. Пример работы алгоритма, так что особо подробно описывать в этой статье не вижу смысла. Вместо этого приведу структурную схему кодера: 
и декодера 
(может быть, довольно запутано, но лучше начертить не получилось)
e0,e1,e2 опрделяются как функции, зависящие от принятых декодером бит k1 — k7:
e0 = k1 + k3 + k5 + k7 mod 2
e1 = k2 + k3 + k6 + k7 mod 2
e2 = k4 + k5 + k6 + k7 mod 2
Набор этих значений e2e1e0 есть двоичная запись позиции, где произошла ошибка при передаче данных. Декодер эти значения вычисляет, и если они все не равны 0 (то есть не получится 000), то исправляет ошибку.
Коды-произведения
В канале связи кроме одиночных ошибок, вызванных шумами, часто встречаются пакетные ошибки, вызванные импульсными помехами, замираниями или выпадениями (при цифровой видеозаписи). При этом пораженными оказываются сотни, а то и тысячи бит информации подряд. Ясно, что ни один помехоустойчивый код не сможет справиться с такой ошибкой. Для возможности борьбы с такими ошибками используются коды-произведения. Принцип действия такого кода изображён на рисунке: 
Передаваемая информация кодируется дважды: во внешнем и внутреннем кодерах. Между ними устанавливается буфер, работа которого показана на рисунке: 
Информационные слова проходят через первый помехоустойчивый кодер, называемый внешним, т.к. он и соответствующий ему декодер находятся по краям системы помехоустойчивого кодирования. Здесь к ним добавляются проверочные символы, а они, в свою очередь, заносятся в буфер по столбцам, а выводятся построчно. Этот процесс называется перемешиванием или перемежением.
При выводе строк из буфера к ним добавляются проверочные символы внутреннего кода. В таком порядке информация передается по каналу связи или записывается куда-нибудь. Условимся, что и внутренний, и внешний коды – коды Хэмминга, с тремя проверочными символами, то есть и тот, и другой могут исправить по одной ошибке в кодовом слове (количество «кубиков» на рисунке не критично — это просто схема). На приемном конце расположен точно такой же массив памяти (буфер), в который информация заносится построчно, а выводится по столбцам. При возникновении пакетной ошибки (крестики на рисунке в третьей и четвертой строках), она малыми порциями распределяется в кодовых словах внешнего кода и может быть исправлена. 
Назначение внешнего кода понятно – исправление пакетных ошибок. Зачем же нужен внутренний код? На рисунке, кроме пакетной, показана одиночная ошибка (четвертый столбец, верхняя строка). В кодовом слове, расположенном в четвертом столбце — две ошибки, и они не могут быть исправлены, т.к. внешний код рассчитан на исправление одной ошибки. Для выхода из этой ситуации как раз и нужен внутренний код, который исправит эту одиночную ошибку. Принимаемые данные сначала проходят внутренний декодер, где исправляются одиночные ошибки, затем записываются в буфер построчно, выводятся по столбцам и подаются на внешний декодер, где происходит исправление пакетной ошибки.
Использование кодов-произведений многократно увеличивает мощность помехоустойчивого кода при добавлении незначительной избыточности.
Помехоустойчивое кодирование. Коды Хэмминга
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
По используемому алфавиту:
Блочные коды делятся на
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Помехозащищенные коды
Принципы построения помехозащищенных кодов. Простые числовые комплектные коды при числе символов m и числе элементов n0 позволяют образовать 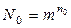
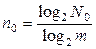
Коды, в которых используется совокупность всех комбинаций минимальной длины, называют минимальными или кодами безызбыточности. Их отдельные комбинации могут отличаться друг от друга всего в одном элементе. Искажение какого-либо одного элемента в результате воздействия помехи приводит к изменению передаваемой комбинации и, следовательно, к ошибке. Для оценки помехозащищенности пользуются кодовым расстоянием d — числом разрядов, в которых элементы одной кодовой комбинации отличаются от другой. Кодовое расстояние может быть определено сложением обеих комбинаций по модулю 2 (mod 2) так, как это показано в табл. 6.2 (сложение по mod 2 обозначают знаком 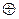
В сумме комбинаций будут нули в тех разрядах, где символы в обеих комбинациях одинаковы, а единицы — где символы различные. Расстояние между различными кодовыми комбинациями из заданного набора наглядно иллюстрируется матрицей кодовых расстояний. Пусть, например, дан некоторый произвольный набор комбинаций: 1) 1000; 2) 1100; 3) 0101; 4) 1111. Определим, например, кодовое расстояние между каждой парой комбинаций в некотором их произвольном наборе (табл. 6.3).
Кодовое расстояние между комбинациями 1 и 2 равно 1, между комбинациями 2 и 3 равно 2 и т. д. В первом случае комбинации могут переходить одна в другую уже при одиночной ошибке, во втором — минимум при тройной. Для повышения помехозащищенности кода необходимо увеличивать минимальное кодовое расстояние dmin.
Существуют два основных подхода к формированию помехозащищенного кода: выбор из заданного набора (множества) безызбыточного кода комбинаций (слов) помехозащищенного кода с заданными свойствами; непосредственное преобразование k-значных комбинаций безызбыточного кода в (n > k)-значную комбинацию помехозащищенного кода с заданными свойствами.
Таблица 6.2 Таблица 6.3
| x | y | x  y y | Номер кодовой комбинации | Кодовые расстояния между комбинациями |
| – | ||||
| – | – | |||
| – | – | – |
В обоих случаях длина слов помехозащищенного кода оказывается большей, чем у безызбыточного кода с таким же набором комбинаций. Поэтому такие коды называют кодами с избыточностью. Пусть у безызбыточного кода длина кодового слова n0, тогда у избыточного кода она больше: n = n0 + Dn. При сравнении кодов избыточность оценивают коэффициентом избыточности R:
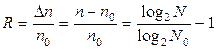
Коды с обнаружением и исправлением ошибок. Чтобы обнаружить ошибку, возникающую в одном символе, достаточно увеличить минимальное кодовое расстояние до dmin = 2. При этом декодирующее устройство будет реагировать только на заданный набор комбинаций, запрещая исполнение всех других, отличающихся от них по крайней мере на единицу. Для обнаружения одновременной ошибки в двух элементах кода кодовое расстояние должно быть увеличено до dmin = 3, в трех элементах до dmin = 4 и т. д. Таким образом, для обнаружения ошибок кратностью sоб нужно иметь минимальное кодовое расстояние dmin ≥ sоб + 1. При d > 2 можно не только обнаруживать, но и исправлять ошибки. Способность кода обнаруживать и исправлять ошибки определяется минимальным кодовым расстоянием d = sи + sоб + 1, где sи — число исправляемых ошибок (sи ≤ sоб). Если исправляются все обнаруженные ошибки, то d = 2sи + 1. Отсюда для исправления одиночной ошибки dmin = 3.
Среди помехоустойчивых кодов различают блочные и непрерывные.
К блочным относятся коды, с помощью которых сообщения передаются блоками из некоторого конечного числа символов. Из них равномерные коды имеют постоянное число символов в комбинации (например, код Бодо), неравномерные — различное (например, код Морзе). Непрерывные коды являются непрерывной последовательностью информационных и проверочных разрядов. Места этих разрядов определяются рекуррентными выражениями. Четкое разделение кодовых комбинаций отсутствует. Блочные коды могут быть разделимыми и неразделимыми. У разделимых кодов разряды четко делятся на информационные и проверочные, причем места проверочных разрядов в кодовой комбинации строго определены. У неразделимых, например у равновесного кода, такого деления нет.
Разделимые коды включают две группы: систематические и несистематические. К систематическим относятся коды, у которых сумма по модулю 2 двух разрешенных комбинаций является комбинацией того же кода. Их примером являются коды Хэминга и циклические коды. К несистематическим кодам относятся код, в котором проверочная комбинация является суммой единиц в информационной части, и код с проверкой на четность.
Если при формировании помехозащищенного кода ставится только задача получения dmin, то наиболее общим является табличный метод. В головку таблицы выписывают комбинации исходного безызбыточного кода. В левый столбец записывают комбинации ошибок для каждого кодового расстояния. Под каждой комбинацией исходного кода записывают искаженные комбинации, возникающие при одиночной, двойной и других ошибках. Первую комбинацию в исходном коде выбирают произвольно. Затем вычеркивают комбинации, в которые первая переходит при числе искажений, равном заданному или меньше его. Из оставшихся невычеркнутых комбинаций произвольно выбирают еще одну; вновь из оставшихся вычеркивают комбинации, отстоящие на dmin — 1, и т. д.
Например, возьмем в качестве исходного двоичный код с n = 3 (табл. 6.4). Пусть надо выбрать кодовые комбинации с dmin = 2 (тогда d = dmin — 1 = 1).
В качестве первой комбинации выбираем 001 (очередность выбора комбинации обозначена цифрой над ней: 001 1 — первая).
В исходном коде вычеркиваем комбинации, расположенные в столбце ниже выбранной (000, 011 и 101). Выбираем следующую комбинацию 010 и дополнительно к уже вычеркнутым 000 и 011 исключаем комбинации 110 (вычеркнутые комбинации обозначены знаком *). Остаются не исключенными комбинации 100 и 111. Таким образом, выбранный набор 001, 010, 100, 111.
Нетрудно убедиться, что между оставшимися комбинациями dmln= 2. Аналогично можно построить код с dmln = 3, если учесть двойные ошибки, и с любым другим dmln.
Практически такой метод можно реализовать только при относительно небольшом числе разрядов, иначе таблица будет очень громоздкой. При значительном числе разрядов комбинацию можно выбрать с помощью вычислительной машины. Недостатком рассмотренного метода является также произвольный выбор первой и последующих комбинаций.
Коды с обнаружением ошибок. В телемеханике используют коды с проверкой на четность, двоичный код на одно сочетание, код с повторением и др.
Таблица 6.4
| Комбинации ошибок | Искаженные комбинации при исходном коде | |||||
| 001 1 | 010 2 | 011* | 100 3 | 101* | 110* | 111 4 |
| d = 1 | ||||||
| d = 2 | ||||||
| … | … | … | … | … | … | |
| … | … | … | … | … |
Код с проверкой на четность может быть получен двумя способами. Первый способ представляет собой вариант табличного метода и состоит в том, что все комбинации двоичного кода разбиваются на две группы, в одну из которых входят комбинации с четным, а в другую — с нечетным числом единиц:
| Комбинации с четным числом единиц |
| То же с нечетным числом единиц |
Для передачи сообщений используют комбинации первой или второй группы.
Код может быть получен с помощью линейных математических преобразований (второй способ). Все элементы исходной кодовой комбинации по mod 2 суммируются. Если сумма равна 1, то для получения четных комбинаций к исходной добавляется еще единица; если же сумма равна 0, то добавляется 0 (для получения нечетных комбинаций делается наоборот). Пример такого кода приведен в табл. 6.5.
Таблица 6.5
| Исходная комбинация | Сумма элементов по модулю 2 | Полученная комбинация |
1 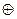 1 1 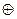 1=1 1=1 | ||
1 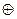 1 1 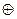 1=0 1=0 |
Код имеет dmin = 2, он может обнаружить любое одиночное искажение, а также все искажения нечетной кратности.
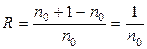
Двоичный код на одно сочетание выполняется выбором из двоичного кода на все сочетания комбинаций с одинаковым числом единиц (l). Такой код также называют равновесным: 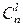
| 1) 11000 | 3) 10010 | 5) 01100 | 7) 01001 | 9) 00101 |
| 2) 10100 | 4) 10001 | 6) 01010 | 8) 00110 | 10) 00011 |
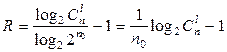
Код обнаруживает любые одиночные искажения, а также многие двойные, тройные и другие искажения.
Коды с повторением предусматривают повторение каждой комбинации 2 раза или более. Такие коды могут быть в двух вариантах: повторение без инверсии и повторение с инверсией. Повторяться могут целые комбинации или отдельные элементы. Например, комбинация 01100 в таких кодах представляется таким образом:
Число элементов n и кодовое расстояние d увеличиваются пропорционально кратности повторения g:
где 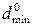
При двукратном повторении безызбыточного кода обнаруживаются все одиночные искажения, все ошибки нечетной кратности и многие другие. Код с повторением и с инверсией более целесообразен при несимметричном канале, в котором чаще появляются ошибки одного знака.
Линейные коды
В устройствах передачи информации широко распространены линейные коды, способные обнаруживать и исправлять ошибки. Они состоят из информационных и проверочных символов и являются разделимыми. Проверочные символы представляют собой различные линейные комбинации информационных символов. При декодировании проверяются линейные соотношения между символами.
Групповые коды. Для двоичных кодов в качестве линейной операции принято посимвольное сложение по модулю 2. Коды, построенные таким образом, называют групповыми, так как они образуют алгебраическую группу по отношению к этой операции (группой называется множество элементов с одной алгебраической операцией: сложение или умножение и т. д.). Каждая кодовая комбинация при этом является суммой по модулю 2 некоторых двух других кодовых комбинаций.
Групповые коды обозначают n, k, d, где n — общее число разрядов; k — число информационных разрядов; d — кодовое расстояние. Наиболее распространен способ задания таких кодов с помощью таблиц — «порождающих» или «базисных» матриц с числом строк k и рядов n. Например, для кода 7, 4, 3 «порождающие» матрицы G имеют вид:
Матрица может быть составлена из любого набора кодовых векторов при условии, что сумма по модулю 2 любых сочетаний векторов не равняется нулевому вектору. При этом те или иные кодовые комбинации из общего числа 2 k могут быть получены суммированием по модулю 2 различных сочетаний строк порождающей матрицы.
Таким образом, для каждого n, k, d кода может быть получено то или иное число вариантов. Все варианты эквивалентны по вероятности правильного приема, но могут иметь различные по степени сложности кодирующие и декодирующие устройства.


Число информационных символов для N сообщений определяется из условия k ≥ log2 N. Зная k и соотношение между z и n, можно определить число контрольных символов:
В качестве примера рассмотрим процесс передачи и приема одной из комбинаций кода 7, 4, 3. Пусть была передана комбинация
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | . |
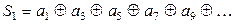
Второй проверке подвергаются разряды, номер которых в двоичной системе имеет единицу во втором разряде:
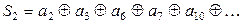
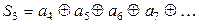
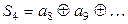
а2 = 1, а4 = 1. Допустим, что в результате искажения на приемной стороне принята комбинация 0101110 (искажение на пятой позиции). Тогда
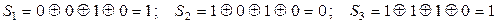
Полученный синдром S3S2S1 → 101 (пять в десятичной системе, и следовательно, ошибочно принят пятый элемент комбинации а5). Исправив его (с 1 на 0), окончательно получим 0101010.
Пусть искажение произошло в проверочном разряде, например, в а4. Тогда будет принята комбинация 010010. При этом S1 = 0; S2 = 0; S3 = 1, т. е. S3S2S1 → 100, а значит, искажен символ а4. Коррекция в этом случае не нужна, так как комбинация исходного кода принята правильно.
Синтез циклических кодов осуществляют алгебраическими методами, отображая кодовые комбинации полиномами. При этом цифры разрядов двоичного кода рассматривают, как коэффициенты при переменной х. Например 100101 ® 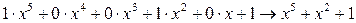
Для получения циклического кода сначала выбирают безызбыточный двоичный код, число разрядов k в комбинациях которого обеспечивает передачу заданного объема сообщений (2 k ). Этому коду соответствует полином G(х) степени (k — 1). Например, кодовая комбинация 1111 отображается полиномом G(х) = х 3 + х 2 + х + 1. При этом полный объем сообщений будет содержать 2 4 = 16 кодовых комбинаций (включая комбинацию 0000).
Длина комбинации помехозащищенного кода должна содержать большее число разрядов n = k + r, где r — число проверочных символов.
Известны различные способы формирования циклических кодов. Рассмотрим один из них, при котором в сформированных комбинациях коэффициенты при высших степенях полинома (от n до n — k) соответствуют информационным разрядам, а при низших (n — k — 1 и ниже) — проверочным.
В качестве порождающего полинома выбирают сомножитель РS(х), имеющий степень r ≤ n — k. При таком полиноме для формирования кодовых комбинаций циклический код при r ≥ 2 будет обнаруживать все одиночные и двойные ошибки, а также все групповые ошибки с числом искаженных символов r и менее. Порождающий полином вида PS(x) = 1 + х позволяет обнаружить все одиночные и любое число нечетных ошибок.
Из всех ошибок длиной r + 1 разрядов не обнаруживается 1/2 r – 1 часть, а при длине большей, чем r + 1, 1/2 r часть.
Для получения помехозащищенной кодовой комбинации F(х) произведение G(х)х r делят на PS(x). Остаток от деления R(х) суммируют с произведением G(х)х r : F(х) = G(х)х r + R(х). Полученная комбинация делится на полином PS(x) без остатка.
Операции, необходимые для получения помехозащищенного кода, выполняются соответствующими аппаратными или программными средствами.
Рассмотрим пример формирования помехозащищенного кода на основе безызбыточного четырехразрядного кода. Пусть исходная комбинация отображается полиномом G(х) = х 3 + х 2 + х + 1, число проверочных символов r = 3.
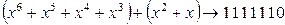
Кодовые комбинации также принимаются с помощью деления на порождающий полином. При отсутствии ошибки принятая комбинация F’ (х) делится на него без остатка. Наличие остатка говорит об ошибке F’ (х) = F (х) + + Е (х), где Е (х) — полином ошибки.
При соответствующем выборе порождающего полинома по величине Е(х) можно не только обнаружить ошибку, но и скорректировать ее.
6.5 Методы повышения достоверности передачи кодированной информации
Повышение достоверности передачи в локальных сетях. В локальных сетях дальность передачи информации сравнительно невелика (в пределах одного или нескольких зданий, расположенных на одной территории). При этом организуют последовательный обмен информацией между ЭВМ и периферийными устройствами, образующими локальную сеть. Для передачи по линии связи исходный безызбыточный код (рис. 6.1, а) преобразуется в серии электрических импульсов. С целью повышения достоверности передачи вносят избыточность с помощью изменения формы сигнала или скорости его передачи.
В качестве примера рассмотрим некоторые виды сигнальных кодов (иногда называемых в литературе «линейными», т. е. предназначенными для передачи по линии). Исходный код, обычно называемый NRZ (non return to zero), применяемый в униполярной форме (в виде импульсов тока одного знака), является непомехозащищенным. Лучшими свойствами (при той же энергии сигнала) обладает биполярный код NRZ, где символ 1 передается импульсом положительной, а символ 0 импульсом отрицательной полярности (рис. 6.1, б). Избыточность достигается за счет наличия двух уровней сигнала различной полярности (+U и – U). Код «Манчестер 11» (рис. 6,1, в) является биполярной сигнальной формой упоминавшегося ранее кода, в котором символ 1 преобразуется в комбинацию 10, а символ 0 — в комбинацию 01. При этом, как и в биполярном коде NRZ, символ передается импульсом положительной, а символ 0 — импульсом отрицательной полярности. Здесь вносится дополнительная избыточность за счет уменьшения скорости передачи информации. Ошибка может быть обнаружена при посимвольном приеме. Ее критерием является заданное превышение продолжительности действия какого-либо из уровней сигнала над временем передачи одного сигнального бита. Положительным свойством кода является несложность обеспечения ввода в синхронизм системы передачи.
В сигнальном коде AMI (alternate mark inversion) (рис. 6.1, г) избыточность вносится с помощью использования (в простейшем случае) трех
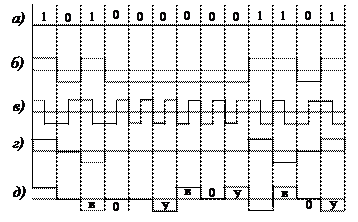 |
 |
|
Рис. 6.1. Примеры кодов последовательного интерфейса ЭВМ
уровней сигнала. При этом символы 0 кодируются отсутствием тока, а символы 1 — его наличием с попеременной инверсией полярности. Ошибка обнаруживается при пропуске инверсного импульса.
При использовании простейшего кода AMI возникает сложность в обеспечении ввода системы передачи в синхронизм при передаче длинных последовательностей нулевых символов. В связи с этим более широко распространены его формы, называемые BNZS, где цепочки из N нулей заменяют подстановками знакопеременных символов. Так, в коде BNZS цепочки из трех последовательных нулей заменяют подстановкой BOV или OOV (рис. 6.1, д), где В, V соответственно импульсы, кодируемые по правилам кода AMI и с нарушением этих правил. При выборе вида подстановки необходимо, чтобы число импульсов В между двумя последовательно расположенными импульсами V было нечетным и чередовалась полярность импульсов V. Существуют и другие формы сигнальных кодов.
Внесение асимметрии в канал передачи и применение пошаговой синхронизации. Повышение помехозащищенности при передаче кодовых комбинаций по линии связи может быть достигнуто применением пошаговой синхронизации и широтно-импульсной модуляции с контролем длительности импульсов. Пошаговая синхронизация позволяет обеспечить четкость синхронной работы передающего и приемного устройства и числовой защиты. Различие в длительности передачи символов 1 и 0 позволяет свести к нулю трансформацию вида 1 → 0 и обеспечить dmin = 2 даже при передаче исходного безызбыточного кода. Наличие числовой защиты контроля длительности импульсов и пошаговой синхронизации существенно сокращает возможность приема ложных комбинаций при групповых ошибках.
Использование обратного канала. Различают системы с решающей и информационной обратной связью. В системах с решающей обратной связью приемное устройство по избыточности, заложенной в кодовую комбинацию, определяет, относится она к разрешенным или нет. Если да, то приемник исполняет команду и по каналу обратной связи передает уведомление об исполнении. Запрещенную комбинацию приемник не исполняет, а по обратному каналу посылает сигнал переспроса, по которому передается повторное сообщение.
В системах с информационной обратной связью приемник, приняв сообщение, передает его же по обратному каналу. Передающее устройство сравнивает переданное им сообщение с информацией, полученной по каналу обратной связи. При совпадении результатов сравнения передается сигнал, разрешающий исполнение; при несовпадении — сигнал запрета. При необходимости передача повторяется заданное число раз. В простых системах телеуправления при этом обычно используют двоичные неизбыточные коды. В сложных системах с большим объемом передаваемой информации применяют побайтную передачу с контролем по паритету каждого байта и с числовой защитой в конце серии. Это позволяет обнаруживать ошибки в приеме того или иного байта, не дожидаясь окончания передачи всего сообщения.
Мажоритарное декодирование. При этом методе в канал связи передается не менее трех одинаковых кодовых комбинаций. Решение о правильности принимается по большинству одинаковых принятых комбинаций. Например, если переданы три комбинации и на приемной стороне две из них совпали, то разрешается исполнение команды («метод голосования»).
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.059 сек.)