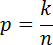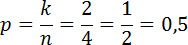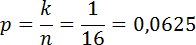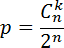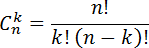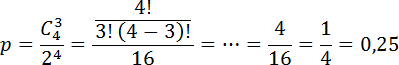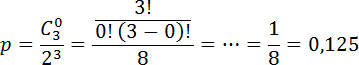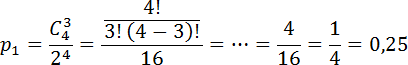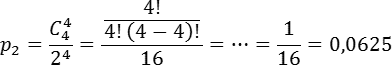Подбрасывают 3 монеты найти вероятность того что выпадут три герба

Бросание монет. Решение задач на нахождение вероятности

Кстати, сразу упомяну, что в контексте подобных задач не существенно, написать «бросают 3 монеты» или «бросают монету 3 раза», результат (в смысле вычисления вероятности) будет один и тот же (так как результаты бросков независимы друг от друга).

1. Классическое определение вероятности

Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Пример 2. Дважды бросают симметричную монету. Найти вероятность того, что оба раза выпала одна сторона.

Как видим, все довольно просто. Перейдем к чуть более сложной задаче.

Пример 3. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.

Взяли разгон и переходим к 4 монетам.

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Думаю, к этому времени вы уже поняли суть метода и сможете сами решить задачи, где бросаются 2-3-4 монеты и орел не выпадает ни разу, или решка ровно один раз и т.п.

2. Комбинаторика + классическая вероятность

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Конечно, этот подход кажется сложнее из-за более формального математического описания решения, но гораздо легче масштабируется.

Например, если рассмотреть подобную задачу:

Пример 5. Монету бросают 8 раз. Найти вероятность того, что герб выпадет ровно 4 раза

Ради полноты изложения приведу еще пример задачи, решаемой подобным образом (но если хотите, можете сразу переходить к более простому способу 3).

Пример 6. Монету подбрасывают 6 раз. Найти вероятность того, что гербы выпадут два раза и только подряд, а в остальные разы будут только решки.

Способ 3. Формула Бернулли

А теперь все задачи решаются проще простого, вот глядите!

Пример 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Пример 4. Монету бросают 4 раза. Найти вероятность того, что герб выпадет от 2 до 3 раз.

Пример 7. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.

Пример 8. Пусть бросают 8 монет. Найти вероятность того, что орел не менее 7 раз.

Таким образом, используя одну простейшую формулу, можно решать множество задач, причем неважно, 3 монеты бросается, или 30, сложность расчетов примерно одинакова. Но, если число бросков становится очень большим, удобнее использовать приближенные формулы Муавра-Лапласа, о которых можно узнать здесь.

Полезные ссылки

Решебник по вероятности

А здесь вы найдете более 200 задач о бросании монет с полными решениями (вводите часть текста для поиска своей задачи):

Источник

Задачи B6 с монетами

Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:

где искомая вероятность, число устраивающих нас событий, общее число возможных событий.

Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа В этом и состоит вся сложность.

Тем не менее, существует как минимум два принципиально различных метода решения:

Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!

Метод перебора комбинаций

Этот метод еще называется «решение напролом». Состоит из трех шагов:

К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:

Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.

Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):

Итого варианта. Теперь выпишем те варианты, которые подходят по условию задачи:

Таких вариантов оказалось Находим вероятность:

Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем все возможные комбинации орлов и решек:

OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP

Всего получилось вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, Осталось найти вероятность:

Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.

Специальная формула вероятности

Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:

Теорема. Пусть монету бросают Тогда вероятность того, что орел выпадет ровно можно найти по формуле:

Где C_n k — число сочетаний которое считается по формуле:

Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.

На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.

Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.

По условию задачи, всего бросков было Требуемое число орлов: Подставляем в формулу:

С тем же успехом можно считать число решек: Ответ будет таким же.

Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем числа Поскольку монету бросают 3 раза, А поскольку решек быть не должно, Осталось подставить числа в формулу:

Напомню, что 0! = 1 по определению. Поэтому C ₃ 0 = 1.

Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.

Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.

Пусть вероятность того, что орел выпадет 3 раза. Тогда Имеем:

Теперь найдем вероятность того, что орел выпадет все 4 раза. В этом случае Имеем:

Чтобы получить ответ, осталось сложить вероятности p ₁ и p ₂. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:

p = p ₁ + p ₂ = 0,25 + 0,0625 = 0,3125

Источник

Подбрасывают 3 монеты найти вероятность того что выпадут три герба

3.1.1 жПТНХМБ вЕТОХММЙ

1. тБУУНПФТЙН НПДЕМШ ПДОПЗП ЙУРЩФБОЙС У ДЧХНС ЙУИПДБНЙ: ω₁, ω₂.

рТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ Ч ЬФПН УМХЮБЕ ВХДЕФ ЙНЕФШ ЧЙД:

ч ЛБЮЕУФЧЕ F ЧПЪШНЕН НОПЦЕУФЧП ЧУЕИ РПДНОПЦЕУФЧ:

чЕТПСФОПУФШ ЧЧЕДЕН ФБЛ:
т(ω₁) = p; P(ω₂) = g, p + g = 1.

2. тБУУНПФТЙН НПДЕМШ ДЧХИ ОЕЪБЧЙУЙНЩИ ЙУРЩФБОЙК У ФЕНЙ ЦЕ ЙУИПДБНЙ: ω₁, ω₂ ДМС ЛБЦДПЗП ЙЪ ОЙИ.

рТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ Ч ЬФПН УМХЮБЕ ВХДЕФ ЙНЕФШ ЧЙД:

бОБМПЗЙЮОП, НПЦОП РПУФТПЙФШ НПДЕМЙ ДМС 3-И, 4-И Й ВПМЕЕ ОЕЪБЧЙУЙНЩИ ЙУРЩФБОЙК.

3. тБУУНПФТЙН НПДЕМШ n ОЕЪБЧЙУЙНЩИ ЙУРЩФБОЙК У ФЕНЙ ЦЕ ДЧХНС ЙУИПДБНЙ ω₁, ω₂ ДМС ЛБЦДПЗП ЙЪ ОЙИ.

рТПУФТБОУФЧП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ Ч ЬФПН УМХЮБЕ ЙНЕЕФ ЧЙД:

ъБНЕФЙН, ЮФП ЬМЕНЕОФБТОЩЕ УПВЩФЙС ТБЪМЙЮБАФУС ЛБЛ РПТСДЛПН РПСЧМЕОЙС ω₁, ω₂, ФБЛ Й ЙИ ЮЙУМПН.

фБЛ ЛБЛ ЙУРЩФБОЙС ОЕЪБЧЙУЙНЩЕ (ФП ЕУФШ ТЕЪХМШФБФ ЛБЦДПЗП ЙЪ ОЙИ ОЕ ЪБЧЙУЙФ ПФ ТЕЪХМШФБФПЧ РТЕДЩДХЭЙИ), ФП

Й УМЕДПЧБФЕМШОП, ТЕЪХМШФБФ ЪБЧЙУЙФ ФПМШЛП ПФ ЮЙУМБ РПСЧМЕОЙК ω₁ Й ω₂.

ъБНЕФЙН, ЮФП ЬМЕНЕОФБТОЩИ УПВЩФЙК, УПУФПСЭЙИ Ч ФПН, ЮФП РТЙ n ЙУРЩФБОЙСИ РПСЧЙФУС ТПЧОП m ХУРЕИПЧ, ВХДЕФ НОПЗП, Б ЙНЕООП: — ЮЙУМП УРПУПВПЧ ТБУУФБЧЙФШ m ПДЙОБЛПЧЩИ РТЕДНЕФПЧ РП n НЕУФБН.

фептенб 3.1.1.1 (жПТНХМБ вЕТОХММЙ)
» m п Z: 0 ≤ m ≤ n

ъбнеюбойе. ъБНЕФЙН, ЮФП

ъбдбюб 3.1.1.1 нПОЕФХ РПДВТБУЩЧБАФ 8 ТБЪ. лБЛПЧБ ЧЕТПСФОПУФШ, ЮФП ПОБ 6 ТБЪ ХРБДЕФ ЗЕТВПН ЧЧЕТИ?

n = 8, m = 6; p = 1/2, g = 1/2; P₈(6) = (1/2) 6 (1/2) 2 = 7/64.

ъбдбюб 3.1.1.2 дЧБ ТБЧОПУЙМШОЩИ РТПФЙЧОЙЛБ ЙЗТБАФ Ч ЫБИНБФЩ. юФП ЧЕТПСФОЕЕ: ЧЩЙЗТБФШ ДЧЕ РБТФЙЙ ЙЪ ЮЕФЩТЕИ ЙМЙ ЮЕФЩТЕ ЙЪ ЧПУШНЙ (ОЙЮШЙ ОЕ ХЮЙФЩЧБАФУС)?

т₄(2) = (1/2) 2 (1/2) 2 = 3/8 = 0,375;

т₈(4) = (1/2) 4 (1/2) 4 = 35/128 ≈ 0,273.

уМЕДПЧБФЕМШОП, ЧЕТПСФОЕЕ ЧЩЙЗТБФШ ДЧЕ РБТФЙЙ ЙЪ ЮЕФЩТЕИ.

ъбдбюб 3.1.1.3 нПОЕФХ ВТПУБАФ 5 ТБЪ. оБКФЙ ЧЕТПСФОПУФШ ФПЗП, ЮФП ЗЕТВ ЧЩРБДЕФ:

Б) НЕОЕЕ ДЧХИ ТБЪ; В) ОЕ НЕОЕЕ ДЧХИ ТБЪ.

Б) т₅(m 5 + (1/2)(1/2) 4 = 3/16.

ъбдбюб 3.1.1.5 пФТЕЪПЛ бч, ДМЙОБ ЛПФПТПЗП 15УН, ТБЪДЕМЕО ФПЮЛПК у Ч ПФОПЫЕОЙЙ 2:1. оБ ЬФПФ ПФТЕЪПЛ ОБХДБЮХ ВТПЫЕОЩ 4 ФПЮЛЙ. оБКФЙ ЧЕТПСФОПУФШ ФПЗП, ЮФП ДЧЕ ЙЪ ОЙИ ПЛБЦХФУС МЕЧЕЕ ФПЮЛЙ C Й ДЧЕ РТБЧЕЕ ФПЮЛЙ у.

P = P₄(2) = (2/3) 2 (1/3) 2 = 8/27.

ъБДБЮЙ ДМС УБНПУФПСФЕМШОПЗП ТЕЫЕОЙС.

ъбдбюб 3.1.1.1(у) дЧБ ТБЧОПУЙМШОЩИ РТПФЙЧОЙЛБ ЙЗТБАФ Ч ЫБИНБФЩ. юФП ЧЕТПСФОЕЕ ЧЩЙЗТБФШ: Б) ПДОХ РБТФЙА ЙЪ ДЧХИ ЙМЙ ДЧЕ РБТФЙЙ ЙЪ ЮЕФЩТЕИ; В) ОЕ НЕОЕЕ ДЧХИ РБТФЙК ЙЪ ЮЕФЩТЕИ ЙМЙ ОЕ НЕОЕЕ ФТЕИ РБТФЙК ЙЪ РСФЙ (ОЙЮШЙ ЧП ЧОЙНБОЙЕ ОЕ РТЙОЙНБАФУС)?

ъбдбюб 3.1.1.2(у) оБКФЙ ЧЕТПСФОПУФШ ФПЗП, ЮФП УПВЩФЙЕ б РПСЧЙФУС ОЕ НЕОЕЕ ФТЕИ ТБЪ Ч ЮЕФЩТЕИ ОЕЪБЧЙУЙНЩИ ЙУРЩФБОЙСИ, ЕУМЙ ЧЕТПСФОПУФШ РПСЧМЕОЙС УПВЩФЙС б Ч ПДОПН ЙУРЩФБОЙЙ ТБЧОБ 0,4.

© гЕОФТ ДЙУФБОГЙПООПЗП ПВТБЪПЧБОЙС пзх, 2000-2002

Источник

Подбрасывают 3 монеты найти вероятность того что выпадут три герба

Задача 1. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Общее число равновозможных комбинаций может быть четыре:

«орел-орел», «орел-решка», «решка-орел», «решка-решка».

Из них благоприятных исходов по условию задачи два – это «орел-решка» и «решка-орел». Следовательно, искомая вероятность, равна

.

Задача 2. В случайном эксперименте симметричную монету бросают три раза. Найдите вероятность того, что решка выпадет ровно 2 раза.

1-й способ: Решать эту задачу можно аналогично предыдущей. Всего исходов может быть 8:

Благоприятных исходов по условию задачи 3 – это «орел-решка-решка», «решка-орел-решка», «решка-решка-орел». И искомая вероятность равна

.

2-й способ. В рамках данной задачи общее число исходов можно определить по формуле

,

где — число подбрасываний монеты (в данном случае ), а 2 – число возможных исходов при подбрасывании монеты (либо «орел», либо «решка»). Таким образом, сразу получаем число исходов .

Число благоприятных исходов можно определить по формуле

,

где — число выпадения «решки» из подбрасываний. В данной задаче и

.

В итоге получаем искомую вероятность

.

Второй способ может существенно сократить время на решение подобных задач, особенно когда речь идет о четырех и более подбрасываний монеты. В этом случае перебирать все варианты и не ошибиться становится трудно, и применение указанных формул существенно облегчает задачу.

Задача 3. В случайном эксперименте монету бросают трижды. Найдите вероятность того, что решка выпадет ровно три раза.

В данной задаче имеется только один благоприятный исход из восьми равновероятных исходов:

Следовательно, искомая вероятность равна

.

Общее число исходов также можно определить по формуле , приведенной в предыдущей задаче.

Задача 4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно один раз.

Будем считать, что выпадение «орла» соответствует началу игры мячом команды «Изумруд». Тогда задача сводится к определению вероятности выпадения «орла» ровно один раз из трех бросаний монеты.

Всего исходов 8 (см. предыдущие задачи). Из них «орел» выпадет ровно один раз в вариантах – это случаи: «орел-решка-решка», «решка-орел-решка», «решка-решка-орел». Следовательно, искомая вероятность равна

.

Источник