Подбрасывают игральный кубик какова вероятность того что выпавшее количество очков будет нечетным

Решение задач о бросании игральных костей

Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.

Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).

Одна игральная кость

Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?

Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.

Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.

Две игральные кости

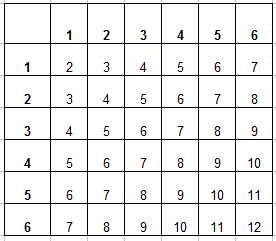
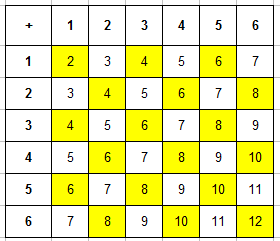
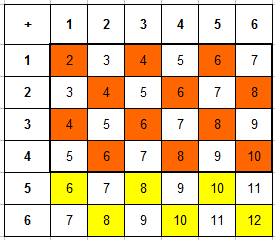
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.

Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:

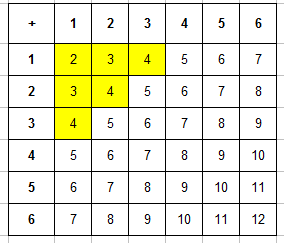
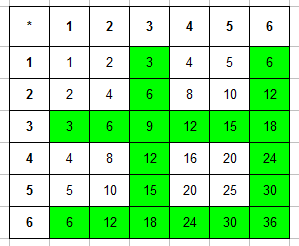
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.

Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:

Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).

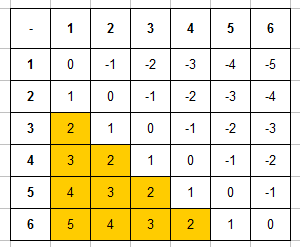
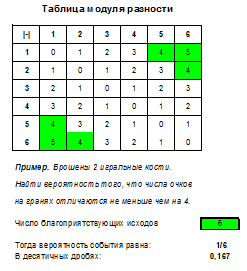
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.

Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:

Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).

Другие задачи про кости и кубики

Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.

Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.

В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.

Теперь подберем такие исходы, которые дают в сумме 15 очков.

Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.

Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.

В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.

Приведем еще пример, решаемый аналогичным образом.

Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.

Полезные ссылки

Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.

В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.

Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.

Еще по теории вероятностей:

В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):

Источник

LiveInternetLiveInternet

—Ссылки

—Рубрики

—Метки

—Приложения

—Поиск по дневнику

—Подписка по e-mail

—Статистика

100 готовых задач по теории вероятностей часть 33

3201. Игральную кость подбрасывают 3 раза. Найти вероятность того, что 1) дважды появится число очков, кратное трем; 2) число очков кратное трем появится хотя бы один раз. Готовое решение задачи

3202. Игральная кость подбрасывается 15 раз. Сколько раз в среднем может появиться 4 на верхней грани. Готовое решение задачи

3203. Игральную кость подбрасывают 3 раза. Найти вероятность того, что при этом шестерка:
а) не выпадет ни разу,
б) выпадет по крайней мере два раза. Готовое решение задачи

3204. Какова вероятность, что при пяти подбрасываниях игральной кости шестерка выпадет три раза. Готовое решение задачи

3205. Игральная кость подбрасывается до тех пор, пока не выпадет 3 раза число очков, отличное от 6. Какова вероятность, что «шестерка» выпадет 3 раза. Готовое решение задачи

3206. Игральная кость подбрасывается до тех пор, пока не выпадет 4 раза число очков, отличное от 6. Какова вероятность, что «шестерка» выпадет 2 раза? Готовое решение задачи

3207. Игральная кость подбрасывается до тех пор, пока не выпадет 6 раз число очков, отличное от 5. Какова вероятность, что будет произведено 9 бросков? Готовое решение задачи

3208. Игральная кость подбрасывается до тех пор, пока не выпадет 5 раз число очков, отличное от 6. Какова вероятность, что будет произведено 8 бросков? Готовое решение задачи

3209. Игральная кость подбрасывается восемь раз. Найти вероятность того, что грань с цифрой 5 выпадет ровно 6 раз. Готовое решение задачи

3210. Игральная кость подбрасывается 9 раз. Найдите вероятность того, что а) шестерка выпадет 3 раза; б) шестерка выпадет более 3 раз; в) шестерка выпадет не более семи. Готовое решение задачи

3211. Определить вероятность того, что при пятикратном бросании игральной кости четное число очков выпадает не менее трех раз (следует учесть, что «не менее трех раз» означает 3, 4 или 5 раз (в пяти бросаниях), т.е., рассматривается сумма несовместных событий). Готовое решение задачи

3212. Определить вероятность того, что при пятикратном бросании шестигранной игральной кости четное число очков выпадает не менее двух раз. Готовое решение задачи

3213. Товаровед осматривает 30 образцов товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,7. Найти наивероятнейшее число образцов, которые товаровед признает годными к продаже. Готовое решение задачи

3214. Испытание заключается в бросании трёх игральных костей. Найти вероятность того, что в пяти независимых испытаниях ровно два раза выпадет по три единицы. Готовое решение задачи

3215. Испытание состоит в бросании 3 игральных костей. Найдите вероятность того, что в 5 независимых испытаниях ровно 3 раза выпадет по 3 единицы. Готовое решение задачи

3216. Игральная кость подброшена 3 раза. Найдите вероятность того, что четное число очков не выпадет ни разу. Готовое решение задачи

3217. Бросают пять игральных костей. Чему равна вероятность того, что из пяти выпавших цифр одна – четная, а все остальные – нечетные? Готовое решение задачи

3218. Какова вероятность того, что при бросании семи игральных костей шестерка выпадет трижды? Готовое решение задачи

3219. Бросают 5 игральных костей. Найти вероятность того, что на трёх из них выпадет 5. Готовое решение задачи

3220. Игральный кубик подбрасывают три раза. Какова вероятность того, что:
а) шестерка не появится ни разу;
б) шестерка появится хотя бы один раз. Готовое решение задачи

3221. Игральная кость подбрасывается 7 раз. Найти вероятность того, что 6 очков выпадет 4 раза. Готовое решение задачи

3222. Игральную кость подбрасывают 7 раз. Найти вероятность того, что одно очко выпадет не более двух раз. Готовое решение задачи

3223. Найти вероятность того, что при пяти бросаниях игральной кости («пятерка») выпадет не более 2-х раз. Готовое решение задачи

3224. Игральную кость бросают 7 раз. Какова вероятность того, что ни разу не выпадет цифра 6. Готовое решение задачи

3225. Игральная кость подбрасывается семь раз. Найти вероятность того, что грань с цифрой два выпадет ровно четыре раза. Готовое решение задачи

3226. Игральную кость бросают 6 раз. Какова вероятность того, что дважды выпадет число очков, делящееся на три? Готовое решение задачи

3227. Игральную кость бросают 5 раз. Какова вероятность, что тройка выпадет дважды? Готовое решение задачи

3228. Игральную кость бросают 6 раз. Какова вероятность того, что четное число очков выпадет трижды? Готовое решение задачи

3229. Игральную кость бросают 6 раз. Какова вероятность того, что нечетное число очков выпадет в два раза чаще, чем четное. Готовое решение задачи

3230. Игральный кубик подбрасывают 4 раза. Какова вероятность того, что «шестерка» выпадет только один раз? Готовое решение задачи

3231. Игральную кость бросают 4 раза. Какова вероятность того, что цифра 3 выпадет 1 раз? Готовое решение задачи

3232. Игральная кость бросается 4 раза. Найти вероятность следующих событий:
а) «шестерка» выпадет 1 раз.
б) число выпавшей «шестерки» будет в пределах от 2 до 4. Готовое решение задачи

3233. Игральная кость бросается 37 раз. Каково наиболее вероятное количество испытаний, в которых выпадет более 4-x очков? Готовое решение задачи

3234. Чему равна вероятность того, что при 10 бросаниях игральной кости выпадет хотя бы один раз единица? Готовое решение задачи

3235. Игральная кость бросается трижды. Определить вероятность того, что: а) хотя бы один раз выпадет 5 очков; б) три раза выпадет 6 очков; в) два раза выпадет 3 очка. Готовое решение задачи

3236. Найти вероятность того, что при бросании игральной кости три раза не менее 2 раз выпадет 6 очков. Готовое решение задачи

3237. Игральную кость бросают пять раз. Найти вероятность того, что на верхней грани шесть очков при этом выпадет: 1) два раза; 2) более двух раз; 3) менее двух раз. Готовое решение задачи

3238. В урне 6 белых и 5 красных шаров. Случайным образом вынимают 4 шара. Какова вероятность того, что среди них имеется: а) ровно 3 белых шара; б) меньше, чем 3 белых шаров; в) хотя бы 1 белый шар. Готовое решение задачи

3239. В корзине имеется 6 белых и 6 черных шаров. Наудачу извлекается 6 шаров. Какова вероятность того, что это будут 3 белых и 3 черных шара? Готовое решение задачи

3240. В урне содержится 4 черных и 5 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) менее, чем 2 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3241. В корзине имеется 8 белых и 5 черных шаров. Наудачу извлекается 6 шаров. Какова вероятность того, что это будут 4 белых и 2 черных шара? Готовое решение задачи

3242. В урне содержится 7 черных и 4 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) менее, чем 2 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3243. В корзине имеется 7 белых и 6 черных шаров. Наудачу извлекается 5 шаров. Какова вероятность того, что это будут 2 белых и 3 черных шара? Готовое решение задачи

3244. В урне содержится 6 черных и 7 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 4 белых шара;
б) менее, чем 4 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3245. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 4 белых и 3 черных. Готовое решение задачи

3246. В корзине 9 белых, 6 чёрных и 5 красных шаров. Наудачу извлекают 3 шара. Какова вероятность того, что они одного цвета? Готовое решение задачи

3247. В урне содержится 8 черных и 6 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 3 белых шара;
б) менее, чем 3 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3248. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 1 белый, 1 черный и 5 красных. Готовое решение задачи

3249. В урне содержится 4 черных и 6 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 3 белых шара;
б) менее, чем 3 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3250. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 1 белый, 4 черных и 2 красных. Готовое решение задачи

3251. В урне содержится 8 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) менее, чем 2 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3252. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 5 белых и 2 красных. Готовое решение задачи

3253. В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
а) 4 белых шара;
б) менее, чем 4 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3254. В корзине 20 белых и 5 чёрных шаров. Наудачу берут 4 шара. Какова вероятность того, что 3 белые и 1 черный? Готовое решение задачи

3255. В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров. Найти вероятность того, что среди них имеется:
а) 3 белых шара;
б) менее, чем 3 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3256. В корзине 9 белых, 6 черных и 5 красных шаров. Наудачу извлекают 2 шара. Какова вероятность того, что они одного цвета? Готовое решение задачи

3257. В урне содержится 6 черных и 5 белых шаров. Случайным образом вынимают 4 шаров. Найти вероятность того, что среди них имеется:
а) 2 белых шара;
б) менее, чем 2 белых шара;
в) хотя бы один белый шар. Готовое решение задачи

3258. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 1 белый, 5 черных и 1 красный. Готовое решение задачи

3259. В корзине 9 белых, 6 чёрных и 3 красных шара. Наудачу извлекают 3 шара. Какова вероятность того, что они разных цветов? Готовое решение задачи

3260. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 5 белых, 1 черный и 1 красный. Готовое решение задачи

3261. В корзине 8 белых, 6 чёрных и 5 красных шаров. Наудачу извлекают 3 шара. Какова вероятность того, что они одного цвета? Готовое решение задачи

3262. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 1 белый, 2 черных и 4 красных. Готовое решение задачи

3263. В корзине 9 белых, 6 чёрных и 5 красных шаров. Наудачу извлекают 3 шара. Какова вероятность того, что среди них 2 чёрных и 1 красный? Готовое решение задачи

3264. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 2 белых, 1 черный и 4 красных. Готовое решение задачи

3265. В корзине 20 белых и 5 чёрных шаров. Наудачу берут 5 шаров. Какова вероятность того, что 3 белые и 2 чёрный? Готовое решение задачи

3266. Из корзины, в которой находиться 15 белых и 5 черных шаров, вынимают наудачу 2 шара. Какова вероятность того, что оба шара окажутся черными? Готовое решение задачи

3267. Из корзины, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными? Готовое решение задачи

3268. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 2 белых, 4 черных и 1 красный. Готовое решение задачи

3269. В корзине 9 белых и 5 чёрных шаров. Какова вероятность того, что два вынутых шара, различного цвета? Готовое решение задачи

3270. В корзине 21 шар, среди которых 6 белых, 7 черных и 8 красных. Наудачу извлекают 7 шаров. Найти вероятность того, что 4 белых, 1 черный и 2 красных. Готовое решение задачи

3271. В урне из 30 шаров 5 зеленые. Какова вероятность того, что из 7 наугад выбранных шаров один окажется зеленым? Готовое решение задачи

3272. В урне 2 белых, 3 черных и 5 красных шаров. Три шара вынимают наугад. Найти вероятность того, что среди вынутых шаров хотя бы два будут разного цвета. Готовое решение задачи

3273. В урне 3 белых и 7 черных шаров. Из урны вынимают одновременно два шара. Какое событие более вероятно: A – шары одного цвета, B – шары разных цветов? Готовое решение задачи

3274. В урне находится 25 одинаковых по размеру и внешнему виду шаров: среди них 5 белых и 20 черных. Наугад вынимаются 6 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 3 белых? Готовое решение задачи

3275. В урне находится 20 одинаковых по размеру и внешнему виду шаров: среди них 8 белых и 12 черных. Наугад вынимаются 7 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 6 белых? Готовое решение задачи

3276. В урне находится 28 одинаковых по размеру и внешнему виду шаров: среди них 7 белых и 21 черных. Наугад вынимаются 4 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 3 белых? Готовое решение задачи

3277. В урне находится 16 одинаковых по размеру и внешнему виду шаров: среди них 8 белых 8 черных. Наугад вынимаются 8 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 7 белых? Готовое решение задачи

3278. В урне находится 18 одинаковых по размеру и внешнему виду шаров: среди них 9 белых и 9 черных. Наугад вынимаются 7 шаров (без возвращения в урну). Чему равна вероятность того, что среди них окажется 4 белых? Готовое решение задачи

3279. В урне находятся 31 шар одинакового размера, причем 5 шаров белого цвета, остальные красные. Наудачу вытягивается 8 шаров. Найти вероятность того, что среди вытянутых шаров будет 3 белых. Готовое решение задачи

3280. В урне находятся 13 шаров одинакового размера, причем 5 шаров белого цвета, остальные красные. Наудачу вытягивается 5 шаров. Найти вероятность того, что среди вытянутых шаров будет 4 белых. Готовое решение задачи

3281. В урне 20 шаров одинакового размера, причем 6 шаров белого цвета, остальные красные. Наудачу вытягивается 7 шаров. Найти вероятность того, что среди вытянутых шаров будет 5 белых. Готовое решение задачи

3282. В урне находятся 31 шар одинакового размера, причем 6 шаров белого цвета, остальные красные. Наудачу вытягивается 8 шаров. Найти вероятность того, что среди вытянутых шаров будет 2 белых. Готовое решение задачи

3283. В урне находятся 23 шара одинакового размера, причем 5 шаров белого цвета, остальные красные. Наудачу вытягивается 6 шаров. Найти вероятность того, что среди вытянутых шаров будет 1 белый. Готовое решение задачи

3284. В урне находится десять красных, восемь черных и семь белых шаров. Случайно выбирают шесть шаров. Найти вероятность того, что среди них три красных, два черных и один белый. Готовое решение задачи

3285. В урне 5 белых и 10 черных шаров. Чему равна вероятность того, что, вынув наудачу 4 шара, получим белых:
а) не менее 2,
б) ровно 3. Готовое решение задачи

3286. В урне 6 белых, 4 черных и 5 красных шаров. Из урны наугад вынимают 5 шаров. Найти вероятность того, что среди них окажутся 2 белых и 1 черный шар. Готовое решение задачи

3287. Из урны, в которой находятся 8 черных и 4 белых шара, наугад вынимают 2 шара. Найдите вероятность того, что оба шара окажутся белыми. Готовое решение задачи

3288. В урне 6 черных и 4 белых шаров. Из урны извлекают 3 шара. Найти вероятность того, что среди них будет 1 белый. Готовое решение задачи

3289. В урне 6 черных и 4 белых шара. Из урны вынули 3 шара. Найти вероятность того, что среди них будет 2 белых? Готовое решение задачи

3290. В урне находятся 12 шаров, третья часть которых – красные. Наугад взяли 6 шаров. Найти вероятность того, что 4 из них будут красные. Готовое решение задачи

3291. В урне 5 белых, 6 черных и 9 красных шаров. Из урны наугад извлекаются 3 шара. Какова вероятность того, что все они – разных цветов. Готовое решение задачи

3292. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Готовое решение задачи

3293. В урне 12 белых, 5 красных и 3 черных шара. Наудачу вынимается три шара. Найдите вероятность того, что
а) все шары будут красными?
б) хотя бы один шар будет черным?
в) два шара будут белыми? Готовое решение задачи

3294. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара? Готовое решение задачи

3295. В урне 40 шаров: 15 белых, 15 красных и 10 синих. Найти вероятность появления цветного шара. Готовое решение задачи

3296. В урне находятся 4 черных, 7 красных, 9 зеленых и 11 синих шаров. Оттуда вынули один шар. Найти вероятность появления цветного шара (не черного). Готовое решение задачи

3297. В ящике 20 шаров: 5 белых, 5 синих и 10 красных. Найти вероятность появления цветного шара. Готовое решение задачи

3298. В урне содержится 13 зеленых, 10 желтых, 8 белых шаров. Найдите вероятность появления цветного шара. Готовое решение задачи

3299. В урне 100 шаров, из них 5 белые, остальные – черные. Какова вероятность того, что из 4-х наугад выбранных шаров два окажутся белыми? Готовое решение задачи

3300. В урне 10 шаров, из них 4 белые, остальные – чёрные. Какова вероятность того, что из 3-х наугад выбранных шаров два окажутся белыми? Готовое решение задачи

Источник

Новые задачи по теории вероятностей

Рассмотрим решение новых задач по теории вероятностей, которые появятся в ЕГЭ по математике в 2022 году.

Вы можете попробовать решить задачи самостоятельно, а потом сверить свое решение с предложенным.

1. № 508755

Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что в первый раз выпало 6 очков.

Нам нужно найти вероятность того, что в первый раз выпало 6 очков при условии, что вы сумме выпало 8 очков.

Воспользуемся формулой Байеса.

Пусть событие А «в сумме выпало 8 очков»

Событие В «в первый раз выпало 6 очков И в сумме выпало 8 очков»

Искомая вероятность равна

Если всего в сумме выпало 8 очков, то возможны такие варианты бросков:

Вероятность этого события

В первый раз выпало 6 очков И в сумме выпало 8 очков всего в одном случае, и вероятность этого события равна

Тогда вероятность равна

2. № 508769

Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8».

Представим число 8 в виде суммы двух слагаемых, каждое из которых принимает значения от 1 до 6 (возможное число очков):

По условию задачи сумма (2) нам не подходит.

Сумма (1) выпадает в двух случаях: 2+6 и 6+2.

Сумма (3) выпадает в одном случае.

При бросании кости 2 раза получаем возможных исходов. Из этих исходов вычтем те, при которых выпало 3 очка. Таких исходов 11: 3 очка при первом броске, и 6 вариантов для второго броска, или наоборот. При этом исход 3;3 считаем один раз. Таким образом, имеем 36-11=25 возможных исходов. Для нас благоприятными являются 3 исхода. Таким образом, искомая вероятность равна

3. № 508781

Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

При каждом броске монеты получаем 2 возможных исхода: орел или решка. При броске монеты 11 раз имеем возможных исходов.

Найдем число благоприятных исходов для события А. Оно равно числу способов выбрать из 11 элементов 5. То есть мы ищем число сочетаний из 11 по 5.

Сократим дробь и получим:

Таким образом, .

Найдем число благоприятных исходов для события B. Оно равно числу способов выбрать из 11 элементов 4. То есть мы ищем число сочетаний из 11 по 4.

Сократим дробь и получим:

Таким образом, .

Найдем :

4. № 508791

В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.

Вероятность получить определенную комбинацию очков при одновременном бросании костей такая же, как при их последовательном бросании.

При бросании двух костей имеем возможных исходов.

Найдем число благоприятных исходов в каждой попытке: нас устраивает: если гость выбросит (5 и 6) очков или (6 и 5) очков, то есть 2 благоприятных исхода.

Следовательно, вероятность получить искомую комбинацию в первой попытке равна

Вторая попытка необходима, если первая неудачна. Вероятность того, что первая попытка неудачна, равна

Вторая попытка, то есть одновременное бросание двух костей второй раз ничем не отличается от первой.

Итак, считаем вероятность того, что «искомая комбинация выпала при первой попытке» ИЛИ «искомая комбинация НЕ выпала при первой попытке И выпала при второй попытке».

Вероятность получить искомую комбинацию в первой ИЛИ второй попытке равна сумме вероятностей:

5. № 508793

Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что потребовалось сделать три броска? Результат округлите до сотых.

Заметим, что уже известно, что сумма всех выпавших очков равна 4. Это ограничивает число возможных вариантов бросков.

Рассмотрим все возможные варианты. Для этого представим число 4 в виде различных сумм слагаемых:

Найдем вероятность каждого исхода:

Вероятность того, что в сумме выпадет 4 очка, равна сумме вероятностей всех исходов:

Вероятность того, что в результате трех бросков сумма выпавших очков оказалась равна 4:

Нам нужно найти вероятность того, что сделано 3 броска при условии, что сумма всех выпавших очков равна 4.

Тогда по формуле Байеса

6. № 508798

Игральную кость бросали до тех пор, пока сумма выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось 3 броска? Ответ округлите до сотых.

Можно переформулировать вопрос так: какова вероятность, что сумма выпавших очков станет больше либо равна 4 на третьем броске?

Это возможно в случаях когда в первых двух бросках выпало 1+1, или 1+2, или 2+1. При этом в первом случае на третьем броске должно выпасть не меньше 2. А во втором и третьем случае на третьем броске может любое количество очков, сумма все равно будет больше либо равна 4. Тогда получаем, что вероятность равна

7. № 508809

Телефон передает SMS-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой отдельной попытке, равна 0,2. Найдите вероятность того, что для передачи сообщения потребуется не больше двух попыток.

Если вероятность того, что сообщение удастся передать без ошибок, равна 0,2, следовательно, вероятность того, что сообщение будет передано с ошибкой, равна . Нам надо найти вероятность того, что сообщение будет передано без ошибок в результате первой ИЛИ второй попытки.

Нарисуем дерево вероятностей.

Вероятность того, что сообщение будет верно передано в результате первой попытки, равна 0,2. Вероятность того, что сообщение будет верно передано в результате второй попытки, равна . Следовательно, вероятность того, что сообщение будет передано без ошибок в результате первой ИЛИ второй попытки, равна

.

8. № 508820

При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 91% случаев. Если заболевание нет, то тест выявляет отсутствие заболевания в среднем в 93% случаев. Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание? Результат округлите до сотых.

Нам нужно найти вероятность того, что пациент болен при условии, что известно, что у него ПЦР тест положительный. Пусть вероятность того, что пациент болен , тогда вероятность того, что пациент здоров равна .

Нарисуем дерево вероятностей.

По условию в среднем тест оказывается положительным у 10% пациентов, к исходу «положительный тест» ведут красные линии.

Вероятность того, что пациент имеет положительный тест равна 0,1.

Получаем: если пациент здоров, то вероятность получить положительный тест равна , если пациент болен, вероятность получить положительный тест равна .

Заметим, что вероятность того, что пациент болен И имеет положительный тест равна .

Теперь воспользуемся формулой Байеса. Нам нужно найти отношение вероятности того, что пациент болен И имеет положительный тест к вероятности того, что пациент имеет положительный тест.

9. № 508831

Стрелок в тире стреляет по мишени до тех пор, пока не поразит ее. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,5?

Если стрелок попадает в цель с вероятностью 0,2, то с вероятностью 0,8 он промахивается. Если стрелок промахивается, то он делает следующий выстрел.

Нарисуем дерево вероятностей:

Вероятность попасть в цель в результате одного выстрела равна 0,2.

Вероятность попасть в цель в результате двух выстрелов равна .

Вероятность попасть в цель в результате трех выстрелов равна .

Вероятность попасть в цель в результате четырех выстрелов равна .

10. № 508843

В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что в первый раз синий фломастер появится третьим по счету?

Всего в ящике 6 фломастеров. Первый раз синий фломастер появится третьим по счету, если сначала будут вытащены 2 красных фломастера.

Вероятность первый раз вынуть красный фломастер равна

После этого в ящике останется 2 красных и 3 синих фломастера, всего 5 штук.

Вероятность второй раз вынуть красный фломастер равна

После этого в ящике останется 1 красный и 4 синих фломастера, всего 4 штуки.

Теперь вероятность вынуть синий фломастер равна .

Тогда вероятность того, что в первый раз синий фломастер появится третьим по счету равна произведению вероятностей:

11. №508851

Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно три мишени» больше вероятность события «стрелок поразит ровно две мишени».

Найдем вероятность того, что стрелок поразит мишень первым или вторым выстрелом. Если он попадает в мишень с вероятностью 0,6, то с вероятностью 1-0,6=0,4 он промахивается.

Нарисуем дерево вероятностей:

Мы видим, что вероятность того, что стрелок поразит мишень первым или вторым выстрелом, равна . Отсюда вероятность промахнуться, сделав два выстрела, равна .

Найдем вероятность события «стрелок поразит ровно три мишени». Пусть стрелок первые три мишени поразит, а в последние две промахнется. Вероятность этого события равна . Но он может попадать в цель и промахиваться в произвольном порядке, главное чтобы он три раза попал. Всего число таких комбинаций вариантов «попал в 3 цели и в 2 промахнулся» равно — число способов выбрать из пяти элементов три, (число сочетаний из 5 по 3).

Тогда

Тогда

Найдем отношение :

12. № 508868

В викторине участвуют 10 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых шести играх победила команда А. Какова вероятность, что эта команда выиграет седьмой раунд.

Команда А победила в шести играх, следовательно, она сыграла 6 матчей с шестью командами и оказалась самой сильной из них. В этих матчах приняло участие 7 команд.

Рассмотрим команды, которые уже сыграли. Присвоим каждой команде номер в зависимости от ее силы. Самая сильная команда имеет больший номер. Пусть, например, в нашем случае у команды А будет номер номер 7, а у проигравших команд будут номера от 1 до 6. Вероятность того, что команда А выиграет у всех остальных команд равна вероятности того, из 7 различных чисел у команды А номер 7. Эта вероятность равна .

Теперь нам нужно найти вероятность того, что команда А выиграет седьмой раунд. В седьмом раунде добавится еще одна команда. То есть мы будем иметь уже 8 команд, участвующих в викторине. Теперь у нас уже есть как бы набор из восьми различных чисел, характеризующих силу каждой команды. Найдем вероятность противоположного события: «команда А проиграет седьмой раунд». Это значит, что восьмая команда окажется сильнее, чем команда А. Это произойдет в том случае если из 8 различных неравных чисел у числа, характеризующего силу восьмой команды будет самое большое значение. Вероятность этого события равна .

Отсюда вероятность того, что команда А выиграет седьмой раунд равна

В общем случае получаем, что если команда выиграла в раундах, то вероятность выиграть в -м равна .

13. № 508871

Если в турнире участвуют 8 игроков, то в первом туре будет сыграно 4 партии, во втором 2 и в третьем 1 партия.

Иван и Алексей могут сыграть в первом туре. В первом туре соперником Ивана может быть один из семи игроков, то есть вероятность того, что это Алексей, равна .

Значит, вероятность того, что Иван и Алексей сыграли в первом туре равна .

Если Иван и Алексей не сыграли в первом туре, то они могут сыграть во втором. Для начала они должны выйти во второй тур. Для этого должны быть выполнены два условия: 1) они не сыграли друг с другом в первом туре (вероятность этого события ) И 2) оба победили каждый в своей партии.

Вероятность того, что они выйдут во второй тур равна .

Во второй тур выходят 4 человека, значит, при условии, что Иван и Алексей вышли во второй тур, вероятность сыграть друг с другом равна .

Таким образом, вероятность того, что Иван и Алексей вышли во второй тур И сыграли друг с другом равна .

Вероятность не сыграть друг с другом, при условии, что они вышли во второй тур равна .

Тогда они могут выйти в третий тур. Чтобы они вышли в третий тур необходимо выполнение двух условий: 1) они не сыграли друг с другом в первом туре И выиграли обе партии в первом туре, 2) они не сыграли друг с другом во втором туре И они победили каждый в своей партии во втором туре. Вероятность того, что это произойдет равна

Если они вышли в третий тур, то они точно сыграют друг с другом.

Таким образом, вероятность того, что Иван и Алексей сыграют друг с другом ИЛИ в первом туре, ИЛИ во втором ИЛИ в третьем туре, равна

Графически решение можно изобразить так:

14. № 508887

Первый игральный кубик обычный, а на гранях второго кубика нет четных чисел, а нечетные числа встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность, что бросали второй кубик?

При бросании первого кубика вероятность, что выпадут 3 и 5 очков, ИЛИ 5 и 3 очка равна .

Во втором кубике по две грани с числами 3 и 5, соответственно вероятность, что выпадут 3 и 5 очков, ИЛИ 5 и 3 очка равна .

Получили, что вероятность выпадения указанной комбинации при бросании второго кубика в 4 раза больше, чем при бросании первого. То есть из 5 серии бросков, при которых выпали числа 3 и 5, в среднем в 4-х случаях из пяти это будут броски второго кубика. Следовательно, вероятность того, что бросали второй кубик равна 0,8.

15. № 509078

Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придется купить еще 2 или 3 шоколадных яйца?

По условию покупка одного яйца не принесет Маше принцессу нового вида, то есть вероятность того, что Маша получит такую же принцессу, как у нее уже есть, равна , соответственно, вероятность того, что при покупке одного яйца Маша НЕ получит такую же принцессу, как у нее уже есть, равна .

Маша получит принцессу, отличную от тех, что у нее есть при покупке второго Киндер-сюрприза, если в первом купленном яйце будет такая же принцесса, как у нее есть, а во втором отличная от уже имеющихся. Вероятность этого события равна

Маша получит принцессу, отличную от тех, что у нее есть при покупке третьего Киндер-сюрприза, если в первом и втором купленном яйце будет такая же принцесса, как у нее есть, а в третьем отличная от уже имеющихся. Вероятность этого события равна

Тогда вероятность получить новую принцессу при покупке второго ИЛИ третьего Киндер-сюрприза равна

15. № 508885

Искомая вероятность находится по следующей формуле:

где — вероятность того, что следующий член последовательности на единицу больше предыдущего, . Вывод этой формулы выходит за рамки школьной программы, поэтому просто используем ее для решения задачи:

Источник