Подбросили две игральные кости какова вероятность того что сумма больше 6
Решение задач о бросании игральных костей
Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.
Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).
Одна игральная кость
Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?
Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.
Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.
Две игральные кости
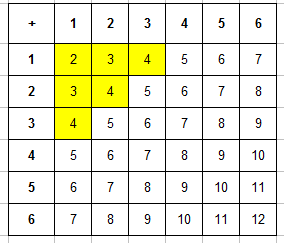
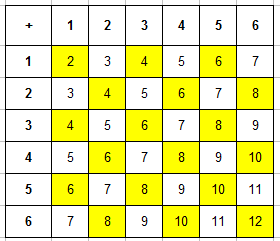
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.
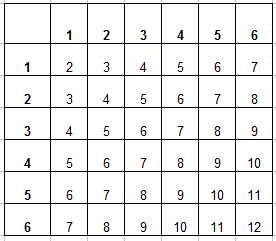
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:
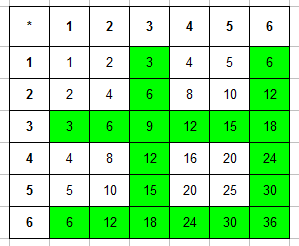
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:
Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).
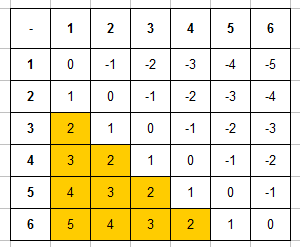
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.
Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:
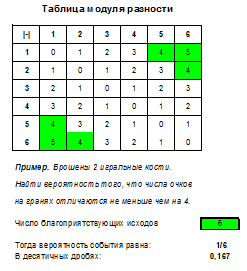
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).
Другие задачи про кости и кубики
Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.
Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.
В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.
Теперь подберем такие исходы, которые дают в сумме 15 очков.
Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.
Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.
В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.
Приведем еще пример, решаемый аналогичным образом.
Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.
Полезные ссылки
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.
В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.
Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.
Еще по теории вероятностей:
В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):
Подбросили две игральные кости какова вероятность того что сумма больше 6
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 5 очков, равно 4: 2+3, 3+2, 4+1, 1+4. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 5 очков, равна
Ответ : 0,11.
Я считая вариантов не 4,а 6,так как 5 и 0 в сумме тоже дадут 5
На игральной кости нет 0.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 6 очков, равно 10: 1 + 1 + 4, 1 + 4 + 1, 4 + 1 + 1, 1 + 2 + 3, 1 + 3 + 2, 3 + 1 + 2, 3 + 2 + 1, 2 + 1 + 3, 2 + 3 + 1, 2 + 2 + 2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6 · 6 · 6 = 216. Следовательно, вероятность того, что в сумме выпадет 6 очков, равна
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 10 очков, равно 3: 4+6, 5+5, 6+4. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 10 очков, равна
Ответ : 0,08.
Ваше решение: Количество исходов, при которых в результате броска игральных костей выпадет 10 очков, равно 3: 4+6, 5+5, 6+4. Я думаю, что будет 4 исхода, так как вероятность что выпадет две пятёрки увеличина вдвое т.к. если бы на однок кости была бы пометочка, то можно было бы видеть, что иногда выпадает 5:5. (с точкой) или 5.:5. Поэтому думаю, что будет 4 варианта 4+6, 5+5, 5+5, 6+4
Максим Ваше рассуждение ошибочно.
Если на одной из костей была бы «пометочка», то вариант 5.:5. невозможен.
Вариант «две пятерки» возможен только в одном случае, если на первом кубике выпадает пятерка и при этом на втором кубике тоже выпадает пятерка.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 2 очка. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 15 очков. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 13 очков. Результат округлите до десятых.
Это задание ещё не решено, приводим решение прототипа.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
Ответ : 0,14.
Задание 10 ЕГЭ по математике. Теория вероятностей. Повышенный уровень сложности
В 2022 году в варианты ЕГЭ по математике добавились новые задачи по теории вероятностей. По сравнению с теми, которые раньше были в варианте, это повышенный уровень сложности.
Мы разберем задачу №10 из Демоверсии ЕГЭ-2022, задания из Методических рекомендаций ФИПИ для учителей и аналогичные им.
1. Демо-версия ЕГЭ-2022
Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало
6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?
Выпишем возможные исходы как тройки чисел так, чтобы в сумме получилось 6.
Всего 10 возможных исходов. Благоприятные исходы помечены красным цветом, их 6.
По определению вероятности получаем
2. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка.
Выпишем возможные варианты получения 8 очков в сумме:
Подходит только вариант 5; 3. Вероятность этого события равна 1 : 5 = 0,2 (один случай из 5 возможных).
3. В ящике 4 красных и 2 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
Благоприятными будут следующие исходы:
Первый раз – вытащили красный фломастер,
И второй раз – красный,
А третий раз – синий.
Вероятность вытащить красный фломастер (которых в ящике 4) равна
После этого в ящике остается 5 фломастеров, из них 3 красных, вероятность вытащить красный равна
Наконец, когда осталось 4 фломастера и из них 2 синих, вероятность вытащить синий равна
Вероятность события <красный – красный – синий >равна произведению этих вероятностей, то есть
4. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Всего в коробке 25 фломастеров.
В условии не сказано, какой из фломастеров вытащили первым – красный или синий.
Предположим, что первым вытащили красный фломастер. Вероятность этого в коробке остается 24 фломастера, и вероятность вытащить вторым синий равна Вероятность того, что первым вытащили красный, а вторым синий, равна
А если первым вытащили синий фломастер? Вероятность этого события равна Вероятность после этого вытащить красный равна вероятность того, что синий и красный вытащили один за другим, равна
Значит, вероятность вытащить первым красный, вторым синий или первым синий, вторым красный равна
А если их доставали из коробки не один за другим, а одновременно? Вероятность остается такой же: 0,3. Потому что она не зависит от того, вытащили мы фломастеры один за другим, или с интервалом в 2 секунды, или с интервалом в 0,5 секунды… или одновременно!
Ответ: 0,3.
5. При подозрение на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.
Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Пациент приходит к врачу и делает ПЦР-тест. Он может быть болен этим заболеванием – с вероятностью х. Тогда с вероятностью 1 – х он этим заболеванием не болен.
Анализ пациента может быть положительным по двум причинам:
а) пациент болеет заболеванием, которое нельзя называть, его анализ верен; событие А,
б) пациент не болен этим заболеванием, его анализ ложно-положительный, событие В.
Это несовместные события, и вероятность их суммы равна сумме вероятностей этих событий.
Мы составили уравнение, решив которое, найдем вероятность x.
Нам же нужно найти вероятность z того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание. Вероятность этого события равна (пациент болен и ПЦР-тест выявил заболевание, произведение событий). С другой стороны, эта вероятность равна (у пациента положительный результат ПЦР-теста, и при выполнении этого условия он действительно болен).
Вероятность того, что пациент с положительным результатом ПЦР-теста действительно болен, меньше половины!
Кстати, это реальная проблема для диагностики в медицине, то есть в задаче отражена вполне жизненная ситуация.
6. Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой следующей попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.
Решение:
Здесь все просто. Либо сообщение удалось передать с первой попытки, либо со второй.
Вероятность того, что сообщение удалось передать с первой попытки, равна 0,4.
С вероятностью 0,6 с первой попытки передать не получилось. Если при этом получилось со второй, то вероятность этого события равна
Значит, вероятность того, что для передачи сообщения потребовалось не более 2 попыток, равна
7. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
А это более сложная задача. Можно, как и в предыдущих, пользоваться определением вероятности и понятиями суммы и произведения событий. А можно применить формулу Бернулли.
Формула Бернулли:
– Вероятность того, что в n независимых испытаниях некоторое случайное событие A наступит ровно m раз, равна:
p – вероятность появления события A в каждом испытании;
– вероятность появления события A в каждом испытании
Коэффициент часто называют биномиальным коэффициентом.
О том, что это такое, расскажем с следующих статьях на нашем сайте. Чтобы не пропустить – подписывайтесь на нашу рассылку.
А пока скажем просто, как их вычислять.
Нет, это не заклинание. Не нужно громко кричать: Эн. Поделить на эм! И на эн минус эм! То, что вы видите в формуле, – это не восклицательные знаки. Это факториалы. На самом деле все просто: n! (читается: эн факториал) – это произведение натуральных чисел от 1 до n. Например,
Пусть вероятность выпадения орла при одном броске монеты равна вероятность решки тоже Давайте посчитаем вероятность того, что из 10 бросков монеты выпадет ровно 5 орлов.
Вероятность выпадения ровно 4 орлов равна
Найдем, во сколько раз больше, чем
8. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности события «стрелок поразит ровно 4 мишени»?
Стрелок поражает мишень с первого или со второго выстрела;
Вероятность поразить мишень равна
Вероятность поразить 5 мишеней из 5 равна
Вероятность поразить 4 мишени из 5 находим по формуле Бернулли:
9. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым выстрелом равна 0,5. Во сколько раз вероятность события «стрелок поразит ровно 3 мишени» больше вероятности события «стрелок поразит ровно 2 мишени»?
Решение:
Найдем вероятность поразить одну мишень – с первого или со второго выстрела.
С вероятностью стрелок поражает мишень первым выстрелом (и больше по ней не стреляет).
Найдем вероятность того, что стрелок поразит мишень вторым выстрелом. Она равна так как с вероятностью он промахнулся в первый раз и с вероятностью второй выстрел был удачным.
Значит, вероятность поразить одну мишень первым или вторым выстрелом равна
Теперь нам на помощь придет формула Бернулли.
Найдем вероятность того, что стрелок поразит ровно 3 мишени из 5.
Вероятность поразить ровно 2 мишени из пяти
10. Стрелок в тире стреляет по мишени. Известно, что он попадает в цель с вероятностью 0,3 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать этому стрелку, чтобы вероятность поражения цели была не менее 0,6?
Вероятность промаха при одном выстреле равна 1 – 0,3 = 0,7.
Если то – не подходит;
Для условие выполнено,
11. Игральную кость бросают до тех пор, пока сумма всех выпавших очков не превысит число 3. Какова вероятность того, что для этого потребуется ровно 3 броска? Ответ округлите до сотых.
Кажется, что задача сложная (на самом деле нет).
Давайте подумаем: как получилось, что ровно за 3 броска игральной кости сумма выпавших очков оказалась больше трех? Из этого следует, что за 2 броска сумма выпавших очков была меньше 3 или равна 3.
Если за 2 броска сумма выпавших очков была меньше 3, значит, она была равна 2, то есть первый раз выпала единица и второй раз тоже единица. Вероятность этого события равна
Сколько же очков в этом случае должен дать третий бросок? Очевидно, что подойдет 2, 3, 4, 5, 6 – все, кроме 1. Вероятность того, что при третьем броске выпадет число очков, не равное единице, равна
Значит, вероятность того, что при первых двух бросках выпали единицы, а при третьем – не единица, равна
Нам подойдет также случай, когда сумма очков за первые 2 броска равна 3. Это значит, что выпали 2 и 1 или 1 и 2, то есть 2 благоприятных исхода из 36 возможных. Вероятность этого события равна
При этом нам все равно, что выпадет при третьем броске: очевидно, что сумма очков при трех бросках будет больше трех.
Вот еще одна задача из Демо-версии ЕГЭ-2022:
12. В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Решение:
Пусть N – численность взрослого населения в городе (мужчин и женщин).
Количество взрослых мужчин в городе: 0,48N
Количество женщин в городе: 0,52N
Из них 0,15 * 0,52N = 0,078N женщин-пенсионеров,
Всего пенсионеров 0,126N,
Тогда количество мужчин-пенсионеров равно 0,126N – 0,078N = 0,048N.
Вероятность для случайно выбранного мужчины оказаться пенсионером равна отношению числа мужчин-пенсионеров к числу мужчин в городе, то есть 0,048 N : 0,48N = 0,1.
Ответ. 0,1.
Мы разобрали все доступные типы заданий №10 из вариантов ЕГЭ-2022. Раздел будет дополняться решениями новых задач– как только они появятся в Банке заданий ФИПИ.
Подбросили две игральные кости какова вероятность того что сумма больше 6
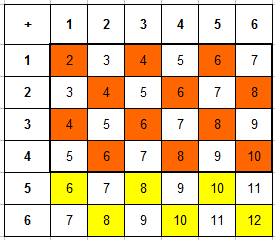
Игральную кость бросили два раза. Известно, что шесть очков не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 2».
Условию, что при двукратном броске игральной кости шесть очков не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 2» соответствует 1 из них (отмечены зелёным цветом). Значит, искомая вероятность равна
Игральную кость бросили два раза. Известно, что два очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 12».
Условию, что при двукратном броске игральной кости два очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 12» соответствует 1 из них (отмечены зелёным цветом). Значит, искомая вероятность равна
Игральную кость бросили два раза. Известно, что два очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 4».
Условию, что при двукратном броске игральной кости два очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 4» соответствуют 2 из них (отмечены зелёным цветом). Значит, искомая вероятность равна
Игральную кость бросили два раза. Известно, что четыре очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 11».
Условию, что при двукратном броске игральной кости четыре очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 11» соответствуют 2 из них (отмечены зелёным цветом). Значит, искомая вероятность равна