Погорелов или атанасян что лучше
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Учебник геометрии Погорелова
| Заслуженный участник |
Последний раз редактировалось arqady 20.10.2019, 23:56, всего редактировалось 1 раз.
| Заслуженный участник |
А мне нравился Погорелов. И геометрия по нему тоже. И сейчас прочитала эту заметочку и думаю, да неужели же правда, быть того не может, чтобы про наклонную и перпендикуляр да из теоремы Пифагора. Наверное, думаю, другой у нас Погорелов был.
Последний раз редактировалось eugensk 21.10.2019, 05:05, всего редактировалось 11 раз(а).
Неравенство треугольника да, после независимости косинуса от треугольника, абсолютной геометриии практически нет. Зато без перегибаний плоскости, которые не походили на строгие рассуждения.
Мне Погорелов всегда нравился, возможно я предпочел бы учебник где неравенство треугольника идёт вначале, но только при условии что будут хорошие школьные аксиомы для перегибаний и наложений.
| Заслуженный участник |
Последний раз редактировалось wrest 21.10.2019, 11:11, всего редактировалось 1 раз.
| Модератор |
| Заслуженный участник |
Последний раз редактировалось vpb 21.10.2019, 16:48, всего редактировалось 1 раз.
А между тем теорема о вертикальных углах, я где-то видел, считается первой теоремой, с которой началась доказательная математика. И доказал ее Фалес 26 веков назад. Думаю, так же, как и во всех учебниках с тех пор она доказывалась (и в Киселеве, и в Погорелове, и в Атанасяне, и в 100500 предшествующих).
Т.е. я хочу сказать, что в сравнении с перлами Колмогорова то, что Погорелов выводит «перпендикуляр короче наклонной» из Пифагора, выглядит невинной шуткой.
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
Если имеется в виду его «Алгебра и начала анализа», то полностью согласен. Я почти застал время, когда он был в двух отдельных книжках: одна для 9-го класса, другая для 10-го. До сих пор помню приятные впечатления от теории пределов последовательностей.
А вот про его геометрию ничего не помню и ничего (ни хорошего, ни плохого) сказать не могу.
| Заслуженный участник |

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Погорелов или атанасян что лучше
Войти
Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal
Обзор учебников геометрии 7-9 классы
7–9 классы. Геометрия
Эти трудности произрастают из желания автора все вывести из аксиом и не пользоваться, например, наложением при доказательстве признаков равенства треугольников. Обучающий и воспитательный эффект от такого способа обучения не сопоставим с испытываемыми трудностями. Но наличие жесткой и экономной системы изложения и последовательной системы упражнений делает учебник лаконичным.
Учебник Л.С. Атанасяна и др. отличается более спокойным отношением к лозунгу «в геометрии все должно быть доказано!» В частности, упомянутые признаки равенства треугольников доказываются наложением треугольников, что представляется оправданным на ранней стадии освоения учащимися нового предмета. Некоторые теоретические факты, используемые в дальнейшем изложении, даны не в виде теорем, а в виде задач, что затрудняет ссылки на них в последующей работе. Теоремы о средней линии треугольника и трапеции могли бы появиться раньше. Но этот момент учитель при желании может компенсировать, предложив учащимся другой способ доказательства в начале 8 класса, а вот изучение площади до подобия оправдано (в учебнике Погорелова порядок обратный).
К учебнику [18] изданы «Дополнительные главы» для учащихся классов с углубленным изучением математики.
Учебник А.Д. Александрова и др. — пример соединения в одном курсе планиметрии и стереометрии. В учебнике имеются обидные неточности, которые не украшают учебник. Определение: «Треугольники называются равными, если равны их стороны». В скобках есть разъяснение формулировки. Но как ученик должен давать определение — с разъяснением или без него? А определение позволяет два равносторонних треугольника назвать равными. Не лучше ли дать нормальную формулировку? Это пример из планиметрии, заметно отличающейся от других курсов, но хорошо выстроенной логически. А стереометрия вся построена на недоказанности — это в учебнике, в котором реализуется аксиоматический подход!
Пример 1. Утверждается, что величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. Без намека на доказательство.
Пример 2. Описание установки мачты с помощью четырех растяжек и рисунок 96 неточные. Авторы думают, что каждая пара растяжек с мачтой лежат в одной плоскости, но не пишут об этом. По их тексту (и рис. 96) можно установить мачту не так, как хочется авторам. А они от этого примера приходят к утверждению, что мачта перпендикулярна любой прямой плоскости, дают определение перпендикуляра к плоскости, бездоказательно формулируют признак перпендикулярности прямой и плоскости и другие факты стереометрии.
Вы спросите, зачем? Ответим: авторы заботятся о пространственном воображении школьников — необходимом элементе их общекультурного развития. Но почему это надо делать в ущерб приучению детей к логике и к научной честности? Разве цели обучения математике так изменились, что теперь на уроке математики надо принимать сказанное на веру?
Прямо скажем, органичного включения стереометрии в курс планиметрии не получилось.
Одной из особенностей учебника И.Ф. Шарыгина является отказ от аксиоматического подхода. В нем уменьшена роль формально-логических рассуждений, больше внимания уделено методам решения задач. Наглядно-эмпирическое построение курса позволяет на раннем этапе обучения решать содержательные, интересные и красивые задачи.
Планиметрические задачи рассматриваются не только на плоскостных, но и на пространственных объектах. Это дает возможность не тормозить формирование пространственного (трехмерного) видения геометрических объектов, пространственного мышления школьников, а развивать их. Этому способствует продуманное использование наглядности в учебнике.
Интересен исторический аспект развития учебного материала, доказательства фактов, полученных великими математиками древности. Все это работает на воспитание интереса учащихся к предмету и уважения к классикам геометрии.
Учебник И.М. Смирновой и В.А. Смирнова следует традициям преподавания геометрии в школе, идущим от классических учебников А.П. Киселева. В нем реализован аксиоматический подход. Аксиомы вводятся постепенно по мере необходимости. Авторы используют избыточную систему аксиом, что в рамках первоначального изучения геометрии оправдано. Однако и здесь, как и в учебнике Погорелова надо следить за порядком вершин в обозначении треугольника.
В качестве дополнений к классическим вопросам планиметрии в учебнике содержатся материалы научно-популярного характера (графы, теорема Эйлера, проблема четырех красок и др.). Учебник завершается материалами по стереометрии, что позволяет распространить изученные понятия и свойства на случай пространства, готовить учащихся к изучению стереометрии в старших классах. В учебнике ощущается реальная забота о развитии пространственного воображения школьников — не в ущерб другим целям обучения математике.
Размещение упражнений непосредственно за учебным текстом улучшает ориентировку учителя и учащихся в учебнике, делает материал, связанный с данным учебным текстом, более обозримым.
Погорелов или атанасян что лучше
Сравнительный анализ школьных учебников геометрии
Шеховцова Дарья Николаевна,
аспирант Томского государственного педагогического университета.
Хорошо известно, что успехи в обучении школьников во многом зависят от содержания и структуры учебника, по которому они занимаются. По одним учебникам школьники работают с удовольствием (читают, рассматривают рисунки, активно выполняют предлагаемые задания). Другие учебные тексты воспринимаются иначе; видно, что большинство учеников с неохотой открывают учебник, находят нужный текст и равнодушно начинают работать с ним.
Чем же это обусловлено? Почему дети по-разному относятся к учебной книге? Оставим в стороне мастерство учителей и ту точку зрения, что хороший учитель может удачно провести урок, работая по любому учебнику. Попытаемся сравнить известные школьные учебники с позиций легкости восприятия и доступности усвоения учебного материала.
В современной школе наибольшее распространение получили учебники следующих авторов: Погорелов А.В., Гусев В.А., Александров А.Д. и др., Атанасян Л.С. и др., причем отмечается неоднозначное отношение учителей к этим учебникам. В методической литературе имеются и положительные и отрицательные отзывы о них; авторы одних статей считают, что некоторые учебники непригодны для современной школы, другие же, наоборот, восхищаются тем или иным подходом автора к изложению школьного курса геометрии [5, 6, 9]. Одних привлекает строгий аксиоматический подход, других большие возможности для организации мыслительной деятельности учащихся.
Чтобы сравнивать содержание разных учебников геометрии необходимо обратить внимание на то, какие цели обучения геометрии выбирались в качестве ведущих в последнее время. Сегодня основная цель обучения геометрии не связывается с развитием только логического мышления школьников [3]. Выделяют общекультурные, научные (собственно геометрические) и прикладные цели обучения геометрии [3, 10, 11]. Считается, что при обучении геометрии нужно стремиться к развитию у учащихся интуиции, образного (пространственного) и логического мышления, к формированию у них конструктивно-геометрических умений и навыков [3, 11].
Несомненно, реализация целей обучения геометрии в школе напрямую связана со структурой курса геометрии. Сегодня ведущие отечественные методисты и авторы учебников выделяют несколько этапов изучения школьного курса геометрии. Академик А.Д. Александров и профессор А.Л. Вернер преподавание геометрии в школе делят на три ступени. На первой ступени: 1-6 кл. геометрия выступает частью общего курса математики. В 7-9 кл. идет изложение систематического курса планиметрии, наполненного элементами стереометрии. А на третьей ступени, т.е. в 10-11кл. курс стереометрии ориентируется на классы с различной специализацией (гуманитарные, физико-математические и др.)
Школьная одежда оптом из Турции на opt-baby.ru
Другой педагог – Т. Ходот предлагает двукратное изучение курса геометрии: «один раз на интуитивном уровне и второй раз на строгом логическом». Изучение геометрии на наглядном, интуитивном уровне начинается в начальной школе, в процессе сюжетно дидактических игр. В 5-6 классах дети вовлекаются в конструирование и рисование знакомых геометрических фигур. Изучении планиметрии в 7-9 классах продолжается на стереометрическом материале, параллельно с соответствующим планиметрическим. В 10-11 классах ученики изучают стереометрию, изложенную аксиоматическим методом и дополненную разнообразными задачами, как планиметрическими, так и стереометрическими.
Безусловно, на каждой ступени обучения геометрии в школе важная роль в достижении намеченных целей обучения отводится используемым учебникам. При этом признается, что нужна хорошая учебная книга – учебник, который бы содержал необходимый минимум и материал для продвинутого обучения [4]. Причем большое значение имеет «внешняя оболочка» учебного материала, содержащегося в учебнике. Предлагаются разные способы управления познавательными действиями учащихся при работе с книгой, рассмотрим некоторые из них. Обратим внимание на вспомогательную знаковую систему учебников, т.е. на те значки, которые облегчают работу школьника при решении задач. Известно, что наличие разнообразных задач в учебниках, как варьирующихся по уровню сложности, так и творческих дает ученику свободу выбора и активизирует его стремление к знаниям. В качестве примеров рассмотрим учебник геометрии А.В. Погорелова, учебники авторских коллективов А.Д. Александрова и др. и Л.С. Атанасян и др.
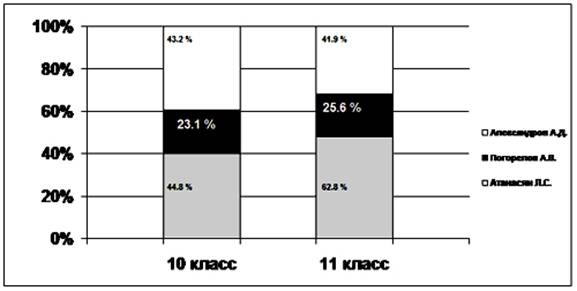
Представим информацию о количественном соотношении задач в учебниках геометрии для 10-11 классов в виде диаграммы (рис.1).
Среди основных положительных характеристик любого учебника выделяется развернутость текста учебника. Считается, что это заметно облегчает усвоение материала [8]. Если рассматривать учебник А.Д. Александрова и др., то следует отметить, что в этом учебнике к некоторым параграфам идут дополнения, позволяющие полнее раскрыть тему. Такое разграничение материала позволяет ученикам, прочитав параграф, не только уяснить его основные понятия, но и при желании, ознакомиться с дополнительной информацией по данной теме. Такое углубление знаний необходимо т.к. учебник изначально предназначен для учащихся школ и классов с физико-математическим профилем [1]. Учебники А.В. Погорелова и Л.С. Атанасяна и др., предназначены для общеобразовательной школы. Авторам приходится изучаемый материал излагать в краткой форме, учитывая, что он должен быть доступен для учеников с разным уровнем восприятия информации и подготовленности по предмету.
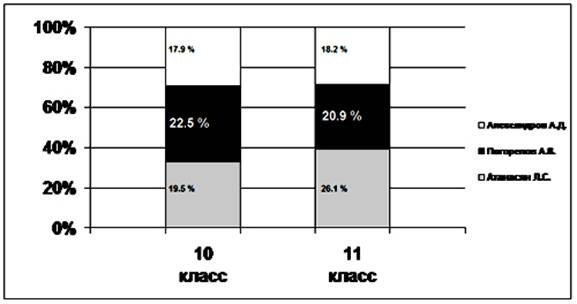
Эффективность обучения геометрии во многом определяется тем, каким образом кодируется информация, используются ли при этом рисунки, чертежи, схемы. Это объясняется тем, что геометрический метод и состоит в том, что само логическое доказательство или решение задачи направляется наглядным представлением; лучше всего, когда доказательство или решение видно из наглядной картины [4]. В последнее время специалисты все чаще говорят о необходимости визуализации геометрических связей в процессе формирования знаний школьников, и по-разному используют принцип наглядности при обучении геометрии. Академик А.Д. Александрова видит задачу преподавания в школе в единстве строгой логики и живого восприятия реального мира. В своем учебнике он предоставляет школьникам возможность самостоятельно обработать текстовую информацию, переводя ее на язык рисунков, схем, чертежей. Александров А.Д. считает: «Во всяком подлинно геометрическом предложении неразрывно присутствуют два элемента: наглядная картинка и строгая формулировка, строгий логический вывод» [1]. Поэтому количество рисунков в его учебнике не превосходит 19% от общего объема информации.
Авторский коллектив профессора Л.С. Атанасяна и др. – акцентирует свое внимание на развитии умений и навыков учащихся, на доступности изложения, считая, что каждый элемент курса геометрии должен опираться на возможно более простое и ясное наглядное представление [7]. Атанасян Л.С. включает в учебник большое количество рисунков и чертежей.
Проиллюстрируем на диаграммах соотношение визуальной информации, в рассматриваемых учебниках (рис.2).
3. Глейзер Г. Д. Каким быть школьному курсу геометрии //Математика. Приложение к газете «Первое сентября». 1990. №7. С.68-71.
4. Гусев В. А. Каким должен быть курс школьной геометрии?. //Математика. Приложение к газете «Первое сентября».2002. №3. С.4-8.
6. Маркова В. Формирование мышления учащихся. //Математика. Приложение к газете «Первое сентября».-2004.№34.
8. Мордкович А. Г. Каким быть школьному учебнику?. //Математика. Приложение к газете «Первое сентября». 2003. №8. С.2-5.
9. Феоктистова И.Е. Геометрия 7-11. //Математика в школе.- 2001. №5.
11. Школьная геометрия – реальность и перспектива//Математика в школе. 1999. №7. С.2-3.
Репетитор по математике о новом учебнике геометрии
Если заглянуть в любой книжный магазин, торгующий школьной литературой по математике, то сразу бросится в глаза одно обстоятельство: общее количество учебников по алгебре заметно больше числа аналогичных книжек по геометрии. До недавних пор на полке репетитора по математике лежали только два учебных монстра: геометрия (7 — 9 класс) Погорелова и Атанасяна, причем последний встречался примерно в 7 — 8 школах из 10. Объяснялось это обстоятельство жесткими логическими связями между темами, не позволяющими произвольно их переставлять.
Репетитор по математике о провале нового учебника геометрии
Не секрет, что механика всех строгих доказательств в геометрии основана на четкой логике использования теорем и аксиом. Это фундамент предмета, который нельзя разрушать. В начале курса техника доказательств отшлифовывается на признаках равенства треугольников (основа всех основ) на типичных для их работы темах: равнобедренный треугольник, параллельность, четырехугольники. Причем роль первой из них очень опасно недооценить. Однако, чтобы запустить признаки равенства треугольников, их для начала необходимо доказать. А вот тут и начинается самое интересное.
Систему точных аксиом Пеано в школе не дашь, поэтому Атанасян применяет свой собственный метод (правда весьма скользкий и тем самым опасный) – определять равенство треугольников через наложение. Что это за действо — объясняется весьма туманно и математически некорректно. Работать с ним невозможно, поэтому Атанасян крайне мало его эксплуатирует (только для вывода самих признаков), а дальше запускает признаки в оборот для обучения принципам / механике строгих геометрических доказательств. Активным помощником в этом процессе выступает тем: «равнобедренный треугольник».
Что мы видим в новом учебнике? Жуткое дело. Равнобедренный треугольник следует перед признаками. Когда я это увидел, то обомлел. Разыгралось любопытство: «А как же там строятся доказательства?» Открываю соответствующие параграфы и падаю на стул как подкошенный. Все факты объясняются через наложение. Мамочки родные! Это до какой степени деградации и неуважения к математике должен дойти автор, чтобы издавать подобную галиматью? Любой здравомыслящий репетитор по математике условно закидает автора помидорами. Читая учебник у ребенка может сформироваться неверное представление о том, что в главным инструментом изучения геометрии является наложение. Что увижу на рисунке, то и будет фактом. Наложу и все вам докажу. Ну куда это годится?
Не менее отвратным оказалась и дидактика. Задачи настолько усложнены, что даже взрослому человеку / репетитору по математике не сразу запомнить условие. Приходится по нескольку раз перечитывать, чтобы представить картинку. Моей ученице задали решить 4 последовательных номера. Первым же номером шла чрезмерно трудоемкая задача, состоящая из трех одинаковых выматывающих операций по поиску углов, а следом за ней точно такая же, но более простая на одну аналогичную операцию. Где же принцип поэтапного усложнения упражнений?
Тема параллельность вообще исключена из программы 7 класса, а вместо нее вставлена «Окружность». Причем изучаются вписанные углы, дуги, как в 8 классе. Ограничения по задачам к этим темам весьма существенные и учащийся просто не получит по ним нормальной практики.
Зачем портить хорошие учебники?
Современные издательства очевидно живут по законам рынка, а для него математика — всего лишь товар, средство для заработка. Магазинам нужен большой ассортимент книг, желательно с красивыми обложками и картинками, чтобы покупателю хотелось потратить на них свои кровные. Продавать одну и ту же позицию в течение 20 лет – скучно, долго и невыгодно. Атанасяном завалены все школы и полки всех репетиторов по математике. Нужен новый «бестселлер», пусть немного корявый, но зато свежий.
Ладно, с торговлей мне все уже давно ясно. Удивляет другое — позиция преподавателя математики, запустившего учебник Бутузова в работу. Неужели он не видел очевидных потерь в сравнении с Атанасяном? Может школу обязали? Но тогда позорно прогнило министерство образования. Самое интересное, что девочке выдали оба учебника, но почему то выбор пал на Бутузове. Тем временем, великолепный Атанасян лежит мертвым грузом. Ни одной задачи из него еще не было решено.
Репетитор по математике — практик со стажем, Колпаков А.Н. Москва, Строгино.
Добрый вечер, Александр!
Прочитала Вашу статью «Репетитор по математике о новом учебнике геометрии» и полностью с Вами согласна. У меня внук учится в 8 классе по Атанасяну и в ужас прихожу от учебников.
Иногда приходится помогать, но тогда захожу в интернет и ищу более понятное и грамотное разъяснение, трачу кучу времени. Потом обьясняю, чтобы дошло. У нас в советские времена был один учебник по алгебре и геометрии. Педагоги объясняли доходчиво, и я теперь еще что-то помню и могу объяснить. А сейчас ребенок решить ничего не может, входит в решебник и переписывает. Вот такие наступили коммерческие времена. Занимаемся с репетитором по математике через скайп (на что тоже Вы обращаете внимание). Учим геометрию и понимаю, что придется с этим заканчивать. Нет методики изучения материала и нет внятных разъяснений. Сама присутствую на занятиях, но не понимаю сути всего. Спасибо,что есть педагоги своего дела, обсуждающие горячие темы и провалы в нашем образовании.
Здравствуйте, Нина!
Сейчас в школьном образовании много посторонних субъектов, не имеющих к нему прямого отношение. В том числе и среди репетиторов по математике. Провозгласить себя частным преподавателем — дело одной регистрации на соответствующем сайте и при наличии умения решать задачки кажется, что больше ничего и не нужно. Однако кроме знаний предмета нужно понимать и уметь кое что еще. Да и не задачами едиными живет математика. Многие репетиторы сами порой не понимают, зачем человечеству, например, понадобились степени с иррациональными показателями, или почему «минус умножить на минус будет плюс». За долгую практику, а в последнее время все чаще, я сталкиваюсь со случаями невыразительного, а порой и вовсе криминального преподавания. На смену старой гвардии пришло целое поколение, одурманенное новыми программами и учебниками, без собственного уверенного понимания вопросов структурного построения и эволюции математики. Жаль.
Здравствуйте, Александр Николаевич!
Прочитала статью: действительно, у меня были похожие впечатления от этого трудного учебника. По нему учится один из моих учеников, причём он учится в сельской школе, где математика преподаётся по обычной, а не углублённой программе. Если честно, испытывала тихий ужас пока готовилась как репетитор к уроку геометрии: первые задачи после теории сразу даются на сложное доказательство, а некоторые номера я так и не смогла сделать, используя знания только 7-го класса. Думала, может, я просто чего-то не понимаю. Вспоминаю как сама училась по Погорелову, там, действительно, идут задачи от простых к сложным, и нас такой системой научили решать геометрические задачи. Сейчас все больше задумываюсь над методикой обучения у репетитора по математике, читаю Ваш сайт и понимаю, что передо мной ещё много-много материала. Были у нас в институте и технология обучения, и методика, но все равно кажется, что работаю недостаточно эффективно. Составляя программу занятий для отдельного ученика, каждый раз будто иду на риск: все ли верно методически? Пытаюсь проанализировать рабочие программы из Интернета. Подскажите, пожалуйста, методическое «чутьё» приходит только с опытом или может посоветуете литературу, чтобы повысить свою компетентность?
Здравствуйте, Юлия! Опыт, безусловно, главный подсказчик, необходимый репетитору по математике в повседневной работе. Нужно не только саму математику знать, но еще и программы / учебники нынешних и, что поважнее, ПРОШЛЫХ ЛЕТ. В них очень много правильного, в противовес современным «методикам заработка». Я уже лет 10 не смотрю в сторону методических пособий для преподавателей. Все лучшее и эффективное давно в голове. Вы тоже, я надеюсь, доведете до совершенства умение работать с учениками. А пока пробуйте разные объемы заданий, типы объяснений, формы работы и следите за реакцией детей, за их результатами. Основная проблема на практике состоит в том, что репетитор по математике зажат в тиски начальными условиями, на которые он не вправе повлиять. Кривые учебники — еще полбеды. Некоторые «продвинутые» умельцы — математики дают в рейтинговых школах свои программы. Да еще какие. Чуть ли не комплексные числа (в 8 классе. ) с выходом на формулы Кардано, мощность множества (в 7 классе 179 школе ей балуются), теория пределов с подробными доказательствами на языке эпсилон-дельта и т.д. Приходится распутывать клубки чужих методических просчетов «умных» дядек — профессоров. Никакие книжки не подскажут репетитору по математике как действовать в нестандартных условиях. Главное — знания на выходе из школы, а не то, какими путями они достигаются. Надо разговаривать с родителями и даже убеждать не зацикливаться на текущих оценках слепого следования дурацким программам. Но: любое отклонение (уход в сторону) с репетитором по математике дает дополнительную нагрузку ученику. Поэтому к вопросу неудачных программ надо подходить особенно взвешенно. И опять многое упирается в опыт.