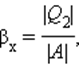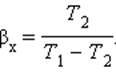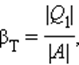Тепловая машина работает по циклу состоящему
Тепловая машина работает по циклу состоящему
С одним молем идеального одноатомного газа проводят циклический процесс 1-2-3-1, где 1-2 — адиабата, 2-3 — изобара, 3-1 — изохора. Температуры в точках 1, 2, 3 равны 600 К, 455 К и 300 К соответственно. Найдите КПД цикла.
КПД циклического процесса равно 
Найдем работу за цикл 
Для изохорного процесса 
При адиабатном процессе из первого закона термодинамики 
следует, что 
а изменение внутренней энергии 
Для изобарного процесса 
Учитывая, что из уравнения Клапейрона-Менделеева 
то 
Таким образом, работа газа за цикл
Из графика следует, что при изохорном процессе газ получал теплоту, при адиабатном процессе количество теплоты равно 0, при изобарном процессе газ теплоту отдавал. Значит, необходимо найти количество теплоты при изохорном процессе. Из первого закона термодинамики 
но при этом 
а 
то от нагревателя получена теплота 
Тепловой двигатель использует в качестве рабочего вещества 1 моль идеального одноатомного газа. Цикл работы двигателя изображён на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT12 к изменению его температуры ΔT34 при изохорном процессе равен 1,2. Определите КПД цикла.
КПД цикла равен 
Согласно первому началу термодинамики 
где 
(одноатомный газ).
В изобарном процессе 1–2 газ получает тепло, а его работа равна 
поэтому
В изохорном процессе 3–4 газ отдаёт тепло, а его работа равна нулю, поэтому
С учётом 
получаем
В таблице приведена зависимость КПД η идеального цикла Карно от температуры Tх его холодильника. Температура нагревателя поддерживается постоянной. На основании анализа этой таблицы выберите все верные утверждения.
| Tх, К | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
| η,% | 70 | 60 | 50 | 40 | 30 | 20 | 10 |
1) КПД цикла возрастает при увеличении температуры холодильника
2) Температура нагревателя равна 1000 К
3) Температура нагревателя равна 500 К
4) При температуре холодильника 0 °C данный цикл будет иметь КПД 100%
5) При температуре холодильника 650 К данный цикл будет иметь КПД 35%
Из таблицы видно, что при увеличении температуры холодильника, КПД уменьшается. 1 — неверно.
КПД тепловой машины может быть найден по формуле:
При температуре холодильника 
КПД тепловой машины будет меньше 100%. 4 — неверно.
При температуре холодильника 650 К данный цикл будет иметь КПД 
С идеальным одноатомным газом проводят циклический процесс 1-2-3-1. Найдите КПД цикла, если участок 12 — изохора, 23 — адиабата, 31 — изобара. T1 = 400 K, T2 = 600 K, T3 = 510 K.
Цикл не является циклом идеальной тепловой машины. Поэтому воспользуемся общей формулой через теплоту нагревателя и теплоту холодильника.
Необходимо выяснить, какой из участков цикла относится к нагревателю, а какой — к холодильнику. Для этого проведём подсчёт теплоты каждого участка по 1-му началу термодинамики: 
Работа равна нулю, так как это изохорный процесс. На нём нет изменения объёма. Теплота получилась на этом участке положительной. А значит, участок 1−2 вносит вклад в теплоту нагревателя.
2. На участке 2−3 представлена адиабата — по определению количество теплоты на этом участке равно нулю. Этот участок не учитывается при расчёте КПД по указанной формуле: 
3. На участке 3−1 представлен изобарный процесс. Тут нужно подсчитать и работу газа и внутреннюю энергию.
Количество теплоты тут получилось отрицательное — значит, этот участок соответствует теплоте холодильника.
4. Найдём значение КПД:
или примерно 8,3%.
Ответ: 
Аналоги к заданию № 11573: 11520 Все
В тепловом двигателе в качестве рабочего тела используется идеальный газ, а цикл состоит из двух изохор 1–2 и 3–4 и двух адиабат 2–3 и 4–1 (см. рисунок). Известно, что в адиабатических процессах температура газа изменяется в n = 2 раза (растёт в процессе 4–1 и падает в процессе 2–3). Найдите КПД цикла.
1. Работа газа за весь цикл равна, согласно первому началу термодинамики, суммарному количеству теплоты, полученной и отданной газом в цикле.
2. Газ получает теплоту на изохоре 1–2 в количестве
и отдаёт её на изохоре 3–4 в количестве
где CV — теплоёмкость данного количества газа при постоянном объёме.
3. Работа газа за цикл, таким образом, равна
4. КПД равен отношению работы к полученной теплоте:
С одним молем идеального одноатомного газа проводят циклический процесс 1−2−3−1, где 1−2 — адиабата, 2−3 — изобара, 3−1 — изохора. Температуры в точках 1, 2, 3 равны 600 К, 455 К и 300 К соответственно. Найдите КПД цикла.
Цикл не является циклом идеальной тепловой машины. Поэтому воспользуемся общей формулой через теплоту нагревателя и теплоту холодильника.
Необходимо выяснить, на каком из участков цикла газ получает тепло от нагревателя, а на каком — отдаёт холодильнику. Для этого проведём подсчёт теплоты каждого участка по 1-му началу термодинамики:
1. На участке 1−2 представлена адиабата — по определению количество теплоты на этом участке равно нулю: 
2. На участке 2−3 представлен изобарный процесс. Тут нужно подсчитать и работу газа и внутреннюю энергию.
Количество теплоты тут получилось отрицательное, значит, на этом участке газ отдаёт теплоту холодильнику.
3. На участке 3−1 объём газ постоянен, работа равна нулю:
Теплота получилась на этом участке положительной, а значит, газ получает теплоту от нагревателя:
4. Найдём значение КПД:
Ответ: 
Тепловой двигатель использует в качестве рабочего вещества 1 моль идеального одноатомного газа. Цикл работы двигателя изображён на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Зная, что КПД цикла равен 50%, определите модуль отношения изменения температуры газа при изобарном процессе ΔТ12 к изменению его температуры ΔТ34 при изохорном процессе.
При изобарном расширении на участке 1–2 газ получает от нагревателя количество теплоты Q12, а на участке 3–4 отдаёт холодильнику в изохорном процессе количество теплоты Q34. На других участках теплообмен отсутствует. В соответствии с первым началом термодинамики работа газа за цикл А равна разности количества теплоты, полученной от нагревателя и отданной холодильнику A = Q12 − Q34, а КПД теплового двигателя
Количество теплоты Q12, полученное при изобарном расширении на участке 1–2, равно сумме увеличения внутренней энергии газа при увеличении его температуры и работы газа этом участке: Q12 = ΔU12 + A12. Внутренняя энергия идеального газа пропорциональна абсолютной температуре, и для 1 моль одноатомного газа 
а её изменение
Работа газа при изобарном расширении A12 = p1(V2 − V1). Выражая её через изменение температуры с помощью уравнения Клапейрона — Менделеева pV = \upsilon RT, получим: A12 = p1(V2 − V1) = υ RΔT12.
Отсюда: 
Количество теплоты Q34, отданное при изохорном охлаждении на участке 3–4, равно уменьшению внутренней энергии газа этом участке:
В итоге получим: 
Отсюда находим: 
Ответ:
Идеальная тепловая машина работает с использованием цикла Карно. Температуру холодильника машины понижают, при этом температура нагревателя и количество теплоты, которое рабочее тело получает от нагревателя за один цикл, остаются неизменными. Как изменяются в результате этого КПД тепловой машины и совершаемая машиной за один цикл работа?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
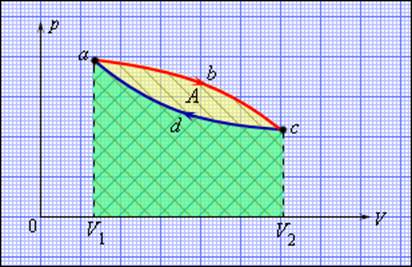
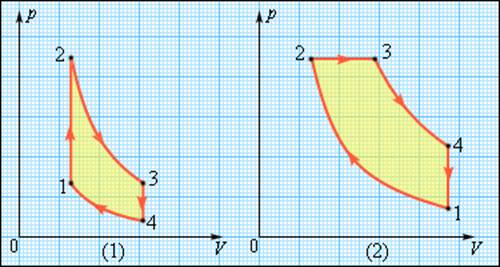
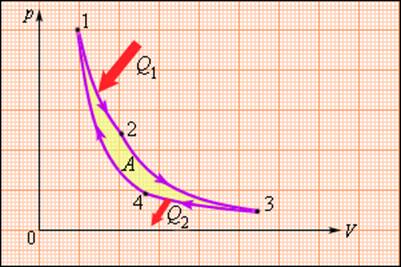
| КПД тепловой машины | Работа, совершаемая машиной Для КПД цикла Карно справедлива формула:
Отсюда видно, что при уменьшении температуры холодильника, КПД тепловой машины увеличится, а значит, увеличится полезная работа, совершаемая за один цикл. Цикл тепловой машины, рабочим веществом которой является ν молей идеального одноатомного газа, состоит из изотермического расширения, изохорного охлаждения и адиабатического сжатия. Работа, совершённая газом в изотермическом процессе, равна А, а КПД тепловой машины равен η. Максимальная температура в этом цикле равна Т0. Определите минимальную температуру Т в этом циклическом процессе. В данном цикле температуры Рассмотрим последовательно каждый процесс. Процесс 1−2: изотерма
Процесс 2−3: изохора
Процесс 3−1: адиабата
Полезная работа
Откуда Ответ: Тепловые двигатели. Термодинамические циклы. Цикл КарноТепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами. Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0): Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу A1, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A = A1 + A2 на диаграмме (p, V) равна площади цикла. Работа A положительна, если цикл обходится по часовой стрелке, и A отрицательна, если цикл обходится в противоположном направлении.
Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 0, A > 0, Q2 T2 В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.
Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2) В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 0, T1 > T2 Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q2| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением
т. е. эффективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении βх может быть и больше, и меньше единицы. Для обращенного цикла Карно
Если полезным эффектом является передача некоторого количества тепла |Q1| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность βТ теплового насоса может быть определена как отношение
т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует: следовательно, βТ всегда больше единицы. Для обращенного цикла Карно
|
и 
равны, температура 
меньше температуры 
так как на участке 2−3 происходит изохорное охлаждение. На участке 2−3 температура только уменьшается, а на участке 3−1 возрастает до значения 
следовательно, температура 
где 
— полезная работа, совершаемая тепловой машиной за цикл, 
— количество теплоты, переданное тепловой машине за весь цикл. Будем обозначать работу, теплоту и изменение внутренней энергии рабочего тела на каждом участке соответственно буквами 
и 
с соответствующими индексами. Обозначим разность температур 
как 
Также заметим, что разность 
отрицательна, поэтому 
равна площади, заключённой внутри цикла, 
Количество теплоты, переданное тепловой машине в цикле 
КПД тепловой машины будет равно
Значит, 
