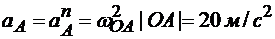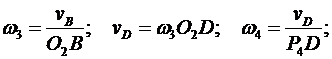Угловая скорость вращения колеса автомобиля вычисляется по формуле

Решение № 144 Угловая скорость вращения вала автомобильного двигателя ω(двиг) и угловая скорость вращения колёс автомобиля

Угловая скорость вращения вала автомобильного двигателя ω(двиг) и угловая скорость вращения колёс автомобиля ω(кол) измеряются в оборотах в минуту. Эти величины связаны соотношением:

где k – передаточное число дифференциала автомобиля, а b – передаточное число коробки передач при выбранной передаче. В таблице указаны передаточные числа для автомобиля «Лада-Калина».

Решение:

Сначала водитель ехал на 5-й передаче и непосредственно перед моментом переключения ω_двиг = 2000 ; k = 3,706; b₅ = 0,784. После переключения на вторую передачу параметр b₂ = 1,95. Учитывая, что скорость автомобиля оставалась прежней, угловая скорость колес оставалась постоянной. Получаем пропорцию:

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Источник

Равномерное движение тела по окружности

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ​ \( T \) ​ — время, в течение которого тело совершает один полный оборот. Единица периода — ​ \( [\,T\,] \) ​ = 1 с.

Связь между частотой и периодом обращения выражается формулой: ​ \( n=1/T \) ​.

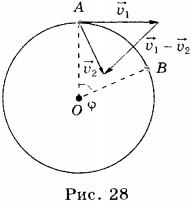
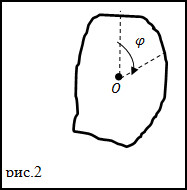
Пусть некоторое тело, движущееся по окружности, за время ​ \( t \) ​ переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ​ \( \varphi \) ​.

Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость ​ \( \omega \) ​ — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ​ \( \omega=\varphi/t \) ​. Единица угловой скорости — радиан в секунду, т.е. ​ \( [\,\omega\,] \) ​ = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ​ \( 2\pi \) ​. Поэтому ​ \( \omega=2\pi/T \) ​.

Линейная скорость тела ​ \( v \) ​ — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ​ \( \vec=l/t \) ​. За один оборот точка проходит путь, равный длине окружности. Поэтому ​ \( \vec=2\pi\!R/T \) ​. Связь между линейной и угловой скоростью выражается формулой: ​ \( v=\omega R \) ​.

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ​ \( \vec=\frac<\Delta\vec>\) ​ и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ​ \( a=\frac \) ​. Так как ​ \( v=\omega R \) ​, то ​ \( a=\omega^2R \) ​.

При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии ​ \( R_1 \) ​ от центра вращающегося колеса, равна ​ \( v_1 \) ​. Чему равна скорость ​ \( v_2 \) ​ точки 2, находящейся от центра на расстоянии ​ \( R_2=4R_1 \) ​?

1) ​ \( v_2=v_1 \) ​
2) ​ \( v_2=2v_1 \) ​
3) ​ \( v_2=0,25v_1 \) ​
4) ​ \( v_2=4v_1 \) ​

3. Период обращения точки по окружности можно вычислить по формуле:

1) ​ \( T=2\pi\!Rv \) ​
2) \( T=2\pi\!R/v \) ​
3) \( T=2\pi v \) ​
4) \( T=2\pi/v \) ​

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) ​ \( \omega=a^2R \) ​
2) \( \omega=vR^2 \) ​
3) \( \omega=vR \)
4) \( \omega=v/R \) ​

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) ​ \( 1/T \) ​
2) ​ \( v^2/R \) ​
3) ​ \( v/R \) ​
4) ​ \( \omega R \) ​
5) ​ \( 1/n \) ​

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

Источник

Угловая скорость.

Угловой скоростью называется величина, численно равная скорости точек, расположенных от оси на расстоянии единицы длины.

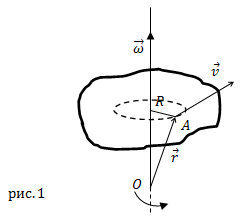
При вращении тела вокруг неподвижной оси АВ каждая точка тела М описывает окружность, перпендикулярную к оси, центр Р которой лежит на оси.

Скорость точки M направлена нормально к плоскости МАВ в сторону вращения. Равномерное вращение точки характеризуется постоянной угловой скоростью.

Угловой скоростью тела называют отношение угла поворота к интервалу времени, в течение которого совершен этот поворот. Если угловую скорость обозначить через w, то:

Угловая скорость выражается в радианах в секунду (рад/с).

При равномерном вращении, когда известна угловая скорость в начальный момент времени t₀ = 0, можно определить угол поворота тела за время t и тем самым положение точек тела:

За один период (промежуток времени Т, в течение которого тело совершает один оборот по окружности) угол поворота φ равен 2π рад: 2π = wT, откуда:

Связь угловой скорости с периодом Т и частотой вращения ν выражается соотношением:

А связь между линейной и угловой скоростями определяется соотношением:

Источник

Формула угловой скорости

Определение и формула угловой скорости

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($\bar<\omega>$ при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:

С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.

Формула, связывающая линейную и угловую скорости

Единицы измерения угловой скорости

Основной единицей измерения угловой скорости в системе СИ является: [$\omega$]=рад/с

Примеры решения задач

Решение. Для нахождения модуля угловой скорости применим формулу:

Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):

Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

Формула угловой скорости не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Скорости вращения тела заданы системой уравнений:

Модуль угловой скорости связан с углом поворота как:

Следовательно, угол поворота найдем как:

Источник

Угловая скорость вращения колеса

Центр колеса движется равно­мерно по прямой; следовательно, его ускорение т.е. центр колеса является мгно­венным центром ускорений.

Так как колесо вращается равномерно, то ускорения всех точек колеса равны центростремительным ускорениям этих точек в их вра­щательном движении вокруг мгновенного центра ускорения. Например, ускорения точек обода определяются так:

Ускорение каждой точки колеса направлено к мгновенному центру ускорений. В рассмотренном примере наглядно видно, что мгновенный центр скоростей Р и мгновенный центр ускорений Q являются раз­личными точками плоской фигуры. Мгновенный центр скоростей, не имея в данный момент скорости, имеет ускорение , а мгновенный центр ускорений, не имея в данный момент ускорения, имеет ско­рость .

С л у ч а й II. Известны модуль и направление ускорения какой-либо точки А плоской фигуры 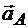, а также угловая скорость и угловое ускорение фигуры.

Определим положение мгновенного центра ускорений в частных случаях, зависящих от значений и .

1. Неравномерное вращение: . В этом случае мгновенный центр ускорений находится на отрезке, составляющем с направлением ускорения угол , который отложен от ускорения точки в сторону на расстоянии от точки А, равном

.

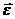
На рис. 12.13 показан случай ускоренного вращения плоской фигуры, а на рис. 12.14 — случай замедленного вращения.

Рис. 12.13 Рис. 12.14 Рис. 12.15

Ускорение любой другой точки плоской фигуры можно определить по формуле (12.4). Как видно, направление вращения на построение угла не влияет и угол всегда откладывается от направления ускорения в сторону .

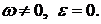
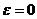
2. Равномерное вращение: (также момент, когда при неравномерном вращении) (рис. 12.15). В этом случае

и

т. е. ускорения всех точек направлены к мгновенному центру ускорений. Расстояние от точки до мгновенного центра ускорений определяется по формуле:

(12.6)

3. Момент, когда угловая скорость становится равна нулю: . В этом случае

т.е. ускорения всех точек направлены перпендикулярно отрезкам, соединяющим эти точки с мгновенным центром ускорений (рис. 12.16). Расстояние от точки до мгновенного центра ускорений определя­ется по формуле

(12.7)

Угловая скорость фигуры обычно обращается в нуль при измене­нии направления вращения фигуры.

4. Момент, когда угловая скорость и угловое ускорение становятся равными нулю при непоступательном движении: . В этом случае ускорения всех точек плоской фигуры в данный момент геометрически равны, так как ускорение любой точки равно ускорению полюса (рис. 12.17) по формулам :

.

С л у ч а й III. Известны модули и направления ускорений двух точек плоской фигуры. Допустим, что известны ускорения точек А и В плоской фигуры и (рис. 12.18).

Примем точку А за полюс, тогда

Построим при точке В параллелограмм ускорений по заданной диагонали и одной из сторон . Другая сторона параллелограмма определит ускорение во вращении точки В фигуры вокруг полюса А. Ускорение составляет угол с отрезком АВ, соединяющим точку В с полюсом А.

Отсчитывая полученный угол α от ускорения к отрезку АВ, получаем направление , в данном случае противоположное направле­нию вращения часовой стрелки. Определив угол α и направление , отложим этот угол от ускорений точек А и В по направлению . Две полученные полупрямые продолжим до пересечения в точке Q, которая и будет мгновенным центром ускорений.

Этот способ определения положения мгновенного центра ускорений не требует определения угла α путем вычислений. Если положение мгновенного центра ускорений по этому способу определяется графи­чески, то ускорения точек должны быть отложены в масштабе по их истинным направлениям.

Рассмотрим случаи, когда ускорения точек плоской фигуры парал­лельны. Положение мгновенного центра ускорений в этом случае определяется на основании того, что:

1) модули ускорений точек пропорциональны длинам отрезков, соединяющих точки с мгновенным центром ускорений:

.

2) ускорения точек составляют с отрезками, соединяющими точки с мгновенным центром ускорений, один и тот же угол .

На рис. 12.19 и 12.20 выполнено построение для случая , т. е. .

Рис. 12.21 и 12.22 соответствуют случаю α=90 о :

.

На рис. 12.23 и рис. 12.24 построен мгновенный центр ускорений для случая

Рис. 12.23 Рис. 12.24

.

В случае (рис. 12.23) мгновенный центр ускорений находится в бесконечности, а ускорения всех точек плоской фигуры геометри­чески равны.

Действительно, имеем

Пример 1. Колесо радиуса r = 1 м катится без скольжения уско­ренно по прямолинейному рельсу, имея в данный момент времени скорость центра v_o = 1 м/с и ускорение центра a_о — 1 м/с 2 (рис. 4.1.1). Определить угловую скорость и уг­ловое ускорение колеса, скорости и ускорения точек его обода М₁, М₂, М₃ и М₄, а также установить положение МЦС и МЦУ колеса.

Решение.

I. Определение скоростей. У колеса, катящегося без скольжения по неподвижной поверхности, МЦС (точка Р) находится в точке касания с этой поверхностью (рис. 4.1.2). В данном случае это точка M₁ (М₁ = Р): .

Для точек М₂ и М₃ расстояния до точки Р одинаковы, поэтому одинаковы и модули скоростей этих точек:

м/с.

Скорость точки М₃ м/с. Направления скоростей перпендикулярны отрезкам, со­единяющим точки с МЦС.

Для вычисления скоростей можно было использовать также и теорему о сложении скоростей, выбрав в качестве полюса центр колеса: , где v_MO = ω|МО|. Ско­рость перпендикулярна отрезку МО и направлена по ходу вращения.

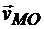
Можно было также пользоваться и следствием из этой теоремы о равенстве проекций скоростей точек на ось, проходящую через эти точки.

2. Определение ускорений. Вычислим сначала угловое ускорение колеса, формально дифференцируя выражение угловой скорости

.

В данном случае использован тот факт, что движение центра колеса прямолинейное и, следовательно, касатель­ное ускорение точки совпадает с полным ускоре­нием.

Для вычисления ускорений точек колеса применим теорему о сложении ускорений: , выбрав в качестве полюса центр колеса. Вращательное ускорение точки относительно полюса и направлено перпендикулярно отрезку МО по ходу угло­вого ускорения а центростремительное все­гда направлено от точки к полюсу.

Тогда для точек М₁, М₂, М₃ и М₄ получим , . Направления их показаны на рис. 4.1.3.

3. Определение положения МЦУ. Найти положение МЦУ (точки Q, ускорение которой равно нулю) можно на основании известных положений:

а) все ускорения составляют один и тот же угол β с направлениями из этих точек на МЦУ:

.

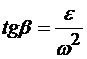
В данном случае tg β = 1 и β = 45°. Повернув каждое ускорение на угол β по ходу углового ускорения, мы на пересечении лучей и получим точку Q (рис. 4.1.4). Итак, МЦУ колеса при принятых исходных данных оказывает­ся на середине отрезка М₁M₄;

б) ускорения точек пропорциональны расстояниям от этих точек до МЦУ:

.

В силу одинаковости расстояний до МЦУ в данном слу­чае оказываются равны между собой модули ускорений , а также . Из всех точек колеса самое большое ускорение будет иметь точка D (рис. 4.1.4):

.

ω = 1 с –1 ; ε = 1 с –2 ; = 0; м/с; = 2 м/с; ; .

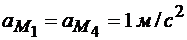
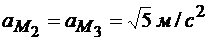
Пример 2. Кривошип OA длиной 0,2 м вращается рав­номерно с угловой скоростью ω_OA = 10 с –1 и при­водит в движение шатун АВ длиной 1 м. Пол­зун В движется по вертикали. Найти угловую скорость и угловое ускорение шатуна, а также скорость и ускорение ползуна в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с вертикалью угол 45° (рис. 4.1.5).

Решение.

1. Определение скоростей. Вычис­лим скорость точки А как точки вра­щающегося кривошипа:

.

Она направлена перпендикулярно ОА (рис. 4.1.6).

Скорость v_B ползуна направлена по направляющей вертикально.

Для шатуна АВ, совершающего плоское движение, теперь известны направления скоростей двух его то­чек: А и В. Восставляя перпендику­ляры к векторам этих скоростей, на­ходим точку Р их пересечения — МЦС шатуна.

Используя известную формулу для скоростей точек при плоском движении, получаем ; .

Из треугольника АВР имеем |АР| = 1 м; |ВР| = м, и тогда

.

2. Определение ускорений. Вычислим сначала ускоре­ние точки А как точки кривошипа: .

Здесь вращательное ускорение , так как , поскольку .

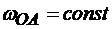
Тогда полное ускорение точки А равно центростремительному

и направлено к оси вращения — точке О (рис. 4.1.5).

Для вычисления ускорения точки В воспользуемся тео­ремой о сложении ускорений, взяв точку А в качестве полюса:

. (*)

Центростремительное ускорение точки В в относи­тельном вращении вокруг точки А по модулю равно , и направлено от точки В к полю­су — точке А.

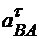
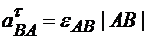
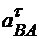
Модуль вращательного ускорения определяется по формуле и пока не может быть вычислен, поскольку неизвестна величина углового ускорения . Направление вектора также не может быть определе­но однозначно, так как неизвестно направление углового ускорения, т. е. неизвестно, ускоренным или замедлен­ным является поворот шатуна. Примем пока этот поворот ускоренным, тогда направление совпадет с направле­нием , а вектор направим перпендикулярно от­резку ВА по ходу углового ускорения.

Вектор ускорения точки В направлен по вертикальной прямолинейной направляющей. Будем пока считать дви­жение ползуна ускоренным и направим ускорение 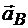в ту же сторону, что и скорость (рис. 4.1.6, 4.1.7).

Теперь в равенстве (*) все ускорения имеют определен­ное направление, и мы можем записать это уравнение в проекциях на выбранные оси:

.

Из последнего уравнения получаем , тогда из первого уравнения

.

Отсюда следует, что

.

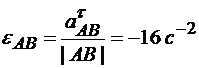
Отрицательные знаки у величин 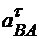и показывают, что их истинные направления противоположны принятым.

Пример 3. Круглый цилиндр А обмотан тонким тросом, конец которого В закреплен неподвижно. Цилиндр падает без начальной скорости, разматывая трос. Значение скорости оси цилиндра определяется формулой , где g – ускорение силы тяжести; у – расстояние, пройденное центром цилиндра, отсчитываемое от начального положения, т.е. координата точки А. Точка А движется прямолинейно по вертикали. Радиус цилиндра равен r. Определить скорости четырех точек на ободе цилиндра, расположенных на концах взаимно перпендикулярных диаметров, изображенных на рис. 4.1.8.

Решение. Мгновенный центр скоростей цилиндра находится в точке D, где неподвижная часть троса BD соприкасается с цилиндром. В этом месте скорости точек троса и цилиндра, находящихся в соприкосновении, равны между собой и, следовательно, равны нулю. Скорости остальных точек пропорциональны расстояниям до мгновенного центра скоростей и перпендикулярны к мгновенным радиусам. Величина скорости точки Е определяется из пропорции

,

откуда, учитывая формулу (1), находим, что

. (2)

Направление скорости точки Е перпендикулярно к мгновенному радиусу DE, т. е. параллельно скорости точки А. Скорости точек С и Н равны по величине, так как они отстоят от мгновенного центра скоростей, точки D, на одинаковых расстояниях DC=DH=r . Величины этих скоростей определяются из пропорции

,

, (3)

направлены эти скорости перпендикулярно к мгновенным радиусам CD и HD(рис. 4.1.8, б).

Формулы (2) и (3) определяют величину скоростей точек С,Е,Н как функцию пройденного центром цилиндра расстояния у. Найдем величину этих скоростей как функцию времени.

Так как точка А движется прямолинейно по вертикали, то

.

Отделяя переменные, имеем

Интегрируя это дифференциальное уравнение и полагая у=0 при t=0, находим уравнение движения центра цилиндра

.

Подставляя это значение расстояния у в формулы (2) и (3), получаем

Величину скорости точек С и Н можно также найти на основании теоремы о равенстве проекций скоростей двух точек плоской фигуры на прямую, соединяющую эти точки. Скорости точек С и Н составляют углы 45 о с линией САН, а скорости точки А направлена по этой прямой. Следовательно,

Пример 4. Прямоугольник ABCD совершает плоское движение. Ускорение точки А в данный момент равно =2 см/с 2 и составляет угол 30 о с прямой АВ. Ускорение точки В равно =6 см/с 2 и образует угол 60 о с прямой ВА. Длина сторон: АВ=10 см, ВС=5 см. Определить мгновенную угловую скорость и мгновенное угловое ускорение прямоугольника, а также ускорение точки С.

Решение. Выбираем точку А за полюс. Тогда ускорение точки В

. (1)

Проектируем векторное равенство (1) на оси х и у. В проекции на ось х имеем

Теперь найдем величину мгновенной угловой скорости фигуры

Проецируя векторное равенство (1) на ось у, получаем

.

Отсюда определяется вращательное ускорение точки В:

Далее находим величину мгновенного углового ускорения фигуры

.

Угловое ускорение фигуры направлено по оси z в отрицательную сторону.

Переходим к определению ускорения точки С. Согласно формуле распределения ускорений, выбирая точку В за полюс, имеем (рис. 4.1.9, б):

.

Проецируя это равенство на оси х и у, находим

Теперь легко найдется величина ускорения точки С:

.

Направление а_С определится формулами

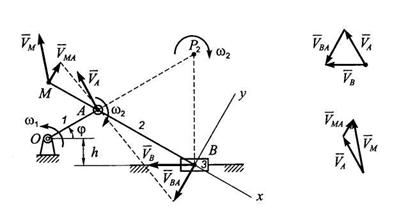
Пример 1.Кривошип ОА нецентрального кривошипно-шатунного механизма (рис. 8.2) вращается с угловой скоростью ω₁. Опре­делить скорости точек В и М, а также угловую скорость шатуна АВ для заданного положения звеньев механизма, если известно: φ =30°; ω₁ = 2 рад/с; ОА = 0,4 м; АВ = 0,8 м; АМ=0,4 м; h = 0,2 м.

Решение.Далее будут рассмотрены три способа решения задачи.

Разложим движение второго звена на переносное поступатель­ное и относительное вращательное. За полюс принимаем точку А и запишем теорему сложения скоростей для точки В.

.

Строим кинематическую схему механизма в выбранном масшта­бе (1:20), указываем на схеме направление скоростей точек A и В.

Зная угловую скорость кривошипа, найдем величину скоро­сти точки А

м/с.

Скорость направлена перпендикулярно прямой АВ, а пря­мая АВ образует с направлением скорости точки В угол 30° (так подобраны размеры звеньев), следовательно, скорость образует с горизонталью угол 60°, а скорость точки А перпендикулярна ОА (касательная перпендикулярна к радиусу) и образует с горизонта­лью также угол 60°.

Для определения скорости и скорости точки В построим в масштабе (1:40) треугольник скоростей (рис. 8.2 вверху справа).

На основании вышеизложенного этот треугольник равносторон­ний, следовательно,

.

Угловую скорость шатуна относительно полюса А находим по формуле

рад/с.

Заметим, что угловая скорость шатуна вокруг полюса равна аб­солютной угловой скорости.

Далее, зная угловую скорость шатуна, найдем скорость точки М в соответствии с теоремой сложения скоростей для этой точки

. (8.2)

Относительную скорость можно найти по формуле

,

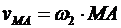
или графически, основываясь на том, что относительные скорости точек пропорциональны их расстояниям до полюса. Метод построе­ния ясен из рис. 8.2.

Из треугольника скоростей (см. рис. 8.2 внизу справа) с помо­щью измерений по масштабу находим

м/с.

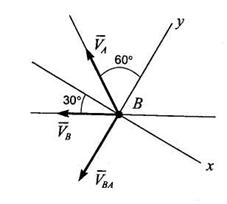
Задачу можно решить и без по­строения треугольника скоростей, на­пример, методом проекций. Найдем скорость точки В шатуна следующим образом: в точке В построим систему координат Вху (рис. 8.3), которая имеет­ся и на рис. 8.2. Изобразим векторы скоростей и и отметим величины углов (рис. 8.3). Далее, спроектируем векторное уравнение

.

Отсюда следует, что скорость точки В по величине равна скорости точки А. Если спроектировать указанное уравнение на вертикальную ось, то сразу определяется относительная скорость и, следова­тельно, угловая скорость шатуна. Эта операция предоставляется студенту для самостоятельного решения.

Тот же результат получится, если использовать теорему о про­екциях скоростей. Так как векторы скоростей точек А и В образуют один и тот же угол с прямой А В, то эти скорости равны по величине.

На рис. 8.4 изобразим в масштабе длин кинематиче­скую схему механизма и укажем мгновенный центр скоростей шатуна.

По построению треуголь­ник АР₂В равносторонний, следовательно, скорость точ­ки В равна скорости точки А. Угловая скорость шатуна

рад/с.

Скорость точки М равна

.

Расстояние Р₂М можно определить измерением или найти по из­вестной теореме косинусов

.

И тот, и другой метод дают одинаковый результат: Р₂М= 0,4 м. В соответствии с этим v_M = 0,4 м/с.

Заметим, что центры переносного, относительного и абсолют­ного вращений лежат на одной прямой и это есть общее правило. При этом угловые скорости переносного, относительного и пере­носного вращений связаны соотношением

.

При решении данной задачи перепишем эту формулу в таких обозначениях:

.

Заметим, что из всех угловых скоростей известна только угловая скорость кривошипа Ш\, которая для шатуна является переносной угловой скоростью.

Запишем теорему сложения скоростей для точки В

.

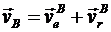
Переносная скорость точки В перпендикулярна прямой ОВ и ее величина определяется по формуле

.

Расстояние ОВ измеряем, или находим геометрически, исполь­зуя метрические соотношения в треугольнике ОАВ. В результате получаем ОВ = 1,06 м. Тогда переносная скорость равна 2,12 м/с. Относительная скорость направлена перпендикулярно АВ, а абсо­лютная скорость точки В направлена горизонтально. Этих данных достаточно для построения треугольника скоростей, который по­строен на рис. 8.5 вверху справа. Измеряя построенные векторы в выбранном масштабе, получаем

м/с; м/с.

Зная относительную скорость точки В, определяем угловую ско­рость шатуна в относительном вращении относительно кривошипа

рад/с.

По этой формуле определяется только абсолютная величина от­носительной угловой скорости. Изобразив вектор относительной скорости на кинематической схеме механизма (рис. 8.5), видим, что шатун вращается вокруг центра А по часовой стрелке. Это озна­чает, что относительная угловая скорость отрицательна.

Переходим к определению скорости точки М. Теорема сложения скоростей

.

Переносная скорость точки М направлена перпендикулярно прямой ОМ, относительная скорость направлена перпендикулярно прямой MB, а величины этих скоростей определяются по формулам

.

После вычислений находим м/с; м/с.

Строим треугольник скоростей (рис. 8.5 внизу справа), из кото­рого находим v_M = 1,06 м/с.

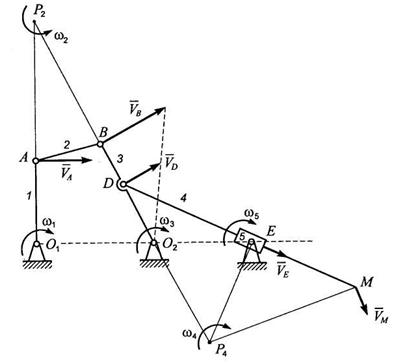
Пример 2.Механизм, изображенный на рис. 8.6, называется шарнирным четырехзвенником с присоединенной диадой. Звенья ме­ханизма имеют следующие размеры: О₁А = 0,3 м; АВ = 0,25 м; O₂D = 0,3 м; DB = 0,2 м; О₂Е=0,3 м; O₁O₂=0,6 м; DM=0,9 м; звено О₁А перпендикулярно О₁О₂. Кривошип О₁А вращается с угловой скоро­стью ω₁=4 рад/с по часовой стрелке. Необходимо определить угло­вые скорости всех звеньев механизма и скорости точек B,D, Е и М.

Решение.Механизм работает следующим образом. При враще­нии кривошипа О_ХА звено АВ совершает сложное плоскопараллель­ное движение, а второй кривошип О₂В вращательное движение, но при этом он не делает полного оборота, а совершает колебания от­носительно некоторого среднего положения. Звено DM при этом скользит поступательно вдоль цилиндра Е и одновременно с этим вращается вместе с цилиндром относительно оси его вращения.

Задачу будем решать в следующем порядке. Сначала найдем уг­ловые скорости всех звеньев и скорости заданных точек с помощью мгновенных центров скоростей. Затем найдем угловые скорости второго и третьего звена с помощью разложения движения второго звена на переносное поступательное и относительное вращательное. Далее, найдем угловые скорости четвертого и пятого звена и ско­рость точки М с помощью разложения движения четвертого звена на переносное вращательное и относительное поступательное. Затем найдем скорость точки М с использованием теоремы о скоростях и теоремы о проекциях скоростей.

Для выполнения намеченного плана изобразим в масштабе (1:10) кинематическую схему механизма, на которой построим МЦС звеньев и направления скоростей точек.

Мгновенные центры скоростей находим так. Совершенно оче­видно, что точка А движется по окружности радиуса О₁А, а точка В по окружности радиуса О₂В. Скорости точек А и В направлены по касательным к соответствующим окружностям. Следовательно, МЦС второго звена лежит на пересечении прямых О₁А и О₂В, т.е. в точке Р₂. Сложнее определить МЦС четвертого звена. Здесь сразу опреде­ляется только направление скорости точки D, так как ее траектория есть окружность с центром в точке О₂. На четвертом звене нет ника­кой другой точки, кроме точки D, для которой была бы известна траектория. Поэтому поступаем следующим образом. Разлагаем движение четвертого звена на переносное вращательное вместе с ци­линдром Е и относительное поступательное относительно цилиндра.

Далее, запишем теорему сложения скоростей для точки Е чет­вертого звена.

.

Заметим, что, согласно определению, переносная скорость точки Е четвертого звена равна абсолютной скорости точки Е пятого звена. Но эта скорость равна нулю, так как является для цилиндра Е центром вра­щения. Таким образом, абсолютная скорость точки Е четвертого звена равна относительной скорости, направление которой известно, так как в относительном движении четвертое звено движет­ся вдоль цилиндра прямолинейно. Дальнейшие построения понятны из рис. 8.7.

Далее, необходимо составить алгоритм для определения угло­вых скоростей звеньев и скоростей точек. Для этого предварительно найдем расстояния АР₂, ВР₂, P₄D, P₄E и Р₄М.

Измерения дают результаты:

Дальнейшие вычисления производим по формулам

После вычислений получаем ответ.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник