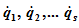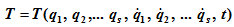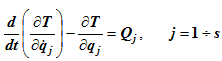Уравнение движения машины в форме лагранжа
Теоретическая механика. Уравнения Лагранжа
В этой статье мы попробуем разобраться с такой темой, как «Уравнения Лагранжа». Вообще, уравнения Лагранжа довольно полезная штука, например, на их основе решаются задачи на малые колебания. В МГТУ им. Баумана в третьем семестре предлагается самостоятельное домашнее задание, в котором нужно записать уравнения Лагранжа для системы с двумя степенями свободы.
Итак, типовое задание выглядит так.
Итак, приступим к решению.
Поскольку обобщенных координат две (две степени свободы), система уравнений Лагранжа будет выглядеть так:
С угловой скоростью катка тоже все понятно. Так как проскальзывание отсутствует
Векторно складываем эти две скорости
Определившись со скоростями, записываем выражение для кинетической энергии системы Т. Полная кинетическая энергия складывается из кинетических энергий всех тел, обладающих массой. То есть в нашем случае, тел 1, 3, 5.
Шарик 1 обладает энергией
Призма 3 движется поступательно
Каток 5 совершает плоское движение, так что его кинетическая энергия складывается из энергии поступательного и вращательного движений
Полная кинетическая энергия системы
Для записи уравнений Лагранжа это выражение нужно несколько раз продифференцировать.
Сначала по координате x. Частные производные
Производную по x с точкой дифференцируем по времени
Теперь то же самое по координате S. Частные производные
Производная по времени
Левая часть уравнений Лагранжа готова. Займемся правой частью. Для нее нужно посчитать обобщенные силы по каждой координате. Есть несколько способов это сделать, мы предпочитаем делать это через элементарную работу на малом приращении координаты. В общем случае формула выглядит так
На практике это применяется следующим образом. Сначала нанесем на рисунок все действующие силы. В нашем случае это сила упругости пружины и силы тяжести.
Сначала считаем обобщенную силу по координате x. Для этого мысленно «замораживаем» координату S, и позволяем системе свободно двигаться по координате x. То есть шарик «приклеивается» к пазу 2, и внутри него никуда не движется. Все перемещение происходит по координате x. Очевидно, что сила упругости работу не совершает, так как ее длина не меняется. Очевидно, что силы тяжести работу не совершают, так как движение происходит горизонтально. Официальным языком это записывается так
Теперь обобщенная сила по координате S. Мысленно «замораживаем» координату x. Получается, что призма 3 вместе с пазом 2 и катком 5 стоит на месте, а внутри неподвижного паза движется шарик. Сила упругости совершает работу, также как и сила тяжести шарика 1. Пружина была растянута на величину статической деформации δ и дополнительно растянута на S в произвольный момент времени, то есть сила упругости равна с·(δ+S). Работа силы упругости отрицательна, так как пружина растягивается. Работа силы тяжести шарика 1 положительна, так как шарик движется вниз. Силы тяжести призмы 3 и катка 5 работу не совершают, так как эти тела покоятся. Получаем
Собственно, все. Собираем все посчитанные величины в уравнения Лагранжа и получаем систему дифференциальных уравнений, описывающих движение системы.
Для проверки можно посмотреть размерности, в обеих частях выражения размерности должны совпадать (обычно это ньютоны).
Конечно, разные задачи немного отличаются в ходе решения, но алгоритм всех задач примерно такой.
1) Определить число степеней свободы и выбрать обобщенные координаты
2) Записать уравнения связей
3) Записать выражение для кинетической энергии
4) Взять необходимые производные
5) Записать обобщенные силы по каждой координате
6) Записать уравнения Лагранжа
Если что-то не получается, не отчаивайтесь, мы всегда рады помочь.
Уравнения движения в форме Лагранжа
Параметры времени Лагранжа
Чтобы получить уравнение движения гидромеханики исходя из точки Лагранжа, необходимо получить время и параметры как независимые переменные. Определяется начальное положение частиц жидкости в данный момент; все остальные величины, возникающие в уравнении движения, следует считать функцией аргумента.
Перейдите к общим уравнениям движения, замените их уравнениями движения в главе, а затем найдите должно быть выражено в последнем правиле. Умножив и сложив каждое из уравнений, мы попадаем в правую часть уравнения движения в форме Ламба. Точно так же после умножения и сложения, которое находится справа, и после умножения-сложение.
Получите сложение и достигните следующей Лагранжевой формы уравнения квантовая механика, есть также уравнения, которые характеризуют движение волновой функции, а также элементарные частицы в какой-то момент.
Установочная формула времени
Вы знаете все параметры (например, скорость и координаты), которые определяют состояние системы и их производные.Затем вы можете рассчитать эти параметры с первого раза за короткое время. Если выбрать небольшой, но конечный период времени, то можно оценить состояние системы в любой момент времени. To получив точное уравнение движения, нужно определить функцию, описывающую процесс.
Если выбрать достаточно малое время, то практически рассчитанные характеристики системы будут очень близки к этой функции.Законы движения классической механики определяют движение макроскопического материального тела и общая постановка задач гидродинамики, но, например, движение микроскопических частиц в Газе описывается с помощью статистических распределений.
Когда говорят об уравнениях движения в общеупотребительном смысле, подразумеваются дифференциальные или интегро-дифференциальные уравнения (хотя некоторые другие типы уравнений, например разностные — для дискретных систем — могут представлять собой достаточно близкую аналогию). Вики
Например, используя уравнение движения Больцмана, можно найти распределение плотности частиц в пространстве. Однако можно ли их назвать уравнением движения это в конце концов, квантовая система по своей сути неопределенна, а это означает, что невозможно получить точное решение уравнений движения.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
iSopromat.ru
Уравнения Лагранжа второго рода, которые представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат.
Для такой системы можно записать s уравнений, которые называются уравнениями Лагранжа второго рода или дифференциальными уравнениями движения в обобщенных координатах:
Уравнения Лагранжа второго рода могут быть обобщены на случай связей, осуществляемых с трением, хотя они и не являются идеальными. Для этого следует силу трения перенести из группы сил реакции в группу активных сил, тогда связь с трением можно формально считать идеальной.
Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения второго порядка относительно обобщенных координат q1, q2,…qs.
Дважды интегрируя эти уравнения и определяя по начальным условиям постоянные интегрирования, получим систему уравнений движения в обобщенных координатах:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Maple: составление уравнений Лагранжа 2 рода и метод избыточных координат
По роду профессиональной и научной деятельности я механик. Преподаю теоретическую механику в университете, пишу докторскую диссертацию в области динамики подвижного состава железных дорог. В общем, эта наука поглощает большую часть моего рабочего и даже свободного времени.
С Maple (на кафедре была 6-я версия, а у лоточников домой была куплена 8-я) познакомился ещё студентом, когда начинал работать над будущей кандидатской под крылом моего первого (ныше покойного) научного руководителя. Были и добрые люди, что помогли на самом первом этапе разобраться с пакетом и начать работать.
И вот так постепенно на его плечи была переложена большая часть вычислительной работы по подготовке диссертации. Диссертация была защищена, а Maple навсегда остался надёжным помошником в научном труде. Часто бывает необходимо быстро оценить какую-нибудь задачу, составить уравнения, исследовать их аналитически, быстро получить численное решение, построить графики. В этом отношении Maple просто незаменим для меня (ни в коем разе не хочу обидеть приверженцев других пакетов).
Сделать всё то, что будет предложено читателю под катом, меня подвигла задача принесенная ученицей (приходится ещё заниматься и репетиторством) со школьной олимпиады. Условие задачи таково:
Если не придираться к некоторонной туманности условия, то задача достаточно проста, а её решение, полученное путем довольно громоздких для школьника выкладок, в общем виде дает результат
И вот тут захотелось проверить решение, полученное с оглядкой на школьную программу по физике независимым способом, например составив дифференциальные уравнения движения этого маятника, да не просто, а с учетом освобождения от связи (в процессе движения нить, считаемая невесомой, провисает и маятник движется как свободная точка).
Это послужило катализатором для того, чтобы взять да и откопать свои старые задумки, накопленные ещё со времен работы в оргкомитете Всероссийской Олимпиады студентов по теоретической механике — три года подряд занимался там подготовкой задач компьютерного конкурса. Задумки касались автоматизации построения уравнений движений для механических систем с неудерживающими связями и трением, используя известные всем уравнения Лагранжа 2 рода
поборов стереотип многих преподавателей о том, что уравнения эти неприменимы к системам с неудерживающими связями и трением.
Что касается Maple, то его библиотека для решения задач вариационного исчисления дает возможность быстро получить уравнения Эйлера-Лагранжа, решение которых минимизирует действие по Гамильтону, что применимо для консервативных систем
где — функция Лагранжа, равная разности кинетической и потенциальной энергий системы.
Так как расматриваемые задачи не относятся к классу консервативных, то автором была предпринята попытка самостоятельно реализовать автоматизацию построения и анализа уравнений движений. Что из этого вышло, изложено под катом
1. Метод избыточных координат
Рассматриваем механическую систему, имеющую s степеней свободы, положение которой описывается вектором обобщенных координат . Пусть также имеется r неудерживающих связей, к числу реакций которых можно причислить и трение покоя, при превышении предельного значения переходящее в активную силу трения скольжения, направление которой противоположно направлению относительной скорости скольжения.
Учет неудерживающих связей требует от нас определения и анализа величины их реакций, поэтому необходимо так же определить их величину. Уберем указанные связи и введем дополнительно r обобщенных координат, выразив через них кинетическую энергию системы
Составим s + r уравнений движения в форме уравнений Лагранжа 2 рода
содержащие s+r неизвестных координат и r неизвестных реакций связей. Считая связи удерживающими, дополняем данную систему уравнениями связей (для простоты рассматривая геометрические связи) в виде
получаем замкнутую систему уравнений, из которой находятся значения реакций
являющиеся функциями первых s (независимых) обобщенных координат и скоростей и они могут быть расчитаны на любом шаге интегрирования уравнений движения (1). Для удерживающих связей типа «нить/поверхность» уравнения (1) и (2) надо дополнить условием освобождения от связи
а для связей с сухим трением вида
где Fj и Nj соответственно касательная и нормальная составляющая реакции; vj — проекция скорости относительного проскальзывани точки приложения реакции.
Таким образом, уравнения (1) — (4) представляют собой полную математическую модель движения рассматриваемой механической системы.
Засим с теорией можно покончить и перейти к практике
2. Maple-функции построения и анализа уравнений Лагранжа
Для решения этой задачи была написана Maple-библиотека lagrange, содержащая четыре функции
LagrangeEQs — построение уравнений движения в форме Лагранжа 2 рода
В качестве входных параметров функция принимает выражение кинетической энергии T как функцию обобщенных координат и обобщенных скоростей; массив обобщенных координат q; массив радиус-векторов точек приложения сил r и массив векторов сил F.
LinksEQs — получение уравнений дифференциальных связей из уравнений геометрических связей
Здесь надо отметить, что система уравнений геометрических связей eqs должна содержать избыточные координаты в явном виде, то есть иметь вид
в противном случае функции библиотеки не смогут обработать уравнения правильно. Для тестирования возможностей библиотеки сойдет и так, но в дальнейшем этот момент будет переработан: просто пока неясно, будет ли гарантированно разрешена система уравнений связи относительно угловых избыточных координат.
ReduceSystem — преобразование уравнений движения с учетом уравнений связей
Данный код в подробных пояснениях не нуждается — тут выполняется подстановка избыточных обобщенных координат, скоростей и ускорений, выражаемых уравнениями геометрических и дифференциальных связей в уравнения движения, с целью приведения их к виду, пригодному для вычисления реакций неудерживающих связей
SolveAccelsReacts — решение уравнений движения относительно реакций и обобщенных ускорений
Данная функция принимает на вход систему уравнений движения eqs, преобразованную с учетом уравнений связей. Она линейна относительно вторых производных независимых координат и реакций связей. Другие входные параметры: q — вектор независимых координат; R — массив реакций, относительно которых необходимо разрешить уравнения движения.
Теперь проиллюстрируем, как применять описанное «хозяйство» в деле
3. Задача о маятнике на тонкой нерастяжимой нити
Расчетная схема будет такой. В качестве обобщенной координаты выбираем угол наклона нити к вертикали.
Поскольку нить — неудерживающая связь, нас будет интересовать её реакция, а значит введем дополнительную, избыточную координату r(t).
Приступаем. Чистим память и подключаем библиотеку линейной алгебры
Подключаем библиотеку lagrange
Определяем вектор обобщенных координат, вычисляем координаты и скорость груза, а так же кинетическую энергию системы
На выходе получаем выражение для кинетической энергии (для вставки сюда использована функция latex(), генерирующая результат в LaTeX-нотации)
Формируем массив сил и массив координат точек их приложения
Скармливаем всё функции LagrangeEQs()
получая на выходе уравнения движения
Нетрудно убедится, что функция отработала нормально — для иллюстрации специально выбрана не слишком громоздкая задача.
Далее задаем уравнение связи — пока нить натянута, справедливо условие
преобразуем систему с учетом этого условия и находим реакцию связи
Сила натяжения нити равна
Система (5) — (7) является полной системой уравнений движения груза, с учетом возможности провисания нити. Теперь подготовим её к численному интегрированию. Для начала разрешим её относительно ускорений, передав в SolveAccelsReacts() уравнения (5) и (6), вектор обобщенных координат и пустой массив реакций
Для численного моделирования, хоть это и не спортивно, напишем отдельный код, дабы не забивать голову читателя длительной обработкой полученной системы напильником. Тем более что моделирование будет иметь свои особенности.
Готовим исходные данные и систему уравнений движения
Строим функцию вычисления состояния системы, при заданной горизонтальной начальной скорости груза
Теперь проверяем «школьное» решение задачи
В итоге, получаем результат, приведенный на скриншоте. Скорость груза в момент удара соответствует приведенному в предисловии значению, и видно, что до провисания нити груз движется по окружности, а после провисания нити движется как свободная точка под действием силы тяжести, по параболе.
Замечу, что погрешности попадания в гвоздь — вынужденная мера: в полярных координатах, которые были использованы, задача имеет особенность, понятную из уравнения (8). Поэтому r(t) сравнивалось не с нулем, а с величиной eps достаточно малой, чтобы получить решение, и достаточно большой, чтобы численный решатель fsolve() не сходил с ума. Однако это нисколько не умаляет практической ценности изложенных результатов.
Вместо заключения
Возможно, читатель упрекнет меня, что я стреляю из пушки по воробьям. Однако, хочется заметить, что всё сложное начинается с простого, а большая наука — с малых задач.
Тестовую версию библиотеки можно качнуть тут
Формализм Лагранжа в задачах с сухим трением
Тонкий однородный стержень массы m = 2 кг, длины AB = 2l = 1 м в точке A шарнирно прикреплен к невесомому ползуну, перемещающемуся в горизонтальных шероховатых направляющих. В начальный момент времени стержень расположен вертикально, затем его отклоняют от вертикали на ничтожно малый угол и отпускают без начальной скорости. Необходимо составить уравнения движения данной механической системы и найти закон её движения. Коэффициент трения между ползуном и направляющими равен f = 0,1.
Прежде чем приступить к решению задачи предлагаемым автором методом, рассмотрим немножко элементарной теории, касающейся сухого трения.
1. Что может быть «проще» трения?
Нет более страшного наказания для механика, чем сила трения. Появляясь в задаче, эта сила сразу делает её существенно нелинейной, ибо ведет себя достаточно интересным образом.
Рассмотрим довольно простой пример. Пусть на шероховатой поверхности покоится горизонтальный брусок.
Пусть в начале к нему не прилагают никаких сил (кроме силы тяжести и нормальной реакции). В этом случае и сила трения между бруском и плоскостью будет равна нулю.
Теперь приложим к бруску небольшую горизонтальную силу. Брусок не сдвинется с места, так как в ответ на наше воздействие со стороны поверхности на него станет действовать сила трения, которая будет удовлетворять условию
Будем постепенно увеличивать силу и, согласно (1) расти будет и сила трения, которая в этом случае называется силой трения покоя. Так будет продолжаться до тех пор, пока сила трения покоя не достигнет величины
называемой предельной величиной силы трения покоя. Здесь f — коэффициент сухого трения между бруском и плоскостью; N — нормальная реакция со стороны плоскости. После этого сила трения расти перестанет, а при дальнейшем увеличении горизонтальной силы начнется скольжение бруска. Сила трения перейдет в силу трения скольжения, равную
где — скорость бруска.
Пример весьма тривиальный, однако он раскрывает суть поведения силы сухого трения. Таким образом, получаем следующий алгоритм расчета силы трения:
2. Моделирование движения системы с трением
Теперь решим нашу задачу. Рассматриваемая нами система имеет две степени свободы, однако из-за необходимости определения нормальной реакции расширяем число степеней свободы до трех и получаем следующую расчетную схему
Здесь в качестве обобщенных координат берем вектор
где x,y — координаты точки A; — угол наклона стержня к вертикали. Вооружаемся Maple’ом
Определяемся с кинематикой системы
Вычисляем её кинетическую энергию
Maple выдает такой результат
Довольно громоздко, но «ковырять» нам не руками на листочке, поэтому двигаемся дальше. Задаем векторы и точки приложения сил
Получаем уравнения движения системы в форме Лагранжа 2 рода
Получаем трёх «крокодилов»
Эти уравнения пришлось вбить в статью руками, ибо «копипаста» LaTeX-вывода Maple приводит к неприглядному виду результата. Но даже так видно — уравнения сложны и с учетом того что F — это сила трения, аналитически не интегрируемы.
Теперь введем уравнения связей. Во-первых, ползун движется по горизонтальным направляющим, поэтому
Кроме того, в том случае когда ползун неподвижен, а сила трения покоя не превысила предельного значения, включается ещё одна связь
где — некоторая горизонтальная координата ползуна. Теперь преобразуем систему (4) — (6) с учетом уравнений (7) и (8) и найдем силу трения покоя и нормальную реакцию
Тут приведу результат непосредственно выданный Maple
Если посмотреть на полученные выражения, то они вполне соответствуют логике процесса. Теперь получим выражение для расчета нормальной реакции в случае, когда ползун скользит по направляющим, учитывая, что в этом случае сила трения будет определятся выражением
(минус уже имеется в уравнениях движения)
М-да, «крокодилище» вышел ещё тот, особенно с учетом что Maple таки довольно избыточно генерирует LaTeX-код
Все необходимые нам выражения получены, теперь можно переходить к моделированию. В отличие от задачи с маятником, о которой я уже писал, тут мы честно трансформируем наши уравнения Maple-средствами для вида пригодного к численному решению. Прежде всего решим уравнения (4) — (6) относительно обобщенных ускорений
Результат уже не буду приводить — он тоже довольно громоздкий. Перейдем к фазовым координатам
Формируем функции вычисления необходимых нам сил
Приведенный код хоть и объемный, но довольно прост — выполняется подстановка численных параметров в соответствующие выражения и их вычисление. Такую же функцию формируем и для вычисления обобщенных ускорений
Задаем параметры, данные нам в условии задачи
Время задать основную логику модели, которая определяет расчет силы трения. При этом задаемся погрешностью скорости ползуна, при которой будем считать её равной нулю.
Определяем callback для решателя:
Формируем для решателя список фазовых координат и начальные условия (угол отклонения стержня от вертикали делаем малым) и выполняем численное интегрирование (на самом деле последний вызов dsolve() лишь обозначает наши намерения по численному решению — оно будет поизведено при вычислении конкретных значений фазовых координат).
Выполняем некоторые подготовительные операции
Далее просчитаем движение системы в течение некоторого интервала времени и сформируем массивы данных для вывода на графики
Ну вот, у нас практически всё готово
Получаем графики. Красоты ради, графики были конвертированы из Maple в *.eps и немножко обработаны в inkscape.
Перемещение ползуна
Угол отклонения стержня от вертикали
Сила трения
Здесь синей линией показано предельное значение трения покоя, а красной — фактическое значение силы трения.
Нормальная реакция со стороны направляющих
Видно, что ползун покоится в течение чуть более двух секунд, а затем, после преодоления трения покоя приходит в движение, которое постепенно затухает и полностью прекращается через 6,5 секунд после начала движения. После этого сила трения никогда не превышает предельного для покоя значения, ползун остается на месте, а стержень совершает гармонические колебания около устойчивого положения равновесия.
Заключение
Рассмотрено применение метода избыточных координат и уравнений Лагранжа 2 рода к анализу движения систем с сухим трением. Видно, что при внешней громоздкости получаемых результатов, процес синтеза уравнений движения может быть автоматизирован средствами символьной математики, а это существенно для современных технических задач.