Что такое пузырек в физике
Физика пузырьков: поиск механизма разрушения пены
Самые простые вещи могут иметь самые необычные и даже неизученные аспекты. С малых лет мы пытаемся понять естество всего, что нас окружает. Как работает лампочка в люстре, почему небо синее, откуда дождь идет, почему лимон кислый, а сахар сладкий — это лишь малый список вопросов, которые может задать любопытный ребенок за очень малый промежуток времени. Вырастая, мы не так сильно интересуемся подобными вещами, уделяя внимание чему-то более важному, по нашему мнению. Но понимание природы простых, на первый взгляд, вещей может иметь большую пользу.
Сегодня мы познакомимся с весьма необычным исследованием, в котором ученые пытались понять механизм разрушения пены. Вы когда-нибудь задумывались, почему пенка в вашем капучино не такая долговечная, как хотелось бы? Если вам говорили, что вы просто не умеете ее готовить, то теперь у вас будет весьма научный контраргумент. Какая именно череда событий приводит к разрушению структуры пены, что является катализатором этого процесса и какая польза от таких знаний? Ответы на эти и другие вопросы мы найдем в докладе исследовательской группы. Поехали.
Основа исследования
Какой бы простой на первый взгляд не казалась пена, она все же остается сложной системой с газовой дисперсной фазой и жидкой/твердой дисперсионной средой. Если говорить о самой распространенной пене, состоящей из пузырьков газа и жидких пленок, то такая структура считается неравновесной системой. Также пену можно назвать и полидисперсной системой из-за того, что составные пузырьки могут быть совершенно разного размера. Кроме того, пена является очень неустойчивой и от того очень недолговечной системой ввиду того, что плотность жидкости в сотни и даже тысячи раз превышает плотность газа.
Несмотря на это пены достаточно распространены в жизни человека и применяются в самых разных сферах. Они присутствуют в повседневной жизни (взбитые сливки, пена для бритья и т.д.), в биотехнологиях (пены в биореакторах), в химических технологиях (пенная флотация) и даже в фармакологии. Если же изучить механизм, скрывающийся за процессом разрушения пены, то можно сделать ее более долговечной, как заявляют сами исследователи.
В своем труде они указывают на три основных процесса, регулирующих динамику пены: укрупнение, осушение и разрушение. Укрупнение — это процесс уменьшения числа пузырьков, но увеличение их размера, что вызвано разным давлением между пузырьками. Осушение — это процесс утончения пленок, то есть стенок пузырьков, за счет стока воды под воздействием гравитации.
Эти два этапа жизни пены ранее уже были достаточно хорошо изучены, как, в общем, и процесс разрушения. Предыдущие исследования показали, что разрушение пузырька происходит при достижении нижнего предела коалесценции* в объемной доле жидкости
Коалесценция* — слияние частиц внутри подвижной среды (например, пузырьков в пене).
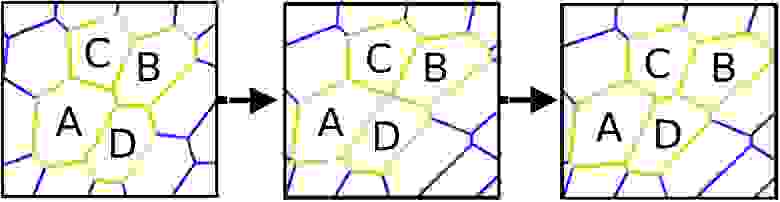
Процесс Т1* или перегруппировка Т1* — процесс изменения формы клеточных материалов (пена, биологические ткани и т.д.), состоящих из капель, пузырьков, клеток.
В начале процесса имеется 4 объекта (А, B, C и D). А и B контактируют, C и D расположены по обе стороны от АB, то есть не контактируют между собой. Разрыв связи между А и B с последующим установлением связи между C и D — это и есть процесс Т1.
В момент разрушения пузырька можно было услышать легкий «хлопок» (высвобождение газа). Измерив и проанализировав акустические данные в момент разрушения пены, ученые пришли к выводу, что этот процесс возникает из-за коллективного коллапса пузырьков (ККП), другими словами каскадного коллапса.
Но ККП является лишь верхушкой айсберга, а сам механизм, запускающий его в действие, неизвестен. Это как понимать, что цепочка домино разрушается, потому что доминошки падают друг на друга, но не знать какая из них была первой и что ее опрокинуло (грубоватая, но понятная аллегория).
В данном труде ученые использовали в качестве «подопытного» квазидвумерную пену, на краю которой лопается 1 пузырек. Каскад разрушения всей пены ученые наблюдали с помощью высокоскоростной камеры, после чего провели анализ записей. Было установлено два механизма распространения коллапса: распространение и проникновение.
По мере увеличения φ (объёмной доли), капелькам жидкости становится все труднее проникать сквозь жидкие пленки, что приводит к отскоку каплей от пленок из-за их упругости или поглощение капель пленкой. Более подробно об этом в результатах наблюдений.
Результаты исследования
Процесс ККП (коллективного коллапса пузырьков) наблюдался при разных значениях φ. Так, к примеру, на изображении 1а показан ККП от времени t = 0 мс до 3,12 мс для φ = 0,0099.
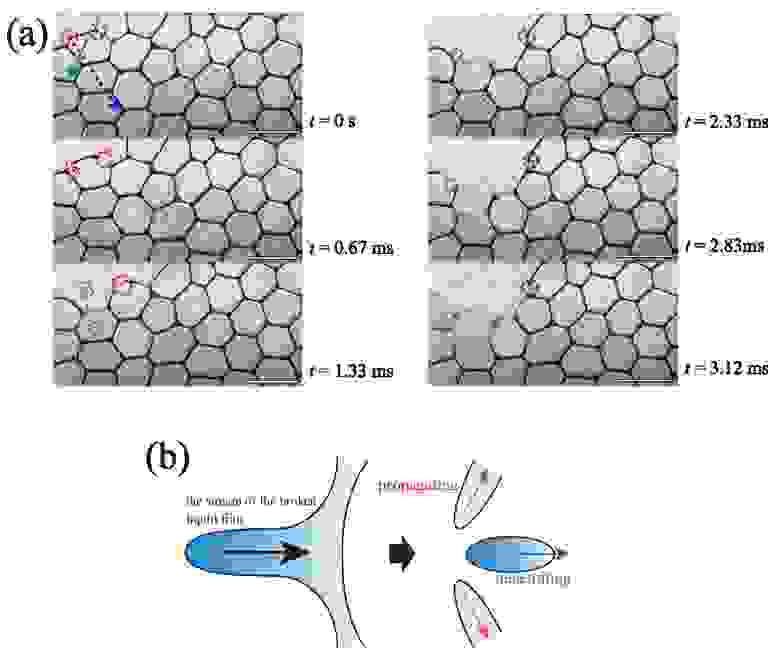
Изображение №1

Процесс ККП (t = 0 … 3,12 мс, φ = 0,0099).
Для прокола пузырька использовалась капиллярная стеклянная игла. Коллапс пузырьков в начале процесса ККП наблюдается по внешним краям пены, что ученые решили назвать поверхностным эффектом. Следом за этим начинаются два процесса ККП внутри самой пены, так сказать в ее общем объеме: распространение и проникновение.
Когда жидкая пленка разрывается, она быстро поглощается каналом Плато.
По закону Плато ребрами пузырька в пене являются каналы, заполненные дисперсионной средой. В одном канале могут сходиться только три пленки, расположенные под углами 120°.

Строение ячейки (пузырька) пены.
Из-за сильного поглощающего воздействия следующая жидкая пленка, сходящаяся в том же канале Плато, также разрывается (красный круг на 1а). Этот последовательный (каскадный) процесс разрушения пузырьков пены и является одним из процессов ККП — распространение (1b).
Одновременно с этим в момент поглощения каналом Плато лопнувшей пленки выделяется капля жидкости (синий и зеленый круги на 1а). Капли попадают внутрь пены в удаленную жидкостью пленку (стрелки на 1а). Скорость этих капель (Vd) составляла примерно 3 м/с. Этот процесс ККП, именуемый проникновением, приводит к разрушению удаленных пленок (1b).
Полный коллапс происходит при многогранных разрушениях пленок пузырьков через оба варианта ККП.
Если же увеличить φ до ≥ 0,015, то вероятность возникновения капли жидкости в момент разрушения пленки пузырька сильно снижается. И скорость все же возникших капель также становится меньше, от чего каплям становится труднее проникнуть в удаленные пленки. Вместо проникновения происходит отскок капли.

Отскок капли (вместо проникновения) при φ ≥ 0,015.

Изображение №2
На изображении выше показано как капля отскакивает от пленок в течение 30 мс (пунктирная линия это траектория движения капли).
Измерив скорости капли (Vd) после каждого отскока, можно построить график зависимости Vd от числа ударов (ni).

Изображение №3: зависимость скорости от числа отскоков.
Как и ожидалось, скорость капли уменьшается с увеличением числа отскоков. В таком случае можно определить коэффициент восстановления пленки как e = |Vd(i + 1)| / |Vd(i)|, где |Vd(i)| — скорость капли после i-го отскока. Используя данные наблюдений, было установлено, что е = 0,50
0,74. После i-го отскока капля впитывается жидкой пленкой.
При дальнейшем увеличении φ (> 0.022) пленка успешно поглощается каналом Плато, но жидкие капли не возникают. Пузырьки по краю пены лопаются от поверхностного эффекта и при более высоких показателях φ, но число таких пузырьков сильно снижается, а сам процесс коллапса быстро останавливается. Другими словами, процесс ККП не возникает.
Далее ученые исследовали зависимость числа лопающихся пузырьков от показателя φ. Совокупность разрушающихся пузырьков (Ntotal) состоит из тех, что лопаются на краю пены из-за поверхностного эффекта, и тех, что разрушаются за счет проникновения и распространения.
Также в расчетах применяется показатель Ninner — число разрушающихся пузырьков в объеме пены за вычетом внешних краев. Подсчет разрушающихся пузырьков осуществлялся от первого и до последнего пузырька, что заняло примерно 0.04 секунды.

Изображение №4
На изображении выше показаны значения Ntotal (красный цвет) и Ninner (синий цвет) относительно φ. Треугольники, кружки и квадраты соответствуют Ntotal или Ninner при Nf
200 для концентраций глицерина 9,4%, 17,8% и 29% соответственно (Nf — общее число пузырьков в пене).
Как мы видим из графика, значение Ntotal и Ninner уменьшается при увеличении φ. Применив степенной закон*, ученые установили, что Ninner ∝ φ −γe при γe = 2,3 ± 0,36.
Степенной закон* — функциональная зависимость двух величин, когда изменение одной приводит к пропорциональному изменению другой.
Также было установлено, что показатели Ntotal и Ninner не зависят от концентрации глицерина, если она ниже 29%. Если же концентрация увеличивается до 40%, то проколоть пузырек становится сложнее, а процесс ККП не возникает.
Исследование разрушающихся пузырьков в случае более крупной пены (Nf
500) показало, что их число не зависит от общего числа пузырьков (ромбы на графике выше), то есть Ntotal и Ninner не зависят от Nf.
Как мы помним, для прокола использовалась стеклянная игла. Она была покрыта силиконовой смазкой для улучшения прокалывания. Ученые проверили как это влияет на значение Ntotal и Ninner, совершив проколы без смазки. Таким образом процесс ККП возникал спонтанно. Однако, как и следовало ожидать, использование смазки никак не повлияло на число коллапсирующих пузырьков и на процесс ККП в целом.
Если же φ мало, то форма каждого пузырька анизотропная, и искаженные пузырьки формируют некое подобие цепочки. Пузырьки анизотропной формы и/или большого размера имеют большую избыточную поверхностную энергию, следовательно, они легче разрушаются.
Учитывая это, ученые решили проверить взаимосвязь ККП и формы пузырьков. Для этого был использован параметр λi как характеристика анизотропии пузырька i. λi определяется по следующей формуле:
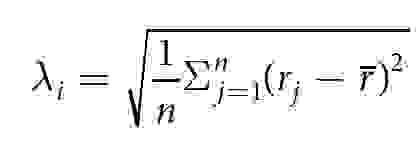
где j — пиксель на краю пузырька, n — общее число пикселей j, rj — расстояние между центром пузырька i и пикселем j, r — среднее расстояние rj.
λi будет равна 0, если пузырек i круглой формы. Если же он анизотропный, то λi > 0.
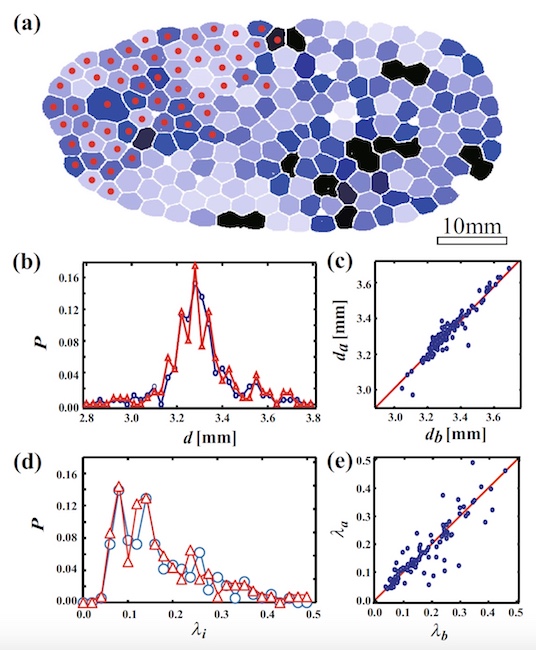
Изображение №5
На изображении 5а показана пена при φ = 0.0086 до начала процесса ККП. Пузырьки окрашиваются от черного (λi больше) до белого (λi меньше). Красные точки указывают, что пузырьки разрушились во время ККП.
Ученые обнаружили, что расположенные слева пузырьки равномерно разрушились. График 5b показывает распределение вероятностей в зависимости от среднего диаметра пузырька i (di) до и после ККП всех пузырьков. При этом диаметр (di) был рассчитан путем усреднения расстояния между центром и интерфейсом пузырька. Как мы видим, форма распределения вероятности на графике после ККП такая же, как и до ККП.
На графике 5с соотношение диаметра после ККП (da) и до ККП (db). Очевидно, что da = db, то есть диаметр пузырьков не изменялся во время каскадного коллапса.
График 5d показывает λi (характеристика анизотропии пузырька) до и после коллапса. Этот показатель также не изменился, несмотря на каскадный коллапс (λa (до ККП) = λb (после ККП); 5e).
Все эти наблюдения говорят о том, что форма пузырьков не меняется за счет каскадного разрушения пены, а также о том, что форма не влияет на этот процесс.
Следующий вероятный фактор, влияющий на процесс разрушения пены, это механическое воздействие разорванной пленки пузырька на своих соседей. Для определения влияния этого фактора ученые измерили скорость разрыва пленки при концентрации глицерина 17.8 % по формуле V = l / t, где l — длина пленки, а t — время, необходимое для поглощения пленки, от начала до конца.

Изображение №6
На графике 6а показано зависимость V от φ в виде логарифмического графика. Расчеты показывают, что V
10 м/с при концентрации глицерина в 17.8% (круги на графике). В случае концентрации глицерина 29% скорость практически не менялась (квадраты на графике).
При увеличении φ скорость снижается, за счет чего образующиеся во время разрыва пленки отскакивают от других каналов и, в итоге, поглощаются ими.
Также была изучена взаимосвязь между скоростью и осмотическим давлением (6b).
Формула давления для двумерной пены выглядит следующим образом:

где σ — поверхностное натяжение, R — средний радиус пузырька, φJ — точка заклинивания, равная 0,16 в двух измерениях.
В своем труде ученые применили такие показатели: σ = 37 мН/м и R = 1,7 мм.
Если предположить, что толщина слоя пленки составляет 1 мкм, то видна пропорциональная зависимость V от Π (6b). Следовательно, движущей силой поглощения является отрицательное давление в пленке.
Напоследок ученые провели анализ соотношения Ninner и скорости V (изображение ниже).

Изображение №7
Ученые выяснили, что показатель Ninner сильно увеличивается при росте скорости потока пленки. Таким образом, можно сделать вывод, что процесс проникновения является решающим элементом в процессе общего коллапса пены.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых.
Эпилог
В данном труде ученые смогли выяснить, что в момент разрушения пены основную роль играют два процесса — поглощение и распространение. Кроме этого ученые установили, что увеличение доли жидкости скорость капель, возникающих при разрушении пленки пузырька, снижается. Следовательно, сложнее разрушить всю пену. Вместо поглощения капли другой отдаленной пленкой происходит многократный отскок капли, и только потом поглощение.
Ученые намерены и дальше изучать пену, дабы понять ее слабые и сильные стороны. По их мнению, данный труд позволит усовершенствовать пену, сделав ее более долговечной и устойчивой. А такие преимущества могут пригодиться как в быту, так и в лабораториях, занимающихся производством и изучением различных биологических и химических веществ, материалов и прочего.
Кто бы мог подумать, что в XXI веке ученые будут изучать фактически пивную пену, выискивая способы сделать ее сильнее. Но, как бы странно это не звучало, любые знания важны, любые знания нужны. Понимание окружающего мира и всего, что его наполняет, позволяет нам лучше использовать то, что было изобретено или открыто уже давно, или усовершенствовать его в соответствии с постоянно меняющимися условиями нашей жизни.
Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята! 🙂
Молекулярная физика. Кипение жидкости.
Кипение — это интенсивный переход жидкости в пар, происходящий с образованием пузырьков пара по всему объему жидкости при определенной температуре.
В отличие от испарения, которое происходит при любой температуре жидкости, другой вид парообразования — кипение — возможен лишь при совершенно определенной (при данном давлении) температуре — температуре кипения.
При нагревании воды в открытом стеклянном сосуде можно увидеть, что по мере увеличения температуры стенки и дно сосуда покрываются мелкими пузырьками. Они образуются в результате расширения мельчайших пузырьков воздуха, которые существуют в углублениях и микротрещинах не полностью смачиваемых стенок сосуда.
Пары жидкости, которые находятся внутри пузырьков, являются насыщенными. С ростом температуры давление насыщенных паров возрастает, и пузырьки увеличиваются в размерах. С увеличением объема пузырьков растет и действующая на них выталкивающая (архимедова) сила. Под действием этой силы наиболее крупные пузырьки отрываются от стенок сосуда и поднимаются вверх. Если верхние слои воды еще не успели нагреться до 100 °С, то в такой (более холодной) воде часть водяного пара внутри пузырьков конденсируется и уходит в воду; пузырьки при этом сокращаются в размерах, и сила тяжести заставляет их снова опускаться вниз. Здесь они опять увеличиваются и вновь начинают всплывать вверх. Попеременное увеличение и уменьшение пузырьков внутри воды сопровождается возникновением в ней характерных звуковых волн: закипающая вода шумит.
Когда вся вода прогреется до 100 °С, поднявшиеся вверх пузырьки уже не сокращаются в размерах, а лопаются на поверхности воды, выбрасывая пар наружу. Возникает характерное бульканье — вода кипит.
Кипение начинается после того, как давление насыщенного пара внутри пузырьков сравнивается с давлением в окружающей жидкости.
Во время кипения температура жидкости и пара над ней не меняется. Она сохраняется неизменной до тех пор, пока вся жидкость не выкипит. Это происходит потому, что вся подводимая к жидкости энергия уходит на превращение ее в пар.
Температура, при которой кипит жидкость, называется температурой кипения.
Температура кипения зависит от давления, оказываемого на свободную поверхность жидкости. Это объясняется зависимостью давления насыщенного пара от температуры. Пузырек пара растет, пока давление насыщенного пара внутри него немного превосходит давление в жидкости, которое складывается из внешнего давления и гидростатического давления столба жидкости.
Чем больше внешнее давление, тем больше температура кипения.
Всем известно, что вода кипит при температуре 100 ºC. Но не следует забывать, что это справедливо лишь при нормальном атмосферном давлении (примерно 101 кПа). При увеличении давления температура кипения воды возрастает. Так, например, в кастрюлях-скороварках пищу варят под давлением около 200 кПа. Температура кипения воды при этом достигает 120°С. В воде такой температуры процесс варки происходит значительно быстрее, чем в обычном кипятке. Этим и объясняется название «скороварка».
И наоборот, уменьшая внешнее давление, мы тем самым понижаем температуру кипения. Например, в горных районах (на высоте 3 км, где давление составляет 70 кПа) вода кипит при температуре 90 °С. Поэтому жителям этих районов, использующим такой кипяток, требуется значительно больше времени для приготовления пищи, чем жителям равнин. А сварить в этом кипятке, например, куриное яйцо вообще невозможно, так как при температуре ниже 100 °С белок не сворачивается.
У каждой жидкости своя температура кипения, которая зависит от давления насыщенного пара. Чем выше давление насыщенного пара, тем ниже температура кипения соответствующей жидкости, т. к. при меньших температурах давление насыщенного пара становится равным атмосферному. Например, при температуре кипения 100 °С давление насыщенных паров воды равно 101 325 Па (760 мм рт. ст.), а паров ртути — всего лишь 117 Па (0,88 мм рт. ст.). Кипит ртуть при 357°С при нормальном давлении.
Теплота парообразования.
Теплота парообразования (теплота испарения) — количество теплоты, которое необходимо сообщить веществу (при постоянном давлении и постоянной температуре) для полного превращения жидкого вещества в пар.
Физическая величина, показывающая, какое количество теплоты необходимо, чтобы обратить жидкость массой 1 кг в пар без изменения температуры, называется удельной теплотой парообразования.
Удельную теплоту парообразования обозначают буквой r и измеряют в джоулях на килограмм (Дж/кг).
Количество теплоты, необходимое для парообразования (или выделяющееся при конденсации). Чтобы вычислить количество теплоты Q, необходимое для превращения в пар жидкости любой массы, взятой при температуре кипения, нужно удельную теплоту парообразования r умножить на массу m:
При конденсации пара происходит выделение такого же количества теплоты:
Скорость света ближе, чем казалось: ученые создали первый пузырь Алькубьерре
Еще одна технология из Star Trek оказалась больше наукой, чем фантастикой. Ученые под финансированием DARPA создали так называемую «warp bubble» — область пространства, способную расширяться или уменьшаться быстрее скорости света. Об этом сообщает бывший специалист НАСА по варп-двигателям Гарольд Уайт. Это первый настоящий «пузырь варп-движения», созданный в лаборатории. Который, как минимум, подтверждает, что такое возможно. И, по словам Уайта, устанавливает новую перспективу для тех, кто захочет создать первый космический корабль, способный к деформации.
Чтобы быть ясным, наше открытие — не аналог варп-пузыря, это настоящий, хотя и скромный и крошечный, варп-пузырь. Поэтому это так важно.
Теоретические двигатели быстрее скорости света

Доктор Гарольд «Сонни» Уайт
В 1994 году мексиканский математик Мигель Алькубьерре предложил первое математически правильное уравнение для варп-двигателя. Вдохновленный перелетами в Star Trek, он в общих чертах обрисовал двигательную установку космического корабля, которая может перемещаться по космосу быстрее скорости света без нарушения законов физики.
Это решение хвалили за элегантную математику, но одновременно высмеивали за использование «науки из сериала» и траты многих лет работы впустую над решением, которое казалось невозможным на практике.
Десять лет спустя теория Алькубьерре претерпела серьезные изменения, когда доктор Уайт, работавший тогда в НАСА, переработал исходную метрику Алькубьерре и привел ее в каноническую форму. Это изменение в дизайне двигателя резко сократило требования к экзотическим материалам и снизило необходимые затраты энергии. Тогда исследователи и поклонники научной фантастики получили проблеск надежды на то, что реальный варп-двигатель может однажды стать реальностью. Работа Уайта также привела к неофициальному переименованию первоначального теоретического проекта: теперь концепцию чаще называют «Варп-двигатель Алькубьерре/Уайта».
С тех пор многие физики и инженеры предпринимали попытки разработать жизнеспособный варп-двигатель, включая целую группу международных исследователей, работающих над двигателем варпа, не требующего никакой странной материи. Однако, как и Алькубьерре и Уайт до них, их концепции до сих пор оставались полностью теоретическими. Но теперь, похоже, ситуация изменилась.
Время — всё. Особенно на скорости света
Часто говорят, что время решает все. Поэтому неудивительно, что когда доктор Уайт начал свое последнее исследование, финансируемое DARPA, он и не думал о создании варп-пузыря. Ученые занимались исследованием геометрии пустот Казимира (наноскопической структуры, возникающей в результате эффекта, заставляющего две металлические пластины притягиваться в вакууме).
Не вдаваясь глубоко в сложную физику, лежащую в основе пустот Казимира и странных квантовых сил, наблюдаемых в этих структурах, достаточно сказать, что они никоим образом не связаны с механикой варп-двигателя. По крайней мере, так думали раньше. Но, по словам Уайта, они с его командой в LSI очень увлечены этой работой, а по мнению DARPA она имеет ряд возможных применений, выходящих далеко за рамки даже текущей находки.

Первый варп-пузырь
В итоге один из немногих ученых с интересом к варп-пузырям и пониманием уравнений Алькубьерре оказался в нужное время и в нужном месте. И заметил поразительное сходство между его текущим проектом и теоретическим микроскопическим двигателем, способным перемещаться быстрее скорости света.
Проверка учеными и подтверждение пузыря Алькубьерре
Фактические результаты, опубликованные после проверки в European Physical Journal, говорят:
При проведении анализа, связанного с проектом, финансируемым DARPA, по оценке возможной структуры плотности энергии, присутствующей в полости Казимира, как это предсказано динамической моделью вакуума, была обнаружена наноразмерная структура, которая предсказывает распределение плотности отрицательной энергии, которое близко соответствует требованиям метрики Алькубьерре.
Или, проще говоря, как говорит Уайт, «Насколько мне известно, это первая статья в рецензируемой литературе, которая говорит о реальной наноструктуре, которая, по прогнозам, будет являться настоящим, хотя и скромным, пузырем деформации».
Это случайное открытие, по словам Уайта, не только подтверждает предсказанную «тороидальную» структуру варп-пузыря и наличие в нем отрицательной энергии, но также дает потенциальный путь другим исследователям, пытающимся спроектировать, а в один прекрасный день и построить настоящий космический корабль, способный на перемещение путем искажения пространства-времени вокруг себя.
«Эта потенциальная структура будет генерировать отрицательное распределение плотности энергии вакуума, которое очень похоже на то, что требуется для деформации пространства Алькубьерре».
Путь вперед
Чтобы оценить возможные перспективы, Уайт и его команда разработали проект тестируемого наномасштабного «корабля с варп-двигателем». Во время его презентации AIAA (крупнейшему в мире аэрокосмическому техническому сообществу) он объяснил:
Мы проанализировали игрушечную модель двигателя, состоящую из сферы диаметром 1 микрон, расположенной в центре цилиндра диаметром 4 микрона. Она показала трехмерную плотность энергии Казимира, которая хорошо коррелирует с требованиями метрик Алькубьерре.
Эта качественная корреляция предполагает, что мы можем проводить эксперименты в масштабе наночипа, чтобы попытаться измерить крошечные сигнатуры. Но пока что мы видим наглядную иллюстрацию реального, хотя и очень скромного по размерам, варп-пузыря деформации.
Уайт развил эту идею в электронном письме в The Debrief:
Мы уже можем предложить сообществу структуру, которая генерирует отрицательное распределение плотности энергии вакуума, очень похожее на то, что требуется для деформации космоса Алькубьерре.
Уайт говорит, что такие мини-двигатели уже можно производить — если использовать 3D-принтер GT, печатающий в нанометровом масштабе. Но в настоящее время ученые продолжают заниматься тем, на что получили финансирование — исследовании свойств полостей Казимира. А постройкой кораблей и масштабированием двигателей для них могут заняться все остальные.

Предложение для следующего эксперимента
Уайт и его команда даже предлагают путь для дальнейших исследований. По их словам, стоит построить эксперимент, включающий несколько созданных пустотами Казимира варп-пузырей, стоящих друг за другом в виде цепочки. По их словам, такая конструкция позволит лучше понять физику структуры варп-пузыря, а также то, сможет ли корабль однажды пересечь реальное пространство внутри такого пузыря.
Уайт на конференции AIAA объяснил:
Мы могли бы провести исследование оптических свойств этих маленьких, наноразмерных пузырей деформации. Если объединить большое количество из них подряд, мы можем намного усилить эффект, чтобы можно было его увидеть и изучить.
Ползти, идти, бежать
Учитывая, что DARPA платит лаборатории LSI Eagleworks за исследование полостей Казимира, а не за случайное открытие пузыря искривления пространства-времени, независимо от его (потенциально) невероятных последствий Уайт и его команда не могут бросить свой текущий проект. Поэтому призывают других ученых попробовать реализовать варп-пузыри и протестировать их свойства. Поскольку DARPA принадлежит Министерству обороны США, публично обнародовать результаты проектов им сложно. Текущий прорыв был достигнут еще в начале лета, а говорить о нем в деталях стало можно только сейчас. И это при том, что исследование полостей Казимира официально не было засекреченным, что и позволило ученым в итоге выйти на публику.
Если DARPA профинансирует работу LSI над космическим кораблем с наноразмерным варп-двигателем, о таком проекте мы можем не услышать еще много лет.
В конце концов, особенно с учетом масштабов этого открытия и его потенциальных последствий, Уайт считает, что создание и испытание его мини-варп-корабля — это лишь вопрос времени. По его мнению, теперь наука будет медленно, но верно продвигаться к этой цели в виде космического корабля, способного к деформации.
Когда его спросили, как быстро протестированный наноразмерный «корабль» может быть масштабирован до чего-то, на чем действительно можно было бы летать в космос, Уайт предложил более реалистичный подход к этому исследованию:
Еще рано задавать вопросы о каких-то реальных летательных экспериментах. На мой взгляд, первый шаг — просто изучить основную науку в нано / микромасштабе. И постепенно пытаться переходить к чему-то более крупному. Сначала мы должны научиться ползать, потом — идти, и только потом — бежать.
Дополнительный разбор того, что становится возможным с варп-двигателем, на Хабре есть тут.
Перевод статьи научного журнала TheDebrief.
Первая презентация варп-пузыря Уайтом на Propulsion Energy Forum доступна на ютубе. Тогда его находка еще не была проверена научным сообществом.
Хотите найти крутую работу? Подключайте телеграм-бот g-mate. Указываете желаемую зарплату, и он выдает вам лучшие вакансии от топовых компаний, и помогает пройти интервью. Для старта не нужно ни резюме, ни портфолио, настройка занимает меньше 30 секунд.