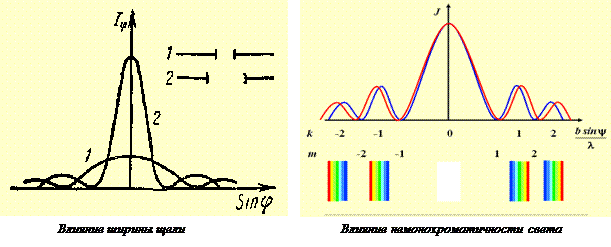Что такое пятно пуассона
Пятно Пуассона
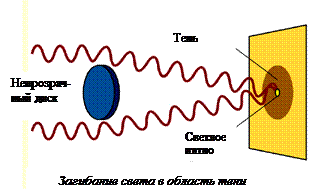
С помощью спирали Френеля можно получить еще один замечательный результат. Действительно, если на пути сферической волны находится непрозрачное круглое отверстие (любого размера), то оказывается закрытым какое-то число внутренних зон Френеля. Но вклад в колебания в точке наблюдения, находящегося в центре геометрической тени,будут давать остальные зоны. В результате в этой точке должен наблюдаться свет.
Этот результат показался в свое время Пуассону столь невероятным, что он выдвинул его как возражение против рассуждений и расчетов Френеля при рассмотрении дифракции. Однако, когда был проведен соответствующий опыт, такое светлое пятнышко в центра геометрической тени было обнаружено. С тех пор оно носит название пятна Пуассона, хотя он не допускал и самой возможности его существования.
Пятно Пуассона – светлое пятно в центре геометрической тени от непрозрачного объекта. Пятно Пуассона обусловлено загибанием света в область геометрической тени.
Пятно Араго — Пуассона
Пятно Араго — Пуассона (иногда просто пятно Пуассона) — это яркое пятнышко, возникающее за освещённым направленным пучком света непрозрачным телом в его области геометрической тени.
Это явление стало одним из веских подтверждений волновой теории света. Существование этого пятна показал теоретически в 1818 г. Симеон Дени Пуассон на основе предложенной Огюстеном Френелем теории. Получалось, что за большим круглым непрозрачным телом прямо в середине его геометрической тени должно возникать небольшое светлое пятно. Очевидную абсурдность этого результата Пуассон хотел использовать как главный аргумент против теории дифракции Френеля, однако Доминик Араго поставил эксперимент, подтвердивший это предсказание. В итоге этот результат, ставший известным как пятно Араго — Пуассона, оказался весомым аргументом в пользу новой волновой теории.
Содержание
Объяснения эффекта
Элементарное
Существование пятна Араго — Пуассона легко объяснить на основании принципа Гюйгенса — Френеля. Предположим, что на круглый непрозрачный диск падает плоская волна, параллельная оси диска. Согласно принципу Гюйгенса — Френеля, точки на краю диска можно рассматривать как источники вторичных волн, причём все они будут когерентны. Все эти волны пройдут одинаковое расстояние от края диска до любой точки на его оси. В результате они придут в эту точку в одинаковой фазе и усилятся, создавая яркое пятнышко. Стоит отметить, что на достаточно больших расстояниях от диска наблюдать пятно становится невозможно, в силу пространственной декогерентности приходящих волн.
Теория рассеяния
Существование пятна Араго — Пуассона может быть частично объяснено на основе общей теории рассеяния. Полное сечение рассеяния σtot света на препятствии и (комплексная) амплитуда рассеяния f связаны соотношением
называемым оптической теоремой. Здесь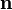 
— направление падающего пучка. Отсюда, в силу непрерывности амплитуды рассеяния как функции направления рассеяния, следует, что дифференциальное сечение рассеяния вперёд
отлично от нуля, что соответствует светлому пятну позади тела. Отметим, что это объяснение не вполне точное, так как описание света с помощью амплитуды и сечения рассеяния возможно лишь на расстоянии, большом по сравнению с размерами тела, но на таких расстояниях становится существенным учёт когерентности волн, а кроме того становится невозможным точно сопоставить размеры геометрической тени тела и соответствующего светлого пятна.
Пятно Пуассона
Это явление стало одним из веских подтверждений волновой теории света. Существование этого пятна показал теоретически в 1818 году Симеон Дени Пуассон на основе предложенной Огюстеном Френелем теории. Получалось, что за большим круглым непрозрачным телом прямо в середине его геометрической тени должно возникать небольшое светлое пятно. Очевидную абсурдность этого результата Пуассон хотел использовать как главный аргумент против теории дифракции Френеля, однако Доминик Араго поставил эксперимент, подтвердивший это предсказание. В итоге этот результат, ставший известным как пятно Араго — Пуассона, оказался весомым аргументом в пользу новой волновой теории. При дифракции на открытом отверстии можно наблюдать противоположный эффект – тёмное пятно.
Связанные понятия
При рассмотрении сложного движения (когда точка или тело движется в одной системе отсчёта, а эта система отсчёта в свою очередь движется относительно другой системы) возникает вопрос о связи скоростей в двух системах отсчёта.
Согласно концепции переме́нной ско́рости све́та (ПСС) считается, что скорость света в вакууме, обычно обозначаемая c, в некоторых случаях может не быть константой. В большинстве ситуаций в физике конденсированного состояния распространение света в среде действительно происходит с меньшей скоростью, чем в вакууме. Кроме того, в некоторых расчётах квантовой теории поля необходимо учитывать, что виртуальные фотоны должны двигаться на короткие расстояния в том числе со скоростью, отличной от скорости.
Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой. Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость.
Интерфере́нция в тóнких плёнках – явление, которое возникает в результате разделения луча света при отражении от верхней и нижней границ тонкой плёнки. В результате возникают две световые волны, которые могут интерферировать. Тонкоплёночная интерференция объясняет цветовую палитру, видимую в свете, отраженном от мыльных пузырей и масляных плёнок на воде. Это явление также является основополагающим механизмом, используемым в объективах камер, зеркалах, оптических фильтрах и антибликовых покрытиях.
В астрономии и космологии темная жидкость является альтернативой теории как темной материи, так и темной энергии и пытается объяснить оба явления в единой структуре.Темная жидкость предполагает, что темная материя и темная энергия не являются отдельными физическими явлениями, как считалось ранее, и не имеют отдельного происхождения, но они тесно связаны друг с другом и могут рассматриваться как две грани одной жидкости. В галактических масштабах темная жидкость ведет себя как темная материя, а в.
Пятно Араго-Пуассона
Существование пятна Араго-Пуассона легко объяснить на основании принципа Гюйгенса-Френеля(sic!). Предположим, что на круглый непрозрачный диск падает плоская волна, параллельная оси диска. Согласно принципу Гюйгенса-Френеля, точки на краю диска можно рассматривать как источники вторичных волн, причём все они будут когерентны. Все эти волны пройдут одинаковое расстояние от края диска до любой точки на его оси. В результате они придут в эту точку в одинаковой фазе и усилятся, создавая яркое пятнышко. Стоит отметить, что на достаточно больших расстояниях от диска наблюдать пятно становится невозможно, в силу пространственной декогерентности приходящих волн.
Тень от монеты в €2 на расстоянии в 62 м.
Тут ещё неплохо бы рассказать про историю возникновения тандема Араго-Пуассон у названия данного эффекта. Дело в том, что после доклада Араго в Парижской академии наук по поводу теории волновой оптики его друг и видный ученый Пуассон заметил (не на пустом месте, а так как уже изучал эту теорию и теоретически определил такую возможность), что если эта странная волновая теория вообще хоть как-то верна, то у тени загораживающего от когерентного источника экрана в центре должна появиться световая точка. Сказал он это с сарказмом (не едким, конечно), так как тогда ещё во всю правила корпускулярная точка зрения Ньютона на природу света и Симеон Дени Пуассон был её последователем. А вот про то, как он лично отреагировал на эксперимент Араго с непосредственным наблюдением этого пятна я, к сожалению, нигде не нашёл.
Не тяжеловата лекция, для второго то января?
Объясните откуда взялось 62м? На видео там сантиметров 15
Причем тут (sic!)?
https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%93%D1%8E%D0%B9%D0%B3%D0%B5%D0%BD%D1%81%D0%B0_%E2%80%94_%D0%A4%D1%80%D0%B5%D0%BD%D0%B5%D0%BB%D1%8F
что вы гоните. это плазмоиды.
думал, что мне напоминает фотография.
Точно, так же линзы выглядят в театральных прожекторах с лампами накаливания!
Они называются линзами Френеля.
(мы их френельками зовём))
Не понял, почему вторичные волны будут когерентными.
Пчёлы
Мыльный пузырик
Тайна снежинок (Veritasium)
Какие тайны скрывает процесс образования снежинок, обеспечивающий такое широкое разнообразие форм и сложность узора? Как выращивать снежинки в лабораторных условиях, влияя всего на два параметра: температуру и влажность, чтобы приблизиться к пониманию того, как работает формообразование кристаллов льда?
Там, на неведанных дорожках, следы невиданных зверей.
Виды береговой защиты
Все вы наверняка видели различные виды береговой защиты на набережных и пляжах. И вот, как они снижают риски подтопления.
Музыка грибов
Ничего такого, просто биоэлектричество гриба преобразуется в ноты синтезатора
Отец и сын
В 1906 году Джозеф Джон Томсон получил Нобелевскую премию по физике за демонстрацию того, что электрон является элементарной частицей, а в 1937 году его сын Джордж Паджет Томсон получил Нобелевскую премию за то, что показал, что электрон может быть волной.
Больше околонаучного на канале https://t.me/everScience.
Шикарный клюв со всех сторон
Китоглав, или королевская цапля (лат. Balaeniceps rex) — птица из отряда пеликанообразных, единственный представитель семейства китоглавых (Balaenicipitidae).
Очень крупная птица, её высота в среднем составляет 1,2 м, размах крыльев — 2,3 м, а вес — от 4 до 7 кг.
Обитает в тропических болотах Восточной Африки, где водятся двоякодышащие рыбы протоптеры — его главный корм.
Похожий на деревянный башмак клюв делает китоглава искусным мастером рыбной ловли.
В отличие от большинства других птиц, глаза китоглава расположены в передней части черепа, а не с двух сторон, что позволяет ему иметь бинокулярное зрение. Ввиду массивности клюва птица кладёт его на грудь во время отдыха.
Китоглав был открыт в 1849 году, менее чем через год он был уже научно описан.
Tokyo Safari, Yokohama, Japan
Сафари-парк в Японии
Квантовая теория поля: визуализация от ScienceClic
Как согласовать теорию относительности с квантовой механикой? Что такое спин? Откуда берётся электрический заряд?
Вдогонку к посту «Прыгаем в чёрную дыру»
Бонусное видео с прыжком в чёрную дыру. Без комментариев и под атмосферное музыкальное сопровождение. Сделано в формате 360 градусов, так что можно покрутить и наблюдать от первого лица эффекты, описанные в основном видео с теорией.
Прыгаем в чёрную дыру (ScienceCLic)
Как выглядит чёрная дыра? Какие оптические эффекты возникают в непосредственной близости от неё? Что мы увидим при пересечении горизонта событий?
Для визуализации использовались расчёты и симуляции.
Почему занавеска в душе хочет к вам прилипнуть
31-летний профессор машиностроения Дэвид Шмидт из Университета Массачусетса в Амхерсте в 2001 году получил Шнобелевскую премию за то, что на софте за 28 000 долларов для моделирования потоков жидкостей просчитал модель, частично объясняющую, почему занавеска хочет прилипнуть к вам в душе. (Публикация в Scientific American )
Дэвид Шмидт исследовал способы точной имитации брызг и распыления (spray). Обычно они использовали эти симуляции распыления, чтобы помочь разработать лучшие дизельные и авиационные двигатели. Однако тот же анализ в равной степени применим и к душевой кабине в ванной. В конце концов, душ — это просто большая струя брызг.
В своей симуляции Дэвид Шмидт учел эффекты дробления капель, модель также учитывала деформацию (distortion) капель, которая существенно влияет на аэродинамическое сопротивление.
Все предыдущие объяснения были теоретические: от эффекта Бернулли (Bernoulli effect) до теории плавучести (buoyancy effect).
Гипотеза эффекта Бернулли
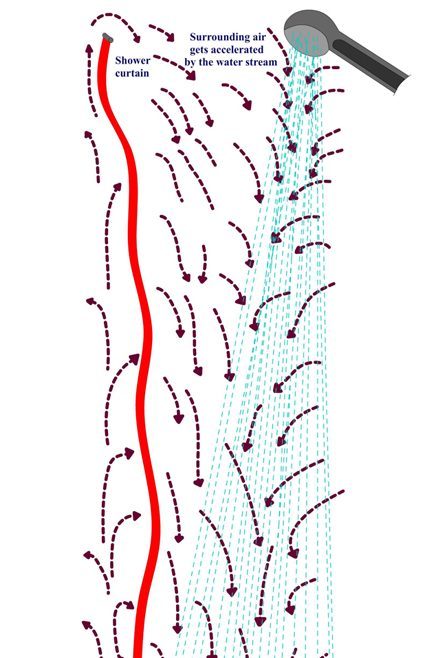
Самым популярным объяснением эффекта занавески для душа является принцип Бернулли. Принцип Бернулли гласит, что увеличение скорости приводит к снижению давления. Эта теория предполагает, что вода, вытекающая из насадки для душа, заставляет воздух, через который движется вода, течь в том же направлении, что и вода. Это движение будет параллельно плоскости занавески для душа. Согласно принципу Бернулли, если воздух движется по внутренней поверхности занавески для душа, давление воздуха там упадет. Это приведет к перепаду давления между внутренним и внешним пространством, что приведет к перемещению занавески внутрь. Эффект будет наиболее сильным, когда зазор между человеком и занавеской будет наименьшим, в результате чего занавеска будет прилипать к человеку.
Но эффект Бернулли основан на соотношении давления и ускорения и не учитывает наличия капель. И, по расчетам лауреата Шнобелевской премии, этот эффект не отвечает за прогиб занавески в душе.
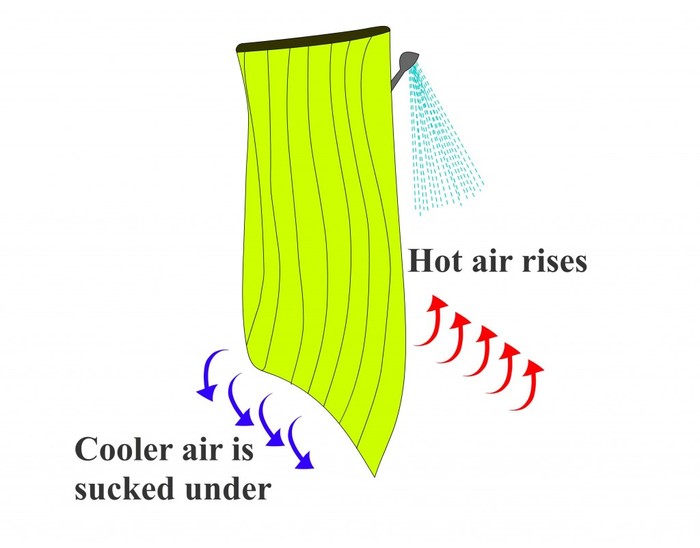
Также называемый эффектом дымохода или эффектом стека/тяги, подразумевает, что теплый воздух (из горячего душа) поднимается над занавеской душа, когда более прохладный воздух (около пола) проталкивается под занавеску, заменяя поднимающийся воздух. Если придвинуть занавеску к струе, вихрь (ближнего действия) и эффекты Коанда становятся более значительными. Однако эффект занавески для душа сохраняется при использовании холодной воды, что означает, что это не может быть единственным действующим механизмом.
Теория плавучести предполагает, что горячий душ вызывает повышение температуры воздуха в душе, уменьшая его плотность. В этом случае давление на душевой стороне занавески будет ниже, чем давление снаружи на той же высоте от пола, что приведет к смещению занавески в сторону более низкого давления. Проблема с этим объяснением состоит в том, что занавеска так же будет втягиваться внутрь к холодному душу.
Эффект Коанда, также известный как «прикрепление пограничного слоя», представляет собой тенденцию движущейся жидкости прилипать к соседней стене.
Пятно Пуассона или дифракция на непрозрачном диске
Пусть на пути плоской волны расположен непрозрачный круглый диск. Согласно представлениям геометрической оптики область на экране – это область геометрической тени. Т.к. первые m зон отсутствуют, результирующая амплитуда в точке Р равна
Е = Еm+1 – Е m+ 2 + Е m+ 3 – Е m+ 4 + ……± Е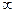 
= Еm+1/2,
Мы видим, что если число перекрытых диском зон не слишком велико, так что убыванием Е можно пренебречь, амплитуда колебаний в центре тени от диска, практически такая же, какая была бы в точке Р при отсутствии диска. Таким образом, независимо от числа перекрываемых диском зон, векторная амплитуда в осевой точке оказывается конечной, монотонно возрастая по мере уменьшения диаметра диска.
 |
3.1.3. СПИРАЛЬ ФРЕНЕЛЯ – МЕТОД ГРАФИЧЕСКОГО СЛОЖЕНИЯ АМПЛИТУД.Рассмотрим графический метод сложения амплитуд. В этом методе мысленно разбивают волновую поверхность на узкие кольцевые подзоны, число которых велико. Амплитуда вторичных волн, изображается вектором, длина которого пропорциональна амплитуде, а фаза – углом наклона к оси абсцисс. В пределе при стремлении ширины кольцевых зон к нулю (количество их будет при этом неограниченно возрастать) векторная диаграмма принимает вид спирали, закручивающейся к ее центру (рис.).
 |
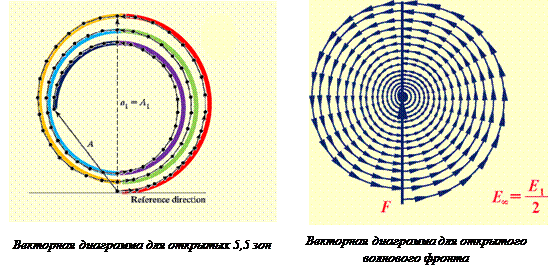Проследим за изменением получающихся диаграмм при постепенном увеличении диаметра отверстия в непрозрачном экране.Каждая зона на диаграмме представляет половину окружности. При переходе к следующее зоне
На рисунках показаны векторные диаграммы для случая, когда размер отверстия в непрозрачном экране постепенно пропускает
· 
первую зону Френеля (вектор Е1),
Цепочка по мере увеличения числа m закручивается в спираль и в результате действие всех зон Френеля (открытый волновой фронт) амплитуда поля в точке наблюдения вдвое меньше, чем при одной открытой первой зоне: амплитуда колебаний определяется длиной вектора Ео, проведенным из начала спирали в ее фокус.
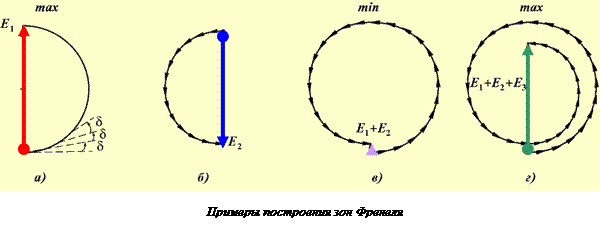
Т. о., амплитуда колебаний в точке Р по мере увеличения радиуса отверстия меняется не монотонно: максимум сменяется минимумом и т.д. То же самое произойдет, если приближать точку наблюдения, т.е уменьшать расстояние b (рис.). Причем амплитуда (интенсивность) света максимальна в точке наблюдения на расстоянии, при котором отверстие совпадает с первой зоной Френеля.
3.1.4. ЗОННЫЕ ПЛАСТИНКИ. ИЗМЕНЕНИЕ ФАЗОВЫХ СООТНОШЕНИЙ МЕЖДУ ВТОРИЧНЫМИ ВОЛНАМИ.Из теории дифракции Френеля вытекает возможность управления формой волнового фронта и распределением интенсивности посредством изменения фазовых соотношений между вторичными волнами. Две соседние зоны действуют как источники света, колеблющиеся в противофазе — посылаемые ими световые волны в значительной степени гасят друг друга за счет деструктивной интерференции. Все четные зоны Френеля дают вклад в результирующее поле одного знака. Все нечетные – противоположного знака. Если все четные (или нечетные) зоны закрыть непрозрачной маской, то, амплитуды этих зон сонаправлены и в точке Р будет наблюдаться многократное усиление света (рис. а). По закону сохранения энергии в других точках пространства интенсивность света должна уменьшиться, то есть произойдет фокусировка света в точку Р. Такая маска называется амплитудной зонной пластинкой.На спирали Френеляостаются «работающими» только полувитки, отвечающие нечетным зонам; полувитки четных зон «выбывают из игры», поскольку заполняющие их вторичные источники оказались затененными. Амплитуда результирующего колебания Е равна при этом сумме амплитуд слагаемых колебаний, а
 |
интенсивность для к открытых зон. Зонная пластинка Френеля обладает фокусирующими свойствами, существенно увеличивая интенсивность света в точке Р, которая является точкой фокусировки зонной пластинки.
 |
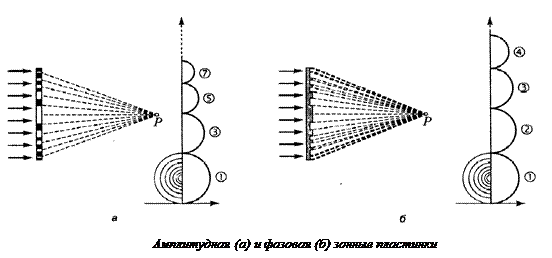Если вместо непрозрачной маски для четных (нечетных) зон ввести дополнительный фазовый сдвиг Dj = л, т. е. использовать свет всех зон, интенсивность света в фокусе возрастет еще в 4 раза. Искомого фазового сдвига можно добиться, например, путем размещения в отверстии стеклянной пластины с кольцевыми ступенями равной высоты h. Вносимая ступенькой разность хода составит
 |
где n – показатель преломления пластины. В этом случае пластинка называется фазовой.
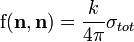
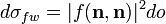
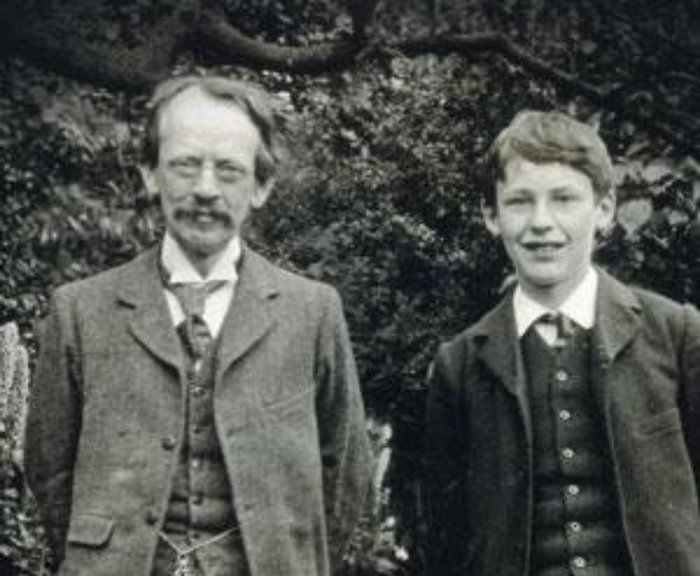
Ключевые понятия:
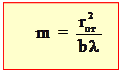
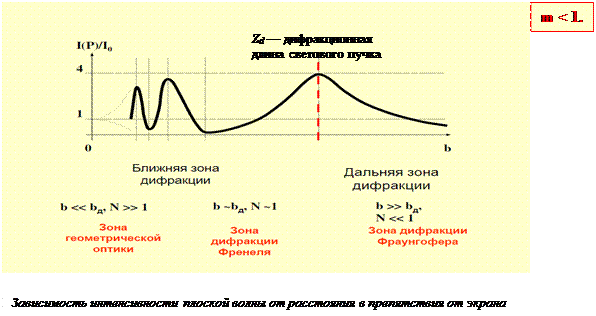
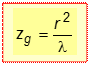
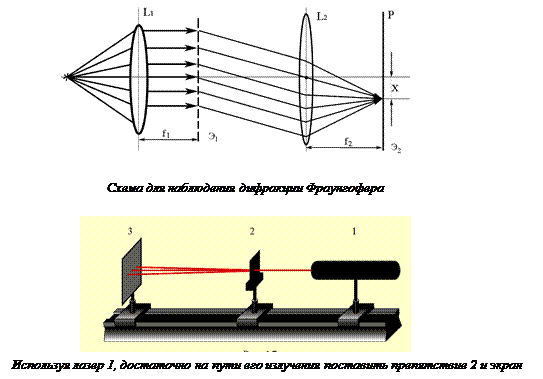
3.2.4. ВЛИЯНИЕ ШИРИНЫ ЩЕЛИ НА РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ. Запишем выражение для угловой ширины главного максимума. Она равна угловому расстоянию между двумя первыми минимумами: