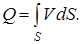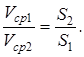Что такое расход в гидравлике
Измерение расхода жидкости: приборы и методы
Расход – это объем жидкости протекающий в единицу времени через поперечное сечение трубопровода. Измерение расхода жидкости является одной из задач при производственных испытаниях оборудования.
В этой статье мы собрали для Вас все современные методы определения расхода жидкости, а так же приборы для измерения расхода: трубчатые расходомеры, расходомерные шайбы, крыльчатые расходомеры, ультразвуковые и вихревые расходомеры.
Содержание статьи
Методы измерения расхода жидкости
Наиболее простые и вместе с тем точные методы измерения расхода жидкости являются объемный и массовый (весовой).
В соответствии с методами измерения, единицами расхода жидкости являются:


При объемном способе измерения протекающая в исследуемом потоке(например, в трубе) жидкость поступает в особый, тщательно протарированный сосуд (так называемый мерник), время наполнения которого точно фиксируется по секундомеру.
Если известен объем мерника – V и измеренное время его наполнения – T, то объемный расход будет
При весовом способе взвешиванием находят вес Gv = mv*g (где g – ускорение свободного падения) всей жидкости, поступившей в мерник за время T. Затем определяют её массу
и по ней, зная плотность жидкости (ρ), вычисляют объемный расход
Но объемный и весовой методы измерения расхода жидкости пригодны только при сравнительно небольших значениях расхода жидкости, так как в противном случае размеры мерников получаются довольно громоздкими и, как следствие, замеры очень затруднительными.
Кроме того, этими способами невозможно измерить расход в произвольном сечении, например, длинного трубопровода или канала без нарушения их целостности. Поэтому, за исключением случаев измерения сравнительно небольших расходов жидкостей в коротких трубах и каналах, объемный и весовой способы, как правило, не применяются, а на практике пользуются специальными приборами, которые предварительно тарируются объемным или весовым способом.
Приборы для измерения расхода жидкости
Трубчатые расходомеры
Одним из таких приборов является трубчатый расходомер или расходомер Вентури. Большим достоинством этого расходомера является простота конструкции и отсутствие в нем каких-либо движущихся частей. Трубчатые расходомеры могут быть горизонтальными и вертикальными. Рассмотрим, к примеру, горизонтальный вариант.
Расходомер состоит из двух цилиндрических труб А и В диаметра d1, соединенных при помощи двух конических участков (патрубков) С и D с цилиндрической вставкой E меньшего диаметра d2. В сечениях 1-1 и 2-2 расходомера присоединены пьезометрические трубки a и b, разность уровней жидкости h в которых показывает разность давлений в этих сечениях.
Расход жидкости в этом случае определяется по тарировочным кривым, полученным опытным путем и дающим для данного расходомера прямую зависимость между показаниями манометра и измеряемыми расходами жидкости. Пример такой кривой на картинке рядом
Расходомерная шайба
Другим широко распространенным прибором для измерения расхода является расходомерная шайба (или диафрагма), обычно выполняемая в виде плоского кольца с круглым отверстием в центре, устанавливаемого между фланцами трубопровода
Края отверстия чаще всего имеют острые входные кромки под углом 45° или закругляются по форме втекающей в отверстие струи жидкости (сопло). Два пьезометра a и b (или дифференциальный манометр) служат для измерения перепада давления до и после диафрагмы. В основе метода положен принцип неразрывности Бернулли.
Расход в этом случае определяется по замеренной разности уровней в трубках. Трубки подсоединяют к датчикам, замеряющим перепад давления. Датчик перепада давления преобразует перепад в электрический сигнал, который отправляется на компьютер.
Крыльчатый расходомер
Расходы могут быть вычислены также в результате измерения скоростей течения жидкости и живых течений потока.
Одним из широко распространенных приборов, применяемых для этой цели является гидрометрическая вертушка. Современный турбинный расходомер устанавливают только на горизонтальном участке трубопровода. Лопасти крыльчатки колеса турбины изготавливают из не магнитного материала.
Вертушка состоит из крыльчатки А, представляющей собой колесо с винтовыми лопастями, насаженное на горизонтальный вал С. Когда она установлена в потоке, крыльчатка под действием протекающей жидкости вращается, причем число её оборотов прямо пропорционально скорости течения. Число импульсов за один оборот крыльчатки равно числу лопастей, а значит частота импульсов пропорциональна расходу.
При вращении лопасти поочередно пересекают магнитное поле, которое наводит электродвижущую силу в катушке в виде импульса. От вертушки вверх выводятся провода В, подающему сигнал к специальному счетчику, автоматически записывающему число оборотов и время.
Приборы для измерения расхода жидкости в этом случае называют турбинными расходомерами
Ультразвуковой метод измерения расхода
Ультразвуковой расходомер работает по принципу использования разницы по времени прохождения ультразвукового сигнала в направлении потока и против него.
Расходомер формирует электрический импульс, поступающий на пьезоэлемент П1, который излучает электромеханические колебания в движущуюся среду. Эти колебания воспринимаются через некоторое время пьезоэлементом П2, преобразуются им в электрический импульс, попадающий в электронное устройство и снова направляемый им на пьезоэлемент П1 и т.д.
Такой контур П1-П2 характеризуется частотой f1 повторений импульсов, прямо пропорциональной расстоянию между пьезоэлементами и обратно пропорциональной разности между скоростью распространения звука в контролируемой среде и скоростью самой среды.
Аналогично электронное устройство подает импульсы в обратном направлении, т.е. от пьезоэлемента П2 к пьезоэлементу П1. Контур П2-П1 характеризуется своей частотой f2 повторений импульсов, прямо пропорциональной расстоянию между пьезоэлементами и обратно пропорциональной сумме скоростей распространения звука в среде и самой среды.
Следующим шагом является определение разности Δf указанных частот, которая пропорциональна расходу среды. Приборы для измерения расхода жидкости называются ультразвуковые расходомеры.
Вихревой метод измерения расхода
В основу работы вихревых расходомеров положена зависимость между расходом и частотой возникновения вихрей за твердым телом (например, металлическим прямоугольным стержнем), которое расположено в потоке жидкости или газа.
Принцип действия преобразователя основан на ультразвуковом детектировании вихрей, образующихся в потоке жидкости, при обтекании жидкостью специальной призмы, расположенной поперек потока.
В зависимости от конструкции датчика чувствительные тепловые элементы устанавливаются непосредственно в теле датчика или вихревой дорожке.
Если в тело образующее вихри, установить магнит, то он может служить датчиком. Реакция, возникающая при срыве вихрей, заставляет помещённый в поток цилиндр колебаться с частотой вихреобразования. Достоинством вихревых расходомеров является, обеспечение низкой зависимости качества измерений от физико-химических свойств жидкости, состояния трубопровода, распределения скоростей по сечению потока и от точности монтажа первичных преобразователей на трубопроводе. Приборы для измерения расхода жидкости называются вихревые расходомеры.
Видео о измерении расхода
При проведении измерения расхода, в некоторых случая используется понятие количества вещества – это количество жидкости или другой среды, проходящей через поперечное сечение трубопровода в течении определенного промежутка времени(за час, месяц, рабочую смену и т.д.)
Приборы для измерения количества вещества по аналогии с измерением расхода монтируются на – на трубопроводе, с выводом вторичного прибора к оператору.
Расход жидкости
Вы здесь
Жидкими телами называются физические тела, легко изменяющие свою форму под действием сил незначительной величины.
Течение жидкости характеризуется ее расходом, величина которого определяется как произведение площади поперечного сечения поршня на скорость его движения.
Расход = площадь поперечного сечения ∙ скорость перемещения
Для общего понимания, что такое расход жидкости, давайте рассмотрим на примере.
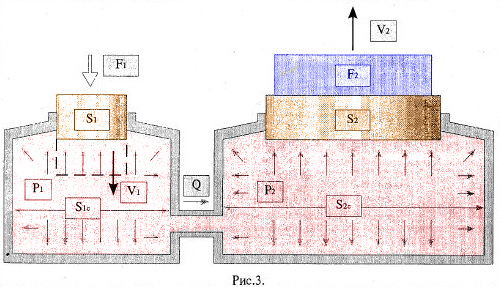
Если в поршень в первом сосуде, изображенном на рис.3, перемещать вниз с некоторой скоростью, которая обычно обозначается латинской буквой “V”, одновременно воздействуя на него усилием F1, то он будет вытеснять жидкость во второй сосуд. Поршень, которого будет подниматься со скоростью во столько раз меньшей скорости опускания поршня в первом сосуде, во сколь раз площадь его поперечного сечения больше площади поперечного первого поршня.
В Технической литературе расход жидкости обозначается латинской буквой “Q” и может быть представлен также как произведение объема жидкости перемещаемого за единицу времени:
расход = (перемещаемый объем)/время
Соответственно, выражение для расхода жидкости может быть представлено в виде:
Буквой “W” обозначена величина вытесняемого объема жидкости, а “t” – время вытеснения, или Q=S∙V. Так как V1c∙ S1с= V2∙S2с, поскольку объем жидкости, вытесненный за некоторое время из первого сосуда, поступил во второй сосуд за это же время, а значит расход жидкости вытекающей из первого сосуда, равен расходу жидкости, поступающий во второй сосуд:
Жидкость во втором сосуде будет течь медленнее во столько раз, во сколько раз площадь поперечного сечения этого сосуда больше площади сечения первого сосуда (буквами S1с и S2с обозначены площади сечения сосудов),а S1 и S2 (площади сечения их горловин).
Единицы измерения расхода
Наиболее часто на практике встречаются следующие единицы измерения расхода:
В европейских странах используются также величины dm 3 ⁄min (кубические дециметры отнесенные к минуте), которая численно равна л/мин.
В Англии, США и Японии используется величина, представляющая собой отношение объёма, выраженного в имперских галлонах, к минуте и обозначается, как “imgalpm” и “galpm”. Пересчет этих величин в л/мин может быть выполнен по соотношению: 1 imgalpm = 4.5 л/мин и 1 galpm = 3,8 л/мин.
Расходом называется количество жидкости, протекающее через живое сечение потока (струйки) в единицу времени. Количество жидкости можно задать объемом, массой или весом. Соответственно и расходы бывают объемный Q, массовый Qm и весовой QG.
Для элементарной струйки, имеющей бесконечно малые площади живых сечений, можно считать скорость жидкости в любой точке сечения одинаковой. Тогда
dQ = V dS; dQm=r dQ = rV dS; dQG= g dQm= grV dS,
где dS – площадь живого сечения струйки.
Для потока конечных размеров скорость в различных точках сечения будет различной, поэтому расход следует определять как сумму элементарных расходов струек
Но это чисто теоретическая формула, воспользоваться ей для определения расхода проблематично. Обычно вводят в рассмотрение среднюю по сечению скорость потока, которую можно найти по измерянному расходу
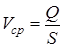
Основываясь на законе сохранения вещества, на предположении о неразрывности (сплошности) потока и на свойстве непроницаемости трубки тока, для стационарного течения несжимаемой жидкости можно утверждать, что объемный расход во всех сечениях элементарной струйки один и тот же:
dQ = V1 dS1 = V2 dS2 = const (вдоль струйки).
Это уравнение объемного расхода для элементарной струйки.
Аналогичное уравнение можно записать и для потока конечных размеров, ограниченного непроницаемыми стенками, только скорости следует брать средние
Q = Vср1 S1 = Vсp2 S2 = const (вдоль потока).
Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям живых сечений:
Уравнение расхода – это частный случай закона сохранения вещества для условий неразрывности потока.
Поможем написать любую работу на аналогичную тему
Понятие расхода. Характеристики потока среды
ПОНЯТИЕ РАСХОДА:
Объемный расход определяется по формуле:
Q = V • S,
где Q — объемный расход;
V — скорость потока;
S — площадь поперечного сечения потока.
Массовый расход определяется через плотность и объемный расход:
Qm = Q • ρ,
где Qm — массовый расход;
ρ — плотность измеряемой среды.
Как правило, в качестве объемных единиц измерения количества среды используют: литр (л), кубический сантиметр (см³) и кубический метр (м³); а массовых — грамм (г), килограмм (кг) и тонну (т).
ХАРАКТЕРИСТИКИ ПОТОКА:
Наиболее важными характеристиками потока, влияющими на характер движения среды, являются:
Вязкостью (динамической) называют физическое свойство текучей среды, характеризующее внутреннее трение между ее слоями. Единицей измерения вязкости является Пуаз (П), вязкость маловязких жидкостей и газов измеряют в сотых долях Пуаза — сантипуазах (сП).
Наряду с динамической вязкостью используют величину, называемую кинематической вязкостью:
где ν — кинематическая вязкость;
µ — вязкость.
Единицей измерения кинематической вязкости служит Стокс (Ст), на практике чаще используется его сотая часть — сантистокс (сСТ).
Вязкость жидких сред с увеличением температуры уменьшается, причем для различных жидкостей данная зависимость различна. В то же время, вязкость жидких сред зависит и от давления, обычно возрастая при его увеличении. Однако, при давлениях, встречающихся в большинстве случаев (до 20 МПа), это изменение незначительно и, как правило, не учитывается.
Для газообразных сред зависимость вязкости от давления и от температуры весьма существенна: с увеличением давления кинематическая вязкость газов уменьшается, а с увеличением температуры — увеличивается.
ДВИЖЕНИЕ ЖИДКОСТИ В ТРУБОПРОВОДЕ:
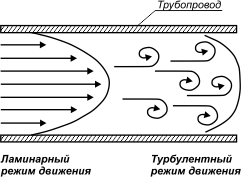
Скорость потока, вязкость и плотность жидкости определяют режим движения жидкости в трубопроводе. Исследование вопроса о механизме движения сред привело к заключению о существовании двух режимов движения жидкости:
Критерием оценки обоих режимов является число Рейнольдса:
Re = (V • D • ρ)/µ = (V • D)/ν,
где Re — число Рейнольдса;
D — внутренний диаметр трубопровода.
Ламинарный режим движения наблюдается при Re 4000, хотя данное значение, в зависимости от условий движения потока, может оказаться большим. Режим движения при 2000 При турбулентном же режиме эпюра скоростей имеет более сглаженный характер. Закон распределения скорости по сечению трубопровода играет важную роль при определении действительного расхода среды. Так как данный закон в большинстве случаев неизвестен, используется определение средней скорости потока — скорость, с которой должны двигаться через поперечное сечение потока все частицы, чтобы расход среды был равен расходу, полученному с действительными неодинаковыми для различных частиц скоростями.
В зависимости от принципа измерения, осреднение скорости потока производится либо конструктивным путем, либо вытекает из самого принципа измерения. «Качество» осреднения скорости потока напрямую влияет на точность работы расходомера.
При прохождении потока среды через местные сопротивления (колена, тройники, клапаны ) нарушается распределение скорости потока по сечению трубопровода (поток дестабилизируется). Поэтому, как правило, после местных сопротивлений перед расходомером необходимо выдержать прямой участок для стабилизации потока, в противном случае погрешность измерений может увеличиться. Как правило, для современных расходомеров прямой участок «до» составляет порядка 5…20 DN. Более детальные данные о величине прямых участков приводятся в техническом описании конкретного прибора.
Что такое расход в гидравлике
Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.
если угол в радианах, или
Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.
Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени
Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным
Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q1=Q2= const, откуда
Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).
Потерянная энергия или потерянный напор обозначаются 
Уравнение Бернулли для реальной жидкости будет иметь вид:
Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).
Потерянная высота 
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Выражение, стоящее перед 
Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.