Что такое распределительное переместительное сочетательное распределительное
Законы умножения
Переместительный закон умножения
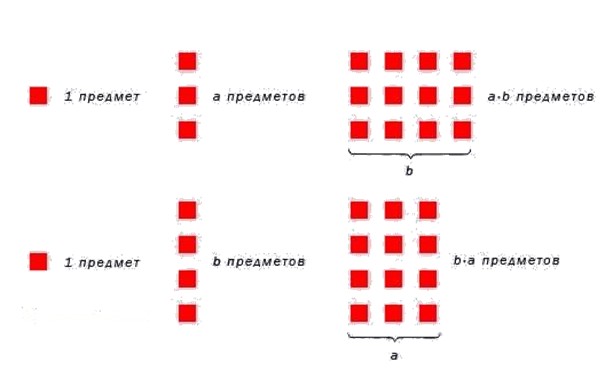
Если множимое и множитель поменять местами, то произведение не изменится. Это можно легко проверить при подсчёте двумя способами числа звёздочек представленных на рисунке:
3 + 3 + 3 + 3 = 4 + 4 + 4
Так как множимое и множитель можно менять местами их ещё называют сомножителями или просто множителями.
Таким образом, для любых натуральных чисел a и b верно равенство:
выражающее переместительный закон умножения:
От перестановки сомножителей произведение не меняется.
Сочетательный закон умножения
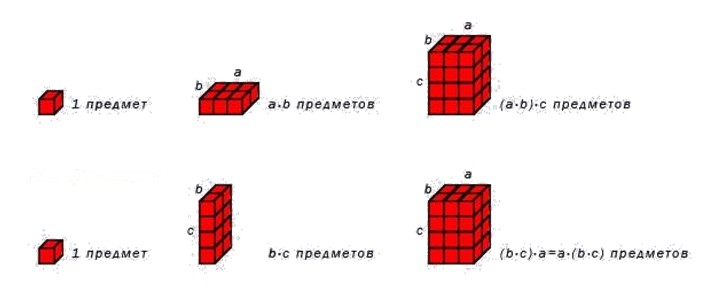
Произведение чисел 3, 2 и 4 не изменится, если из них какие-нибудь два числа заменить их произведением:
3 · 2 · 4 = 3 · (2 · 4) = 3 · 8 = 24,
3 · 2 · 4 = (3 · 2) · 4 = 6 · 4 = 24.
Таким образом, для любых натуральных чисел a, b и c верно равенство:
выражающее сочетательный закон умножения:
Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.
Распределительный закон умножения
Для любых натуральных чисел верны равенства:
выражающие распределительный закон умножения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на число и полученные произведения сложить.
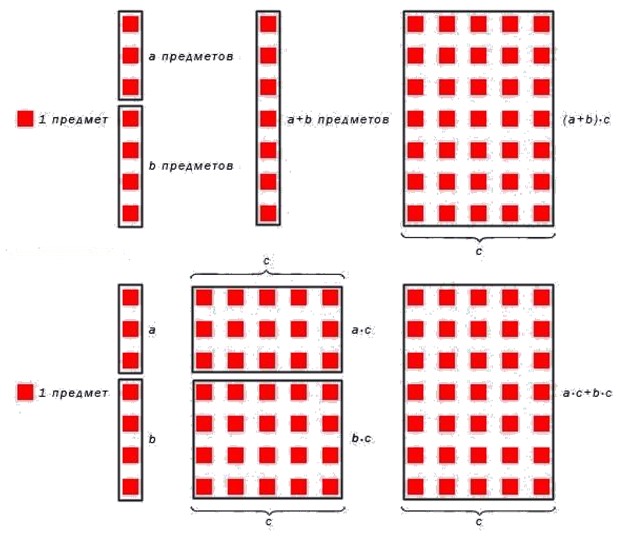
Распределительный закон умножения можно легко проверить при подсчёте двумя способами числа звёздочек, представленных на рисунке:
Первый: в каждом ряду расположено 3 жёлтых и 5 зелёных звёздочек, то есть всего в каждом ряду (3 + 5) звёздочек. В четырёх рядах всего (3 + 5) · 4 звёздочек.
Второй: жёлтые звёздочки расположены в четыре ряда по 3 звёздочки в каждом, то есть всего жёлтых звёздочек 3 · 4, а зелёных — 5 · 4. Всего звёздочек 3 · 4 + 5 · 4.
Кроме того, для любых натуральных чисел (если уменьшаемое больше или равно вычитаемому) верны равенства:
Переход от умножения:
соответственно к сложению и вычитанию:
называется раскрытием скобок.
Переход от сложения и вычитания:
называется вынесением общего множителя за скобки.
Сочетательное и распределительное свойства умножения
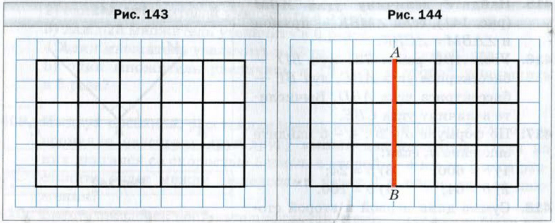
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143 ). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * ( 3 * 4 ).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
В буквенном виде это свойство записывают так:
(ab)c = a(bc)
Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
17 * 2 * 3 * 5 = ( 17 * 3 ) * ( 2 * 5 ).
На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
Равенсто 3 * ( 3 + 2 ) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
Это равенство позволяет формулу P = 2 a + 2 b для нахождения периметра прямоугольника записать в таком виде:
Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b − c) = ab − ac
1 ) Используем переместительное, а затме сочетательное свойства умножения:
1 ) Используя переместительное и сочетательное свойства умножения, получаем:
4 a * 3 b = ( 4 * 3 ) * ab = 12 ab.
2 ) Используя распределительное свойство умножения относительно вычитания, получаем:
18 m − 13 m = m( 18 − 13 ) = m * 5 = 5 m.
Согласно распределительному свойству умножения относительно сложения имеем:
Такое преобразование называют раскрытием скобок.
3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.
При решении примера было использовано распределительное свойство умножения относительно сложения:
3 сут 18 ч * 6 = ( 3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.
Переместительный, сочетательный и распределительный законы арифметики
Существует несколько законов, таких как: переместительный закон сложения и умножения, сочетательный закон сложения и умножения, распределительный закон умножения.
Переместительный закон сложения
От перемены мест слагаемых их сумма не изменится.
2 + 5 = 5 + 2
Так как 2 + 5 = 7 и 5 + 2 = 7
7 = 7
Сочетательный закон сложения
Как ни группируй слагаемые, значение суммы не изменится.
(12 + 6) + 11 = 12 + (6 + 11)
(12 + 6) +11 = 18 + 11 = 29 и 12 + (6 + 11) = 12 + 18 = 29
29 = 29
Переместительный закон сложения
От перемены мест множителей их произведение не меняется.
3 * 7 = 7 * 3
3 * 7 = 21 и 7 * 3 = 21
21 = 21
Сочетательный закон умножения
При любой группировки множителей их произведение не изменится.
(7 * 3) * 6 = 7 * (3 * 6)
(7 * 3) * 6 = 21 * 6 = 126
7 * (3 * 6) = 7 * 18 = 126
Распределительный закон умножения
Для умножения суммы на число можно по очереди умножить каждое слагаемое на это число, так называемым «фонтанчиком».
5 * (6 + 7) = 5 * 6 + 5 * 7
5 * (6 + 7) = 5 * 13 = 65
5 * 6 + 5 * 7 = 30 + 35 = 65
Умножение натуральных чисел: свойства, примеры
Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.
Переместительное свойство умножения натуральных чисел
Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:
Переместительный закон умножения
От перемены мест множителей произведение не меняется.
В буквенном виде переместительное свойство записывается так: a · b = b · a
На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.
Сочетательное свойство умножения натуральных чисел
Сочетательный закон умножения
Приведем формулировку в буквенном виде:
4 · 3 · 2 = 4 · 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24
4 · 3 · 2 = 12 · 2 = 12 + 12 = 24
Как видим, теория совпадает с практикой, и свойство справедливо.
Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.
Распределительное свойство относительно умножения
Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.
Распределительное свойство умножения относительно сложения
Запишем в форме буквенного выражения:
a · b + c = a · b + a · c
4 · 3 + 2 = 4 · 3 + 4 · 2 = 12 + 8 = 20
Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.
Распределительное свойство умножения относительно вычитания
Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.
Распределительное свойство умножения относительно вычитания
Запишем в форме буквенного выражения:
В предыдущем примере заменим «плюс» на «минус» и запишем:
Умножение единицы на натуральное число
Умножение единицы на любое натуральное число в результате дает данное число.
По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.
Умножение нуля на натуральное число
Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.
Умножение нуля на натуральное число
По определению, произведение 0 · a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.
В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.
Напимер: 0 · 498 = 0 ; 0 · 9638854785885 = 0
Свойства умножения и деления
Свойства умножения
Переместительное свойство умножения
От перестановки множителей произведение не меняется.
Сочетательное свойство умножения
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Переместительное и сочетательное свойства умножения позволяют сформулировать правило преобразования произведений.
При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.
Это свойство справедливо для любого количества слагаемых.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.
В буквенном виде свойство записывается так:
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Свойства деления
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
, где « k » — любое натуральное число.
Обратите внимание, что именно свойство деления выше позволяет нам сокращать дроби.
Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений.