Что такое равносильные неравенства

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №19. Равносильные уравнения и неравенства

Перечень вопросов, рассматриваемых в теме

1) понятие равносильного уравнения;

2) понятие равносильного неравенства;

3) понятие уравнения-следствия;

4) основные теоремы равносильности.

Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называет следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнения называется следствием первого уравнения.

Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Определение. Два уравнения с одной переменной

f(х) = g(х) и р(х) = h(х) называют равносильными, если множества их корней совпадают.

Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

1) Уравнения равносильны, т.к. каждое из них имеет только один корень х=3.

2) Уравнения также равносильны, т.к. у них одни и те же корни .

3) А вот уравнения не равносильны, потому что у первого уравнения корень х=2, а у второго уравнения два корня х=2 и х=-2.

Из определения равносильности следует, что два уравнения равносильны, если каждый корень первого уравнения является корнем второго уравнения, и наоборот.

Решение уравнения осуществляется в три этапа.

Второй этап — анализ решения. На этом этапе, анализируя проведенные преобразования, отвечают на вопрос, все ли они были равносильными.

Третий этап — проверка. Если анализ, проведенный на втором этапе, показывает, что некоторые преобразования могли привести к уравнению-следствию, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.

Реализация этого плана связана с поисками ответов на четыре вопроса.

Из курса средней школы мы знаем, что можно сделать следующие преобразования уравнений: любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.

Обе части уравнения можно умножить или разделить на одной и то же число, не равное нулю.

Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называет следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнения называется следствием первого уравнения.

Из этого определения и определения равносильности уравнений следует, что:

При решении уравнений главное- не потерять корни, а наличие посторонних корней можно установить проверкой. Поэтому важно следить за тем, чтобы при преобразовании уравнения каждое следующее уравнение было следствием предыдущего.

Стоит отметить, что посторонние корни могут получиться при умножении обеих частей уравнения на выражение, содержащее неизвестное; а вот потеря корней может произойти при делении обеих частей уравнения на выражение, содержащее неизвестное.

Итак, сформулируем основные теоремы, которые используются при решении равносильных уравнений:

Определение. Областью определения уравнения f(х) = g(х) или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной х, при которых одновременно имеют смысл выражения

Теорема 1. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.

Теорема 2. Если обе части уравнения возвести в одну и туже нечетную степень, то получится уравнение, равносильное данному.

Теорема 3. Показательное уравнение (где а > 0, a≠1)

равносильно уравнению f(x) = g(х).

Теорема 4. Если обе части уравнения f(x) = g(х) умножить на одно и то же выражение h(х), которое:

а) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x) = g(х)

б) нигде в этой области не обращается в 0, то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному в его ОДЗ.

Следствием теоремы 4: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Теорема 5. Если обе части уравнения f(x)=g(х) неотрицательны в ОДЗ уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение равносильное данному в его ОДЗ.

Краткая запись теорем 4, 5.

4. f(x) = g(x) ⇔h(x)f(x) = h(x)g(x), где h(x) ≠0

и h(x) имеет смысл в ОДЗ данного уравнения.

5. f(x) = g(x) ⇔ , где f(x)≥0, g(x)≥0

и n=2k (чётное число).

Например, х – 1 = 3; х = 4

Умножим обе части на (х – 2):

(х – 2)(х – 1) = 3(х – 2); х = 4 и х = 2 – посторонний корень⇒ проверка!

Равносильность неравенств с неизвестным определяется аналогично.

Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.

Разбор решения заданий тренировочного модуля

Решим уравнение:

Возведем в квадрат обе части уравнения, получим:

, которое не будет равносильно исходному уравнению, потому что у этого уравнения два корня , а у первоначального уравнения только один корень х=4.

Источник

Понятие равносильных неравенств и неравенств-следствий.

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Равносильными неравенствами называются неравенства, имеющие одни и те же решения или не имеющие таковых.

Другими словами, если каждое, отдельно взятое, решение первого неравенства является решением второго неравенства, а каждое, отдельно взятое, решение второго неравенства является решением первого, то такие неравенства равносильны.

б) каждое из неравенств не имеет решений. Значит, эти неравенства равносильны;

в) неравенства и не являются равносильными, так как второе неравенство в множестве своих решений содержит число 5, которое не является решением первого неравенства.

Равносильное преобразование неравенства – это замена его другим, равносильным ему неравенством, то есть, неравенством, имеющим то же множество решений. Сами преобразования, приводящие к равносильному неравенству, также называют равносильными преобразованиями.

Перечислим наиболее часто используемые равносильные преобразования неравенств.

Если выражения в левой и (или) правой части неравенства заменить тождественно равными выражениями на всей области определения исходного неравенства, то получится неравенство, равносильное данному.

Если к обеим частям неравенства прибавить (или отнять) одно и то же выражение, не изменяющее область определения исходного неравенства, то получится неравенство, равносильное данному.

Если какой-либо член неравенства перенести из одной части в другую с противоположным знаком, то получится неравенство равносильное исходному.

Если обе части неравенства умножить (разделить) на одно и то же выражение, положительное при всех значениях аргумента из области определения исходного неравенства, то получится неравенство, равносильное исходному.

Если обе части неравенства умножить (разделить) на одно и то же выражение, отрицательное при всех значениях аргумента из области определения исходного неравенства, и поменять знак неравенства на противоположный, то получится неравенство, равносильное исходному.

Если обе части неравенства возвести в одну и ту же нечётную степень, то получится неравенство, равносильное исходному.

Если обе части неравенства неотрицательны на всей области определения, то возведя обе части неравенства в одну и ту же чётную степень, получится неравенство, равносильное исходному.

Приведём несколько примеров применения равносильных преобразований при решении неравенств.

Если решение первого неравенства содержится в решении второго неравенства, то второе является следствием первого.

Итак, в завершение ещё раз обращаем внимание на то, что при решении неравенств необходимо совершать равносильные преобразования, во избежание появления посторонних решений или потери решений.

Источник

Равносильные неравенства, преобразование неравенств

В процессе решения неравенств зачастую происходит переход от заданного неравенства к неравенствам иного вида, имеющим то же решение, но определяемое проще. Иными словами, в результате преобразований заданное неравенство возможно заменить равносильным ему, облегчающим поиск решения. Данная статья посвящена способам равносильных преобразований. Сформулируем определение, рассмотрим основные виды преобразований.

Равносильные неравенства: определение, примеры

Равносильные неравенства – неравенства, имеющие одни и те же решения. В частном случае, неравенства, не имеющие решений, тоже называются равносильными.

Иными словами, если неравенства равносильны и имеют решения, то любое решение первого будет являться и решением второго. Ни одно из равносильных неравенств не имеет решений, не являющихся решениями других, равносильных ему неравенств.

Неравенства х > 3 и х ≥ 3 – не равносильные: х = 3 служит решением второго из этих равенств, но не служит решением первого.

Отметим, что указанное определение относится к неравенствам как с одной переменной, так и с двумя, тремя и более.

Равносильные преобразования неравенств

Возможно совершить некоторые действия с правой и левой частью неравенств, что даст возможность получать новые неравенства, имеющие решения, как и у исходного.

Равносильное преобразование неравенства – это замена исходного неравенства равносильным ему, т.е. таким, которое имеет то же множество решений. Сами действия-преобразования, приводящие к равносильному неравенству, тоже называют равносильными преобразованиями.

Равносильные преобразования дают возможность находить решения неравенств, преобразуя заданное неравенство в равносильное ему, но более простое и удобное для решения.

Рассмотрим основные виды равносильных преобразований: по сути без них не обходится решение ни одного неравенства. Отметим также, что равносильные преобразования неравенств очень похожи на равносильные преобразования уравнений. Схожи и принципы доказательства, только, конечно, в данном случае доказательства будут строиться на основе свойств числовых неравенств.

Итак, перечислим основные виды равносильных преобразований неравенств:

Подобные преобразования не должны сужать ОДЗ заданного неравенства, тогда возможно совершать тождественные преобразования обеих сторон неравенства.

Покажем пример использования.

Еще раз особенно укажем, как важен учет ОДЗ (область допустимых значений) при совершении замены частей неравенства тождественными выражениями. В случае, когда ОДЗ нового неравенства будет отлична от ОДЗ исходного, неравенство не может считаться равносильным. Это крайне важный аспект, пренебрежение им приводит к неверным ответам при решении неравенств.

Таким же образом приводится доказательство второй части утверждения. Здесь можно опереться на свойство умножения и деления числовых неравенств на отрицательное число при смене знака неравенства на противоположный.

Расширим и это свойство неравенств:

В целом, есть и другие равносильные преобразования, однако, они не так распространены и скорее имеют отношение к конкретному виду неравенств, например, к логарифмическим неравенствам. Познакомиться с ними можно подробнее в соответствующей теме.

Результат неравносильных преобразований неравенств

Сколь уж существуют равносильные преобразования, имеют место и неравносильные. Такие действия приводят к искажению заданного неравенства и дают в итоге решение, не являющееся истинным для исходного неравенства. Случается, что и при неравносильных преобразованиях получается верный ответ, но это не более чем случайность.

Собственно, вывод очевиден: решая неравенства, производить только равносильные преобразования.

Разберем примеры для лучшего понимания теории.

Пусть необходимо решить второе неравенство.

Посмотрим с другой стороны:

Неравносильные преобразования чаще всего происходят при невнимательном использовании свойств корней, логарифмов и модуля. Эти моменты будут детально рассмотрены в темах о решении неравенств соответствующих видов.

Источник

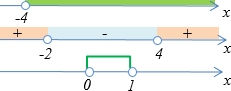
Что такое равносильные неравенства

В нашем задании большую роль будет играть понятие равносильности.

называются равносильными на множестве `X`, если каждое решение первого неравенства (уравнения), принадлежащее множеству `X`, является решением второго и, наоборот, каждое решение второго, принадлежащее `X`, является решением первого, или, если, ни одно из неравенств (уравнений) на `X` не имеет решений. Т. е. два неравенства (уравнения) равносильны, по определению, если множества решений этих неравенств (уравнений) на `X` совпадают.

Отсюда следует, что вместо того, чтобы решать данное неравенство (уравнение), можно решать любое другое, равносильное данному. Замену одного неравенства (уравнения) другим, равносильным данному на `X`, называют равносильным переходом на `X`. Равносильный переход обозначают двойной стрелкой `hArr`. Если уравнение `f(x) = 0` (или неравенство) `f(x) > 0`) равносильно уравнению `g(x) = 0` (или неравенству `g(x) > 0`), то это мы будем обозначать так:

`f(x) = 0 hArr g(x) = 0` (или `f(x) > 0 hArr g(x) > 0`).

При каких значениях параметра `a` системы

Решим сначала первую, более простую систему

Подставим `a = 3` во вторую систему

Следовательно, при `a = 3` системы равносильны, т. к. при этом значении параметра обе системы не имеют решений.

Итак, таких `a` три: `0, 1, 2`. Но при этих `a` вторая система может иметь и другие решения, а если у неё других решений нет, то её единственное решение может не совпадать с решением первой системы, и тогда такое `a` не удовлетворяет условию задачи. Проверим эти значения параметра.

2. `a=1`: Вторая система имеет вид

Следовательно, системы не равносильны, т. к. вторая имеет два решения.

Следовательно, системы при этом значении `a` равносильны – они имеют единственное решение `(4; 0)`.

Источник

40. Алгебра Читать 0 мин.

40.710. Равносильные системы

Два неравенства являются равносильными, если множества их решений совпадают. При решении неравенств иногда приходится переходить от одного неравенства к другому, более простому. Рассмотрим несколько равносильных переходов: для решения иррациональных, показательных, логарифмических неравенств, неравенств с модулем, дробно-рациональных неравенств.

1. Равносильные переходы для решения иррациональных неравенств

Для избавления от радикалов в иррациональных неравенствах требуется умение возводить обе части неравенства в соответствующую степень. Однако нужно быть осторожными при возведении в четную степень, если хотя бы одна из частей неравенства отрицательная. Неосторожное возведение в квадрат неравенства может повлечь за собой приобретение или потерю решений.

Пример. Решите неравенство

Решение. Применим равносильный переход:

Встречаются такие неравенства, в которых корень сравнивают с выражением. Тогда тоже пользуемся возведением в квадрат для избавления от иррациональности, однако, накладываем дополнительное ограничение – неотрицательность выражения, поскольку значение корня четной степени – число неотрицательное.

Пример. Решите неравенство

Воспользуемся равносильным переходом.

Решение. Воспользуемся равносильным переходом:

Если неизвестная входит как в основание, так и в показатель степени, то заранее неизвестно, будет ли основание степени больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая. Если неравенство строгое, то получаем следующий равносильный переход:

$(\phi (x))^ &gt (\phi (x))^\Leftrightarrow \left[ \begin \left\< \begin f(x)>g(x) \\ \phi (x) &gt 1 \end \right. \\ \left\< \begin f(x) &lt g(x) \\ 0 &lt \phi (x) (x+5)^<4>$

Используем следующий равносильный переход:

Если неравенство нестрогое, то нужно дополнительно рассмотреть случай – основание равно единице, т.к. тогда получается, что единица в любой степени равна единице, неравенство выполнится. Т.е. получаем следующий равносильный переход:

Используем следующий равносильный переход:

3. Равносильные переходы для решения логарифмических неравенств

Метод решений простейших логарифмических неравенств опирается на монотонность логарифмической функции, т.е. на правило отбрасывания логарифмов. Однако есть отличие от аналогичного правила отбрасывания оснований, которое объясняется тем, что при отбрасывании логарифмов расширяется ОДЗ неравенства. Значит, выражения, стоящие под логарифмами после отбрасывания последних могут стать отрицательными или равными нулю, следовательно, мы должны дополнительно учесть, что подлогарифмическое выражение положительно.

Если неизвестная входит как в основание, так и под знак логарифма, то заранее неизвестно, будет ли основание больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая.

Воспользуемся равносильным переходом:

Решением первой системы является интервал (0;0,5)

При решении неравенств второй системы видим, что пересечений решений нет.

Таким образом, решением совокупности является интервал (0;0,5)

Пример. Решите неравенство

Воспользуемся равносильным переходом:

При нанесении решений каждого неравенства системы на числовую прямую видим, что пересечений решений нет. Значит, неравенство не имеет решений.

4. Равносильные переходы для решения неравенств, содержащих знак модуля

Если модуль меньше функции, то избавляемся от модуля, но взамен получаем систему из двух неравенств. Учитываем случаи: если число под модулем положительно и если число под модулем отрицательно:

Решение. Воспользуемся равносильным переходом:

Рассмотренный пример наглядно демонстрирует, что метод работает всегда. Мы помним, что модуль числа по определению является величиной неотрицательной. В примере модуль меньше отрицательного числа, очевидно, что такое неравенство не имеет решений.

Пример. Решите неравенство

$\left\vert x+4\right\vert &lt 2x$

Воспользуемся равносильным переходом.

Решением системы является луч (4;∞).

Пример. Решите неравенство

$\left\vert x+2\right\vert \leq 5x$

Воспользуемся равносильным переходом.

Решением системы является луч (0,5;∞).

Если модуль больше выражения, то здесь иной равносильный переход.

Другими словами, мы рассматриваем два случая: 1) сначала просто игнорируем модуль — решаем обычное неравенство; 2) затем по сути раскрываем модуль со знаком «минус», а затем умножаем обе части неравенства на −1, меня при этом знак. При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.

Пример. Решите неравенство

$\left\vert x-7\right\vert >8x$

Воспользуемся равносильным переходом.

Решением совокупности является луч (-∞;1).

Пример. Решите неравенство

$\left\vert 2x+8\right\vert \geq x-5$

Воспользуемся равносильным переходом.

Решением совокупности является луч все множество действительных значений

5. Метод расщепления неравенств

То есть иными словами, дробь положительна, когда числитель и знаменатель одного знака; дробь отрицательна, когда числитель и знаменатель разных знаков.

Произведение двух множителей равносильно совокупности систем:

То есть иными словами, произведение двух множителей положительно, когда оба множителя одного знака; произведение отрицательно, когда оба множителя разных знаков.

Решение. Воспользуемся равносильным переходом.

Решение первой системы – луч [15;∞)

Решение второй системы – открытый луч (-∞;4).

Решение. Воспользуемся равносильным переходом.

Решение первой системы – полуинтервал (1;1,5]

Вторая система не имеет решений.

Источник