Что такое самосопряженный оператор

Сопряженные и самосопряженные преобразования
(операторы) евклидова пространства

Свойства сопряженного преобразования (оператора)

1. Сопряженное преобразование (оператор) — линейное.

2. Для каждого линейного преобразования существует единственное сопряженное преобразование, причем матрица сопряженного преобразования (в любом ортонормированном базисе) является транспонированной по отношению к матрице данного преобразования (в том же базисе).

Самосопряженные преобразования (операторы) евклидова пространства

Свойства самосопряженного преобразования

2. Все корни характеристического уравнения самосопряженного преобразования действительные.

В самом деле, предположим противное, а именно существование пары комплексных сопряженных корней [math]\lambda=\alpha\pm\beta i,

Найдем скалярные произведения:

3. Собственные векторы, принадлежащие различным собственным значениям самосопряженного преобразования, ортогональны.

Это следует из свойства 3 сопряженных преобразований (см. выше).

Положительные и неотрицательные преобразования евклидовых пространств

Отметим следующие свойства положительных и неотрицательных преобразований (операторов).

1. Из теоремы 9.10 следует, что для любой действительной симметрической матрицы [math]A[/math] существует диагональная матрица [math]\Lambda= \operatorname (\lambda_1,\ldots, \lambda_n)[/math] (с собственными числами матрицы [math]A[/math] на главной диагонали) и ортогональная матрица [math]S

3. Теорема 9.11 справедлива для любого линейного преобразования, если условие положительности самосопряженного преобразования заменить условием его неотрицательности.

4. Геометрический смысл теоремы 9.11 следующий: любое невырожденное линейное преобразование можно представить как композицию преобразований, каждое из которых есть либо простое отражение (относительно гиперплоскости), либо простой поворот (двумерной плоскости), либо растяжение вдоль взаимно перпендикулярных направлений.

Приведение самосопряженного преобразования (оператора) к диагональному виду

Нахождение диагонального вида матрицы самосопряженного преобразования ( первый этап ).

2. Составить искомую диагональную матрицу (9.22):

Нахождение матрицы [math]S[/math] перехода от данного базиса [math](\boldsymbol)[/math] к каноническому базису [math](\boldsymbol)[/math] ( второй этап ).

Первый этап. Находим диагональный вид матрицы преобразования.

1. При решении примера 9.2 были найдены корни характеристического уравнения [math]\lambda_1=0[/math] (кратности [math]n_1=2[/math] ) и [math]\lambda_2=3[/math] (кратности [math]n_2=1[/math] ).

4(1). Полученные столбцы записываем в искомую матрицу (звездочкой обозначены неизвестные пока элементы матрицы):

4(2). Полученный столбец дописываем в матрицу, полученную в пункте 4(1),

Матрица перехода к каноническому базису найдена.

Источник

Самосопряженный оператор

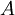
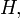
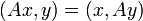
Эрмитов (самосопряжённый) оператор — оператор в комплексном гильбертовом пространстве удовлетворяющий равенству , где (х, у) — скалярное произведение в H.

Спектр (множество собственных чисел) самосопряжённого оператора является вещественным.

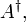
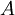
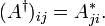
В конечномерных пространствах матрица самосопряжённого оператора является эрмитовой. Матрицей, эрмитово сопряжённой к данной, называют матрицу получаемую из исходной матрицы путем её транспонирования и перехода к комплексно сопряжённой, то есть Матрицу, равную своему эрмитовому сопряжению, называют эрмитовой, или самосопряжённой:

Собственные числа эрмитовой матрицы вещественны. У неё всегда существует ортонормированный базис из собственных векторов, собственные векторы, соответствующие различным собственным значениям, ортогональны.

Название дано в честь Шарля Эрмита, французского математика.

Эрмитовы операторы играют важную роль в квантовой механике, где с их помощью представляют наблюдаемые физические величины, см. Принцип неопределённости Гейзенберга.

См. также

Полезное

Смотреть что такое «Самосопряженный оператор» в других словарях:

САМОСОПРЯЖЕННЫЙ ОПЕРАТОР — см. Эрмитов оператор. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

САМОСОПРЯЖЕННЫЙ ОПЕРАТОР — э р м и т о в о п е р а т о р, линейный оператор А, определенный на линейном всюду плотном множестве D(А)гильбертова пространства Ни совпадающий со своим сопряженным оператором А, т … Математическая энциклопедия

НЕСАМОСОПРЯЖЕННЫЙ ОПЕРАТОР — линейный оператор в гильбертовом пространстве, спектральный анализ которого не укладывается в рамки теории самосопряженных операторов и ее простейших обобщений: теории унитарных операторов и теории нормальных операторов. Н. о. возникают при… … Математическая энциклопедия

ПОЛОЖИТЕЛЬНЫЙ ОПЕРАТОР — положительное отображение, 1) П. о. в гильбертовом пространстве линейный оператор А, для к рого соответствующая квадратичная форма ( Ах, х).неотрицательна. П. о. необходимо симметричен и допускает самосопряженное расширение, также являющееся П. о … Математическая энциклопедия

ИЗОМЕТРИЧЕСКИЙ ОПЕРАТОР — отображение Uметрич. пространства (X,rX). в метрич. пространство (Y, rY). такое, что для любых Если Xи Y действительные линейные нормированные пространства, U(X)=Y и U(0)=0, то U линейный оператор. И. о. Uотображает Xна U(X)взаимно однозначно,… … Математическая энциклопедия

ЛИНЕЙНЫЙ ОПЕРАТОР — линейное преобразование, отображение между двумя векторными пространствами, согласованное с их линейными структурами. Точнее, отображение где Еи F векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если при всех… … Математическая энциклопедия

Положительный оператор — Термин Положительный оператор в Теории операторов употребляется в двух различных смыслах. Под положительным оператором между векторными решетками понимают линейный оператор, переводящий положительные вектора в положительные. Самосопряженный… … Википедия

Источник

103. Самосопряженные операторы

Определение 1. Линейный оператор A евклидова пространства E называется Самосопряженным или симметричным, если A = A*, т. е. для любых векторов двух A, B €E выполняется условие:

Теорема 1. Линейный оператор A евклидова пространства E самосопряжен тогда и только, когда матрица A линейного оператора A в ортогональном базисе симметрическая матрица, т. е. A = A*.

Доказательство. По определению, оператор A самосопряжен тогда и только тогда, когда A = A*.

Линейные операторы A, A* Однозначно определяются своими матрицами A И A*. Тогда оператор A самосопряжен тогда и только тогда, когда A = A*. В силу теоремы 2 в ортонормированном базисе это равносильно условию A = At, т. е. симметричности матрицы A. 

Теорема 2. Все корни характеристического уравнения самосопряженного оператора A — действительные числа и поэтому являются собственными значениями линейного оператора.

. (2)

. Покажем, что. Обозначим При транспонировании квадратная матрица порядка 1 не меняется и мы имеем

С другой стороны, переходя к сопряженным числам, получаем

Так как симметрическая матрица с действительными элементам, то Поэтому И Y€R. Так как число неравно нулю, то из равенства (2) находим, что l0€R. Получаем противоречие. Следовательно, все корни характеристического уравнения действительные числа.

Теорема 3. Собственные векторы самосопряженного оператора A, соответствующие различным собственным значениям ортогональны.

Определение 2. Подпространство L евклидово пространство E называется Инвариантным относительно линейного оператора A, если образ L при отображении A Лежит в L, т. е. A(L^) Í L^.

Теорема 4. Если подпространство L инвариантно относительно самосопряженного оператора A, то и ортогональное дополнение L^ инвариантно относительно A.

Теорема 5. Пусть A — самосопряженный линейный оператор, действующий в N-мерном евклидовом пространстве E. Тогда в E существует ортонормированный базис, состоящий из собственных векторов оператора A.

Доказательство. Теорему доказываем методом математической индукцией по размерности N. Если N = 1, то каждый вектор собственный в и в качестве требуемого базиса возьмем любой вектор единичной длины из E.

Источник

Что такое самосопряженный оператор

Индивидуальные онлайн уроки: Отправьте запрос сейчас: ut2018@protonmail.com
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Линейные самосопряженные операторы Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

1. Понятие сопряженного оператора. Мы будем рассматривать линейные операторы в конечномерном евклидовом пространстве V. Определение 1. Оператор А* из L(V, V) называется сопряженным к линейному оператору А, если для любых х и у из V выполняется соотношение

(Ах, у) = (х, А*у). (5.51)

Легко убедиться в том, что оператор А*, сопряженный к линейному оператору А, сам является линейным оператором. Это вытекает из очевидного соотношения

справедливого для любых элементов х, у₁, у₂ и любых комплексных чисел α и β.

Докажем следующую теорему.

Теорема 5.12. Каждый линейный оператор А имеет единственный сопряженный.

Доказательство. Очевидно, скалярное произведение (Ах, у) представляет собой полуторалинейную форму (см. гл. 4, § 3, п. 1 и определение полуторалинейной формы). По теореме 5.11 существует единственный линейный оператор А* такой, что эта форма может быть представлена в виде (х, А*у). Таким образом, (Ах, у) = х, А*у.
Следовательно, оператор А* — сопряженный к оператору А. Единственность оператора А* следует из единственности представления полуторалинейного оператора в виде E.44). Теорема доказана.

В дальнейшем символ А* будет обозначать оператор, сопряженный к оператору А.
Отметим следующие свойства сопряженных операторов:

Доказательства свойств 1°-4° элементарны, и мы предоставляем их читателю. Приведем доказательство свойства 5°. Согласно определению произведения операторов справедливо соотношение (АВ)х = А(Вх). С помощью этого равенства и определения сопряженного оператора получаем следующую цепочку соотношений:

((АВ)х, у) = (А(Вх), у) = (Вх, А*у) = = (х, В*(А*у)) = (х, (В*А*)у).

Таким образом, ((АВ)х, у) = (х, (В*А*)у). Иными словами, оператор В*А* является сопряженным к оператору АВ. Справедливость свойства 5° установлена.

Замечание. Понятие сопряженного оператора для вещественного пространства вводится совершенно аналогично. Выводы этого пункта и свойства сопряженных операторов справедливы и для этого случая (при этом свойство 3° формулируется так: (λА)* = λА*).

2. Самосопряженные операторы. Основные свойства.
Определение 2. Линейный оператор А из L(V, V) называется самосопряженным, если справедливо равенство

Самосопряженный оператор в вещественном пространстве определяется аналогично.
Простейшим примером самосопряженного оператора является тождественный оператор I (см. свойство 1° сопряженных операторов в предыдущем пункте).
С помощью самосопряженных операторов можно получить специальное представление произвольных линейных операторов. Именно, справедливо следующее утверждение.

Теорема 5.13. Пусть А — линейный оператор, действующий в комплексном евклидовом пространстве V. Тогда справедливо представление А = А_R + iА_I, где А_R и А_I — самосопряженные операторы, называемые соответственно действительной и мнимой частью оператора А.

Очевидно, А = А_R + iА_I Теорема доказана.

В следующей теореме выясняются условия самосопряженности произведения самосопряженных операторов. Мы будем говорить, что операторы А и В коммутируют, если АВ = ВА.

Теорема 5.14. Для того чтобы произведение АВ самосопряженных операторов А и В было самосопряженным оператором, необходимо и достаточно, чтобы они коммутировали.
Доказательство. Так как А и В — самосопряженные операторы, то, согласно свойству 5° сопряженных операторов (см. п. 1 этого параграфа), справедливы соотношения
(АВ)* = В*А* = ВА (5.52)

Следовательно, если АВ = ВА, то (АВ)* = АВ, т.е. оператор АВ — самосопряженный. Если же АВ —самосопряженный оператор, то АВ = (АВ)*, и тогда, на основании (5.52), АВ = ВА. Теорема доказана.
В дальнейших теоремах устанавливается ряд важных свойств самосопряженных операторов.
Теорема 5.15. Если оператор А самосопряженный, то для любого х ϵ V скалярное произведение (Ах, х) — вещественное число.
Доказательство. Справедливость утверждения теоремы вытекает из следующего свойства скалярного произведения в комплексном евклидовом пространстве и определения самосопряженного оператора (Напомним, что если комплексное число равно своему сопряженному, то
это число — вещественное.)

Теорема 5.16. Собственные значения самосопряженного оператора вещественны.
Доказательство. Пусть λ — собственное значение самосопряженного оператора А. По определению собственного значения оператора А (см. определение 2 § 3 этой главы) существует ненулевой вектор х
такой, что Ах = λх. Из этого соотношения следует, что вещественное (в силу теоремы 5.15) скалярное произведение (Ах, х) может быть представлено в виде 2 )

( 2) Напомним, что символ ||х|| обозначает норму элемента х. )

Так как ||х|| и (Ах, х) вещественны, то, очевидно, и λ — вещественное число. Теорема доказана.

В следующей теореме выясняется свойство ортогональности собственных векторов самосопряженного оператора.
Теорема 5.17. Если А — самосопряженный оператор, то собственные векторы, отвечающие различным собственным значениям этого оператора, ортогональны.

3) Так как собственные значения самосопряженного оператора вещественны, то

Так как оператор А самосопряженный, то скалярные произведения (Ax₁, х₂) и (x₁, Aх₂) равны, и поэтому из последних соотношений путем вычитания получаем равенство

Поскольку λ₁ ≠ λ₂ то из последнего равенства следует равенство нулю скалярного произведения (x_1*х₂ ), т.е. ортогональность собственных векторов x₁ и х₂ Теорема доказана.

3. Норма линейного оператора. Пусть А — линейный оператор, отображающий евклидово пространство V в это же пространство. Введем понятие нормы оператора А.
Определение 3. Нормой ||A|| линейного оператора А называется число, определяемое соотношением 1 )

1 ) Напомним, что Отсюда следует, что представляет собой непрерывную функцию х, которая на замкнутом множестве ||х|| = 1 достигает конечного наибольшего значения.

Из определения нормы линейного оператора вытекает следующее очевидное неравенство:

(для доказательства достаточно воспользоваться соотношением Ах =

Из соотношения E.54) следует, что если ||А|| = О, то оператор А является нулевым.

Норму самосопряженного оператора А можно определить и другим способом. Именно, справедливо утверждение:

Если А — самосопряженный оператор, то введенная выше норма ||А|| оператора А равна

Доказательство. Для любого х из V справедливо неравенство Коши-Буняковского (см. п. 2 §3 гл.4)

Из него и из неравенства (5.54) получаем следующее неравенство:

Отметим, что из равенства

и определения числа μ (см. 5.56)) вытекает следующее неравенство:

Обратимся теперь к следующему очевидному тождеству:

(в этом тождестве символ Re (Ax, у) обозначает действительную часть комплексного числа (Ах, у), само тождество легко вытекает из свойств скалярного произведения, см. п. 1 §3 гл.4). Беря левую и правую
части этого тождества по модулю, используя свойство модуля суммы и неравенство E.58), получим следующие соотношения 1 ) :

1 ) Мы использовали при этом определение нормы элемента в комплексном евклидовом пространстве.

Отсюда при ||х|| = ||у|| = 1 получаем неравенство

Полагая в этом неравенстве (очевидно, ||у|| = 1) и учитывая, что число (Ах, Ах) = ||Ах|| 2 является вещественным (поэтому получим

Отсюда, согласно неравенству (5.53), найдем

Для завершения доказательства остается сравнить полученное неравенство с неравенством (5.57) и воспользоваться определением числа µ (см. 5.56)).

4. Дальнейшие свойства самосопряженных операторов. В этом пункте мы докажем ряд важных свойств линейных операторов, связанных с понятием нормы. Сначала мы установим необходимое и достаточное условие самосопряженности оператора. Докажем следующую теорему.
Теорема 5.18. Для того чтобы линейный оператор А был самосопряженным, необходимо и достаточно, чтобы 2 )

2 ) Символ Im (Ax, х) обозначает мнимую часть комплексного числа (Ах, х). Равенство Im (Ах, х) = 0 означает, что число (Ах, х) является вещественным.

Доказательство. По теореме 5.13 произвольный линейный оператор А может быть представлен в виде

самосопряженные операторы. Поэтому

причем, согласно теореме 5.15, для любого х числа и — вещественные. Следовательно, эти числа соответственно равны действительной и мнимой частям комплексного числа (Ах, х):

Допустим, что А — самосопряженный оператор. По теореме 5.15 в этом случае (Ах, х) — вещественное число,
и поэтому Im (Ax, х) = 0. Необходимость условия теоремы доказана.

Докажем достаточность условия теоремы.

Пусть Im(Ax, х) = (А_Iх, х) = 0. Отсюда следует, что ||А_I|| = 0, т. е. А_I = 0. Поэтому А = А_R, где А_R —самосопряженный оператор.
Теорема доказана.
В следующих утверждениях выясняются некоторые свойства собственных значений самосопряженных операторов.

Лемма. Любое собственное значение X произвольного линейного самосопряженного оператора А в евклидовом пространстве равно скалярному произведению (Ах, х), где х — некоторый вектор, удо-
влетворяющий условию ||х|| = 1:

Доказательство. Так как λ — собственное значение оператора А, то существует такой ненулевой вектор z, что

Полагая x = z/||z|| (очевидно, ||х|| = 1), перепишем 5.60) следующим образом: Ах = λ х, ||х|| = 1. Отсюда получаем соотношения т.е. 5.59) имеет место. Лемма доказана.
Cледствие. Пусть А — самосопряженный оператор и λ — любое собственное значение этого оператора. Пусть далее

Справедливы следующие неравенства:

Замечание 1. Так как скалярное произведение (Ах, х) представляет собой непрерывную функцию от х, то на замкнутом множестве ||х|| = 1 эта функция ограничена и достигает своих точных граней m и М.
Замечание 2. Согласно теореме 5.16 собственные значения самосопряженного оператора вещественны. Поэтому неравенства 5.62) имеют смысл.
Доказательство следствия. Так как любое собственное значение λ удовлетворяет соотношению (5.59), то, очевидно, каждое собственное значение заключено между точными гранями m и М скалярного произведения (Ах, х). Поэтому неравенства (5.62) справедливы.
Мы докажем, что числа т и М, определенные соотношениями (5.61) являются соответственно наименьшим и наибольшим собственными значениями самосопряженного оператора А. Предварительно убедимся в справедливости следующего утверждения.

Теорема 5.19. Пусть А — самосопряженный оператор и, кроме того, (Ах, х) ≥ О для любого х. Тогда норма ||А|| равна наибольшему собственному значению этого оператора 1 )

1 ) Так как собственных значений конечное число и они вещественны, то из них можно указать наибольшее.

Доказательство. Мы уже отмечали (см. утверждение предыдущего пункта), что

Так как (Ах, х) ≥ О, то Согласно замечанию 1 этого пункта для некоторого

Обращаясь к определению нормы и используя только что написанные равенства, получим соотношения 2 )

Таким образом, или, иначе, — собственное значение оператора А. То, что λ — наибольшее собственное значение, вытекает из только что установленного следствия из леммы этого пункта. Теорема доказана.

Докажем теперь, что числа m и М (см. 5.61)) являются наименьшим и наибольшим собственными значениями самосопряженного оператора А.

Теорема 5.20. Пусть А — самосопряженный оператор, а m и М — точные грани (Ах, х) на множестве ||х|| = 1. Эти числа представляют собой наименьшее и наибольшее собственные значения оператора А.
Доказательство. Очевидно, достаточно доказать, что числа m и М — собственные значения оператора А. Тогда из неравенств 5.62) сразу же следует, что т и М являются соответственно наименьшим и наибольшим собственными значениями.
Докажем сначала, что М — собственное значение. Для этого рассмотрим самосопряженный оператор В = А — mI. Так как

то оператор В удовлетворяет условиям теоремы 5.19, и поэтому норма ||В|| этого оператора равна наибольшему собственному значению. С другой стороны,

Таким образом, (М — m) — наибольшее собственное значение оператора В. Следовательно, существует такой ненулевой вектор х₀, что

Так как

Согласно только что проведенному доказательству число — m представляет собой собственное значение оператора В. Так как В = —А, то т будет являться собственным значением оператора А. Теорема доказана.

В следующей теореме выясняется важное свойство собственных векторов самосопряженного оператора.

Доказательство. Пусть λ₁ — максимальное собственное значение оператора

Обозначим через e₁ собственный вектор, отвечающий λ₁ и удовлетворяющий условию ||e₁|| = 1 (возможность его выбора следует из доказательства леммы этого пункта).
Обозначим через V₁ (n — 1)-мерное подпространство пространства V, ортогональное к е₁ Очевидно, V₁ — инвариантное подпространство оператора А (т. е. если х ϵ V₁, то и Ах ϵ V₁. Действительно, пусть х ϵ V₁ (т. е. (х,е₁=0). Тогда 1 )

1 ) Мы использовали свойство самосопряженности оператора (Ах, e ₁ ) = (х, Ае ₁ ) и то обстоятельство, что e ₁ — собственный вектор оператора:

1 ) Символ обозначает ортогональность векторов e₁ и e₂

Кроме того, можно указать такой вектор что

Замечание 2. Из рассуждений в доказательстве теоремы следует соотношение

Это соотношение можно также записать в виде

причем норма элемента х/||х|| равна 1.

Пусть ∑_m — множество всех m-мерных подпространств пространства V. Справедливо следующее важное минимаксное свойство собственных значений.
Теорема 5.22. Пусть А — самосопряженный оператор и — его собственные значения, занумерованные в порядке, указанном в замечании 1. Тогда

Поэтому для доказательства теоремы достаточно убедиться в справедливости соотношения

для любого

Перейдем к доказательству соотношения (5.65). Обозначим символом ортогональное дополнение подпространства Е (см. п.З §2 гл.4). Из теоремы 2.10 следует, что размерность равна n — m. Следовательно,

Это означает, в силу теоремы 2.9, что пересечение подпространств и E_m+1 содержит ненулевой элемент. Итак, существует элемент такой, что

Поскольку е_k, — собственные векторы оператора А, то из последних соотношений получаем

Отсюда и из ортонормированности е_k, следует справедливость соотношения

Мы занумеровали собственные значения в порядке убывания с уче т ом возможной их кратности. Поэтому

Отсюда и из соотношений 5.67) и 5.66) получаем

Замечая, что для любого х ≠ 0 норма элемента х/||х|| равна 1 и 1, а также учитывая, что , получим

Итак, соотношения (5.65) установлены. Теорема доказана.

5. Спектральное разложение самосопряженных операторов. Теорема Гамильтона-Кэли.

(см. п. 3 § 2 гл. 4), а так как то с помощью (5.68) получаем

Оператор Р_k, определяемый соотношением

называется проектором на одномерное подпространство, порожденное вектором е_k.
Из свойств скалярного произведения сразу же следует, что Р_k — самосопряженный линейный оператор.
Отметим следующие важные свойства проекторов:

Доказательство этих свойств следует из соотношений

Заметим также, что непосредственно из определения (5.70) следует, что Р_k, коммутирует с каждым оператором, который коммутирует с А. Из соотношений (5.68), (5.69) и (5.70) получаем следующие выражения для х и Ах:

Из равенства (5.71) следует, что оператор является тожд ественным

Из равенства (5.72) получаем так называемое спектральное разложение самосопряженного оператора:

Из свойств 1° и 2° проекторов и из соотношения (5.74) вытекает следующее выражение для А 2 :

Очевидно, вообще для любого целого положительного s

Рассмотрим произвольный полином По определению считают

Обращаясь к соотношению (5.75), легко получить следующее выражение для р(А):

Докажем следующую теорему.

Теорема 5.23 (теорема Гамильтона-Кэли). Если А — самосопря ж енный оператор и

характеристический многочлен этого оператора, то

Доказательство. Действительно, если А — самосопряженный оператор и λ_i — собственные значения этого оператора, то, согласно теореме 5.8, λ_i является корнем характеристического уравнения, т. е. p( λ_i ) = 0. Отсюда и из соотношения 5.76) следует, что р(А) = 0.
Теорема доказана.

6. Положительные операторы. Корни m-й степени из оператора.

Самосопряженный оператор А называется положительным, если
для любого х из V справедливо соотношение

Если оператор А — положительный и из условия (Ах, х) = 0 следует, что х = 0, то А называется положительно определенным оператором.

Положительные и положительно определенные операторы соответственно обозначаются символами А ≥ 0 и А > 0.
Отметим следующее простое утверждение.
Каждое собственное значение положительного (положительно определенного) оператора неотрицательно (положительно). Это утверждение следует из простых рассуждений. Пусть λ —собственное значение оператора А. Тогда, согласно лемме п. 4 этого параграфа, можно указать такой элемент х, ||х|| = 1, что λ = (Ах, х).
Отсюда и из соотношения (5.77) получаем, что А > 0 для положительных операторов и λ > 0 для положительно определенных операторов. Утверждение доказано.

Введем понятие корня m-й степени (m — натуральное число) из оператора.

Определение. Корнем m-й степени из оператора А называется оператор В такой, что В m = А.
Корень m- й степени из оператора А обозначается символом Естественно выделить какой-либо класс операторов, для которых имела бы смысл операция нахождения корня m-й степени. Определенный ответ на этот вопрос дается следующей теоремой.

Теорема 5.24. Пусть А — положительный самосопряженный оператор, А ≥ 0. Тогда для любого натурального m существует положительный самосопряженный оператор , ≥ 0.

Доказательство. Обозначим через λ_k собственные значения оператора А, и пусть <е_к> — ортонормированный базис из собственных векторов. Обозначим далее через Р_k проектор на одномерное подпространство, порожденное вектором е_k.
Согласно предыдущему пункту имеет место спектральное разложение (5.74) самосопряженного оператора А:

Так как λ_k ≥ 0 (см. только что доказанное утверждение), то можно ввести следующий самосопряженный оператор В:

Согласно (5.70) справедливо соотношение

из которого следует положительность операторов Р_к и положительность оператора В (см. 5.78)). Из свойств 1° и 2° проекторов Р_к (см. п. 5 этого параграфа) вытекает, что

Сравнивая это выражение для В m с выражением (5.74) для А, получим В m = А. Выше была установлена положительность оператора В. Теорема доказана.

Замечание 1. Отметим без доказательства, что существует единственный положительный оператор

Замечание 2. В ортонормированном базисе <е_k> собственных векторов оператора А матрица оператора

Источник