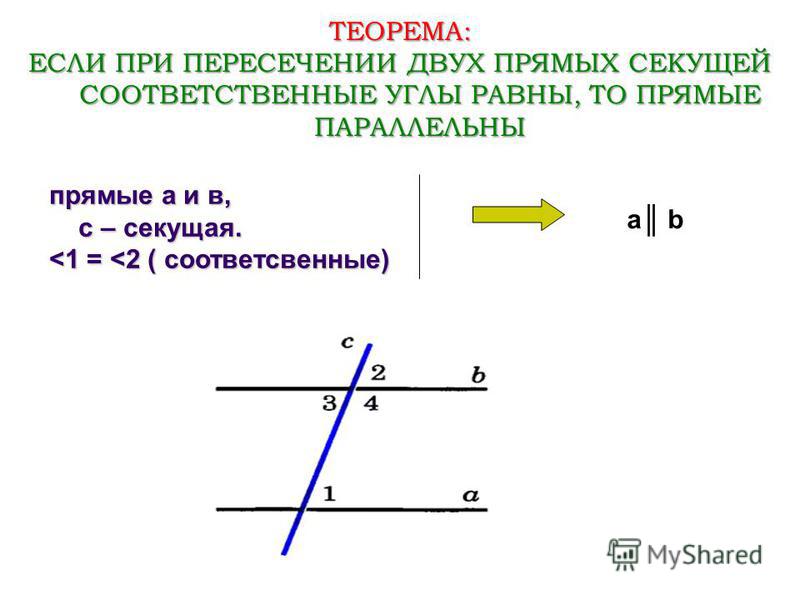
Что такое секущая прямая
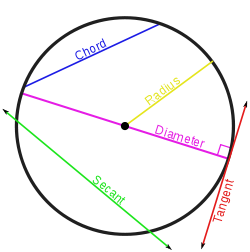
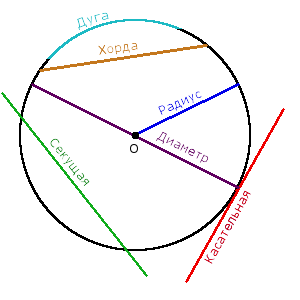
Хорда, секущая, касательная
Определения
Хорда – отрезок, соединяющий две точки окружности.
Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Свойства
Радиус, проведенный в точку касания, перпендикулярен касательной
Отрезки касательных, проведенных к окружности из одной точки, равны.
Отрезки пересекающихся хорд связаны соотношением:
Произведения отрезков секущих, проведенных из одной точки, равны:
Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки:
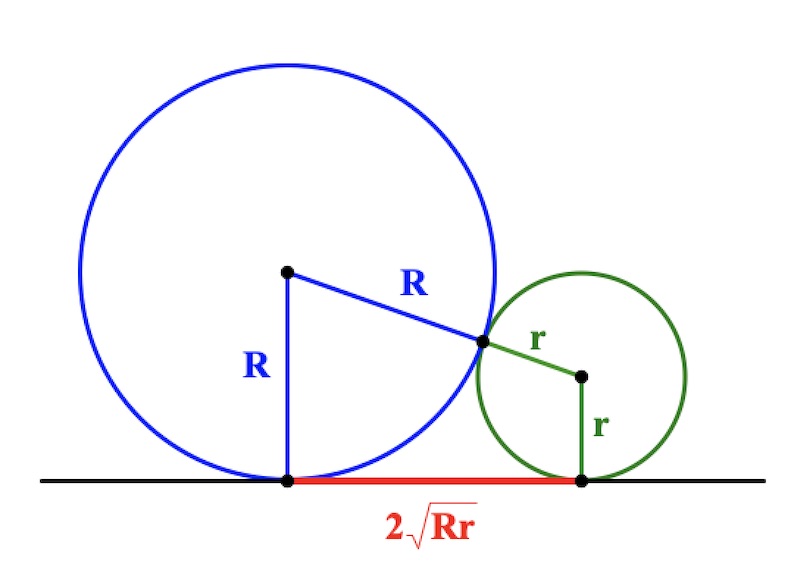
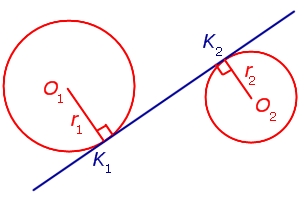
Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов Видеодоказательство
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Секущая прямая
Секущая — это прямая, которая на некотором участке пересекает в двух точках данную кривую.
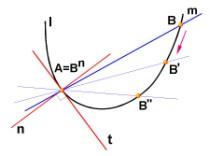
Путём приближения из секущей можно получить касательную в некоторой точке P. Если секущая определяется двумя точками пересечения с данной кривой, P и Q, где положение точки P фиксировано, а положение точки Q может изменяться, то по мере того, как точка Q приближается к точке P вдоль кривой, направление секущей приближается к направлению касательной в точке P (считаем, что первая производная кривой является непрерывной в точке P, и поэтому существует только одна касательная в этой точке). Можно сказать, что по мере того, как точка Q приближается к P, наклон секущей, или направление, в пределе приближается к наклону касательной. Эта идея является основой для геометрического определения производной.
Хорда — это участок секущей, который лежит между двумя точками пересечения с кривой.
См. также
Ссылки
Полезное
Смотреть что такое «Секущая прямая» в других словарях:
секущая — прямая Словарь русских синонимов. секущая сущ., кол во синонимов: 1 • прямая (6) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
прямая — биссектриса, параллель, линия, секущая, хорда, директриса Словарь русских синонимов. прямая сущ., кол во синонимов: 6 • биссектриса (3) • … Словарь синонимов
СЕКУЩАЯ — СЕКУЩАЯ, ей, жен. В математике: прямая, пересекающая кривую. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
СЕКУЩАЯ — всякая прямая, имеющая с кривой линией по меньшей мере две общие точки. Отрезок секущей, лежащий внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром … Большая политехническая энциклопедия
Секущая — ж. Прямая линия, пересекающая кривую в двух или более точках. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
секущая — ой; ж. Матем. Прямая, пересекающая кривую в двух или более точках … Энциклопедический словарь
секущая — ой; ж.; матем. Прямая, пересекающая кривую в двух или более точках … Словарь многих выражений
Секанс — [лат. secans, здесь секущая (прямая); от seco режу, рассекаю], одна из тригонометрических функций (См. Тригонометрические функции); обозначение sec. В прямоугольном треугольнике С. острого угла называют отношение гипотенузы к катету,… … Большая советская энциклопедия
СЕКАНС — [лат. secans, здесь: секущая (прямая), от seco режу, рассекаю] одна из тригонометрических функций … Большой энциклопедический политехнический словарь
Касательная — прямая, с которою стремится совпасть секущая, проведенная через две точки на произвольной кривой по мере сближения этих точек. Математическая теория К. имеет весьма важное значение (см. Дифференциальное исчисление). Точка, через которую к кривой… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Касательная и секущая к окружности
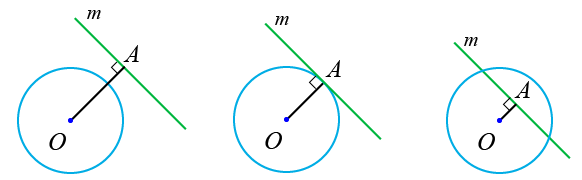
На плоскости прямая и окружность могут либо пересекаться друг с другом, либо не пересекаться:
Расстояние от центра O до прямой m равно длине перпендикуляра OA. Следовательно, расстояние от центра окружности до прямой всегда будет равно перпендикуляру, опущенному из центра окружности на прямую.
Если расстояние от центра окружности до прямой больше радиуса данной окружности, то прямая и окружность не пересекаются и не имеют общих точек:
Касательная
Если расстояние от центра окружности до прямой равно радиусу данной окружности, то прямая касается окружности и они имеют одну общую точку, такая прямая называется касательной к окружности:
Прямая m — касательная. Точка соприкосновения прямой и окружности, то есть их общая точка, называется точкой касания: точка A — точка касания.
Касательная – это прямая линия, имеющая с окружностью одну общую точку.
Секущая
Если расстояние от центра окружности до прямой меньше радиуса данной окружности, то прямая пересекает окружность и они имеют две точки касания, такая прямая называется секущей к окружности:
Секущая – это прямая линия, имеющая с окружностью две общие точки.
Секущая прямая
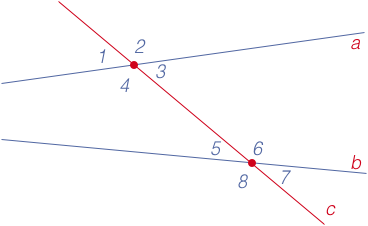
Секущая двух прямых
Согласно пятому постулату Евклида, две прямые параллельны, если:
Любой из этих признаков является необходимым и достаточным условием того, что прямые параллельны.
Касательные прямые к одной окружности
Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).
По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).
Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.
Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.
Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.
Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.
Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.
Геометрическое построение
Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.
Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.
Построение касательной прямой к окружности
Для построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.
Теорема об описанном четырёхугольнике и вписанные окружности
Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть
Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a.
Но каждая сторона четырёхугольника состоит из двух таких отрезков
что и доказывает утверждение.
Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.