Что такое сетевой граф

Основные понятия и определения сетевого графа

Сетевая модель – структурированное описание объекта управления через набор взаимосвязанных и взаимозависимых основных элементов, характеризуемых временными и стоимостными параметрами.

Основными элементами сетевой модели являются: работа, событие, продолжительность работы; величина ресурса, потребного для выполнения каждой из работ; различные пути достижения конечной цели, критический путь; резервы.

Сетевая модель может быть представлена в формализованной записи (символьное представление), в виде графа или в текстовом изложении.

Сетевой граф представляет собой сочетание вершин и дуг.

Далее рассмотрим вариант сетевого графа, представленного в терминах работ, когда вершинами являются события, а дугами – работы.

Событие – это результат выполнения всех входящих в него работ. После выполнения всех входящих в событие работ оно наступает мгновенно, поэтому продолжительность свершения события равна нулю. Событие обозначается кружком . При нумерации событий его

номер проставляется внутри кружка . Нумерация событий начинается с номера 1.

где — начальное событие, ;

– конечное событие, ;

– работа.

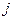
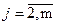
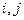
События i и j называются смежными событиями.

В сетевом графе различают несколько видов работы:

3) фиктивная (зависимость).

Под действительной работой понимается процесс, требующий затрат времени и ресурсов. Каждая работа характеризуется либо затратами труда (временные параметры), либо стоимостью ее выполнения (стоимостные параметры). Выполнение работы связано с необходимостью использования различных ресурсов, поэтому в числе характеристик каждой работы выступает также показатель количества источников ресурса (ресурсов), необходимых для выполнения конкретной работы. При этом может потребоваться один или несколько видов ресурсов. Количество этих видов ресурсов определяет сетевую модель как одноресурсную или многоресурсную. Действительная работа на сетевом графе отображается сплошной стрелкой , направленной от начального к конечному событию (не смешивать с исходным и завершающим событиями сетевого графа).

Например, необходимо произвести сборку станка, которая включает выполнение комплекса работ (технологических операций). Выполнение этих операций требует: привлечения рабочих (слесарей-сборщиков); подготовки площадки для выполнения операций сборки; специальных сборочных приспособлений; необходимого для сборки комплекта деталей, узлов и т.п., то есть трех источников ресурсов – живого труда, средств и предмета труда. Потребность в каждом из этих ресурсов определяется сложностью собираемого станка, особенностями выполнения операций сборки и т.д.

Все подготовительные и технологические операции сборки требуют соответствующих видов ресурсов, характеризуются определенной продолжительностью, следовательно, являются действительными работами. Эти работы взаимоувязаны. Работа, непосредственно предшествующая данной, называется непосредственно предшествующей работой, а непосредственно следующая за данной – непосредственно следующей; они характеризуются определенной взаимозависимостью – непосредственного предшествования или следования, а совокупность работ графа может быть либо предшествующей данной работе, либо следующей за ней. Таким образом, все работы могут быть представлены в виде сетевого графа.

Ожидание – это процесс, который требует только затрат времени и не нуждается в использовании ресурсов (например, процесс остывания детали после термообработки, затвердевание бетона и др.). Ожидание на графе также изображается сплошной линией .

«Фиктивная работа», или зависимость, отражает логическую связь между двумя или несколькими событиями. «Фиктивная работа» не требует для своего осуществления ни затрат времени, ни ресурсов. Этот вид работы указывает только на то, что определенное событие не может наступить, а работа не может начаться без наступления другого события или выполнения другой работы, непосредственно предшествующей данной.

Например, необходимо определить потребность организации в материальных ресурсах. Для такого расчета требуются производственная программа в разрезе выпускаемых наименований изделий и нормы расхода конкретного материала на то или иное изделие. Производственную программу для цехов организации формирует производственно-диспетчерский отдел, норму расхода материала устанавливает технологический отдел. Расчет потребности в материалах не может быть начат без получения соответствующей информации от указанных отделов организации, т.е. без завершения работ по указанным ранее расчетам. Таким образом, между расчетом потребности в материалах и формированием производственной программы и установлением норм расхода материалов существует зависимость – фиктивная работа. Фиктивная работа на сетевом графе отображается пунктирной линией .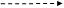

Длина стрелки при построении сетевого графа не связана с временными или стоимостными параметрами и по длине отображается произвольно, в зависимости от желания специалиста или управленца, строящего сетевой граф.

Работы (действительные, ожидания и фиктивные), выходящие из исходного события, не имеют работ непосредственного предшествования, а работы, входящие в завершающее событие, не имеют работ непосредственного следования. Остальные работы могут иметь одну или несколько непосредственно предшествующих и непосредственно следующих работ.

Важным элементом сетевого графа является путь – непрерывная последовательность работ от исходного или от какого-либо промежуточного события до любого конечного (промежуточный путь – фрагмент пути) или до завершающего. Путь определяется по направлению стрелок, причем ни один путь не должен дважды проходить через одно и то же событие. Длина пути рассчитывается как сумма продолжительностей составляющих его работ.

Продолжительность выполнения отдельных работ устанавливается различными методами: расчетно-аналитическим, аналогов, экспертным, различными статистическими методами, например, методом средних оценок и т.д.

Трудоемкость (стоимость) выполнения работ на графе проставляется над стрелкой, которая обозначает данную работу. Различают виды путей: предшествующий событию, полный и критический.

Предшествующий путь – это путь от любого начального события, в том числе исходного, до данного; полный – от исходного до завершающего события; критический – наибольший из продолжительностей полных путей, но наименьший по величине, за время прохождения которого будут выполнены все без исключения работы сетевого графа и наступят все события.

Источник

Сетевой график

Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.

В английском языке для определения сетевого графика используется термин Project Network — is a graph depicting the sequence in which a project’s terminal elements are to be completed by showing terminal elements and their dependencies.

Основной целью использования сетевого графика является эффективное планирование и управление работами и ресурсами проекта. При этом, под ресурсами в данном контексте понимается как оборудование, производственные мощности или денежные средства, так и трудовые ресурсы, внутренние или внешние для организации, выполняющей проект.

Наибольшая эффективность применения сетевого графика достигается при его использовании для планирования проектов или отдельных взаимосвязанных работ. Сетевой график позволяет довольно точно определить плановые сроки завершения проекта и выявить возможные варианты их сокращения. И, что более важно, сетевой график позволяет на ранней стадии планирования проекта выявить критический путь. Кроме этого сетевой график позволяет осуществлять базовый контроль над ходом работ проекта, их сроками и исполнением бюджета.

Виды сетевых графиков

Сетевой график — это граф, на котором события (состояния работ или объектов в определенный момент времени) представлены в виде вершин, а работы проекта представлены в виде дуг, соединяющих вершины графа. Сетевой график, представленный в таком виде, изначально является частью метода PERT (Program Evaluation and Review Technique).

На практике же чаще используется другой вариант сетевого графика, когда вершинами графа являются работы, а дуги обозначают взаимосвязь между ними. Такой вид сетевого графика является частью метода критического пути (англ., CPM — Critical Path Method).

Рассмотрим второй вариант графика и алгоритм его построения подробнее.

Алгоритм построения сетевого графика

Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.

Шаг 1. Определить основную цель проекта

Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.

Шаг 2. Выявить ограничения

Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.

Шаг 3. Определить состав работ

Определить состав работ, необходимых для достижения цели, поставленной на шаге 1.

Шаг 4. Оценить длительность работ

Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.

Шаг 5. Определить последовательность работ

Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.

Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.

Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.

Шаг 6. Указать связи между работами

Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.

Шаг 7. Определить раннее начало и раннее окончание

Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.

Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.

Шаг 8. Определить поздние начало и окончание

Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

Шаг 9. Определить временной резерв

Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

Шаг 10. Выявить критический путь

Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.

Пример построения сетевого графика

Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.

Шаг 1. Определить основную цель проекта

Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.

В этом случае целью нашего небольшого проекта будет — сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.

Шаг 2. Выявить ограничения

Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.

Шаг 3. Определить состав работ

Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:

Отобразим эти работы в виде блоков:

Рисунок 1. Состав работ

Шаг 4. Оценить длительность работ

Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Рисунок 2. Длительность работ

Шаг 5. Определить последовательность работ

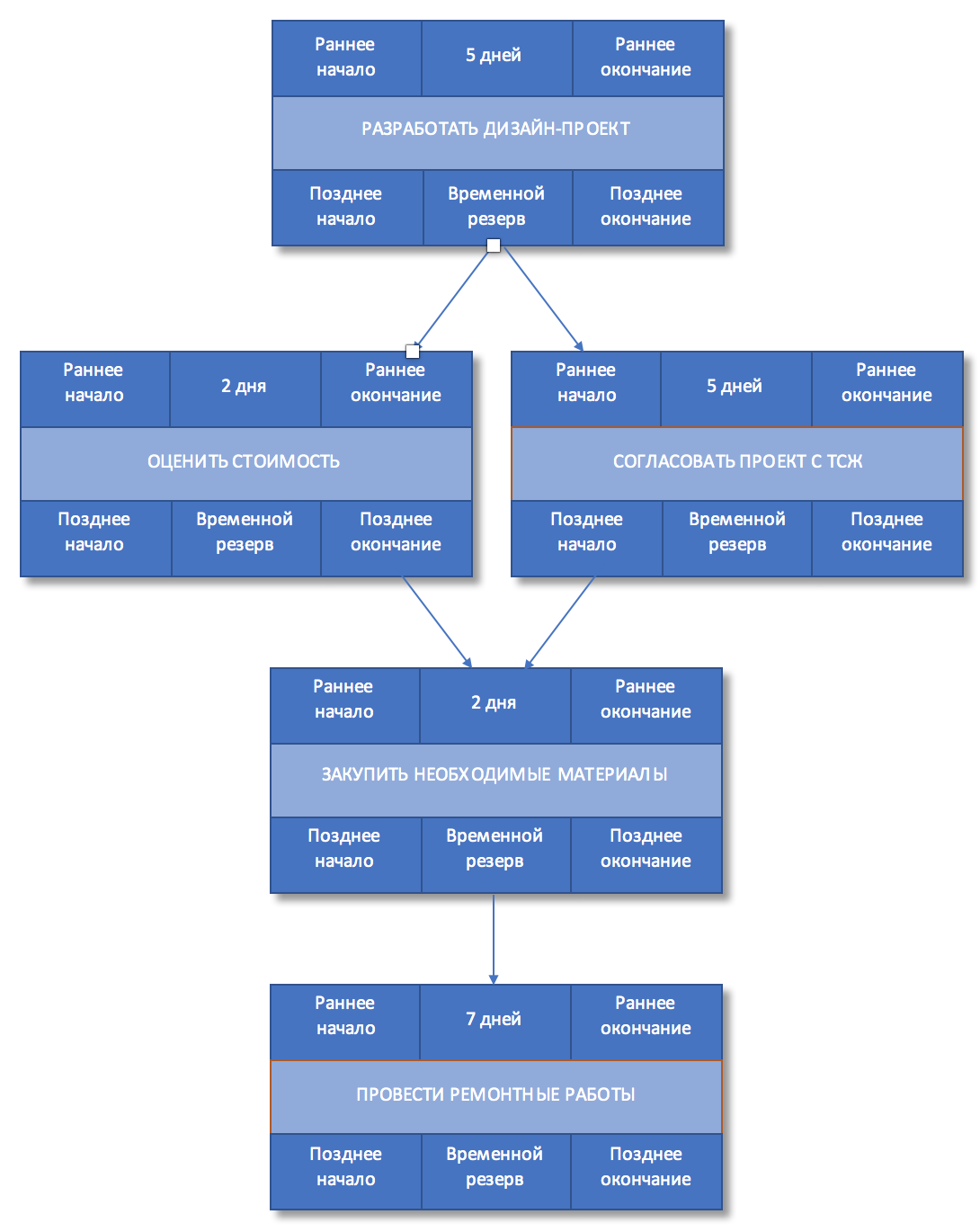
Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Рисунок 3. Последовательность работ

Шаг 6. Указать связи между работами

Укажем стрелками связи между работами.

Рисунок 4. Связи между работами

Шаг 7. Определить раннее начало и раннее окончание

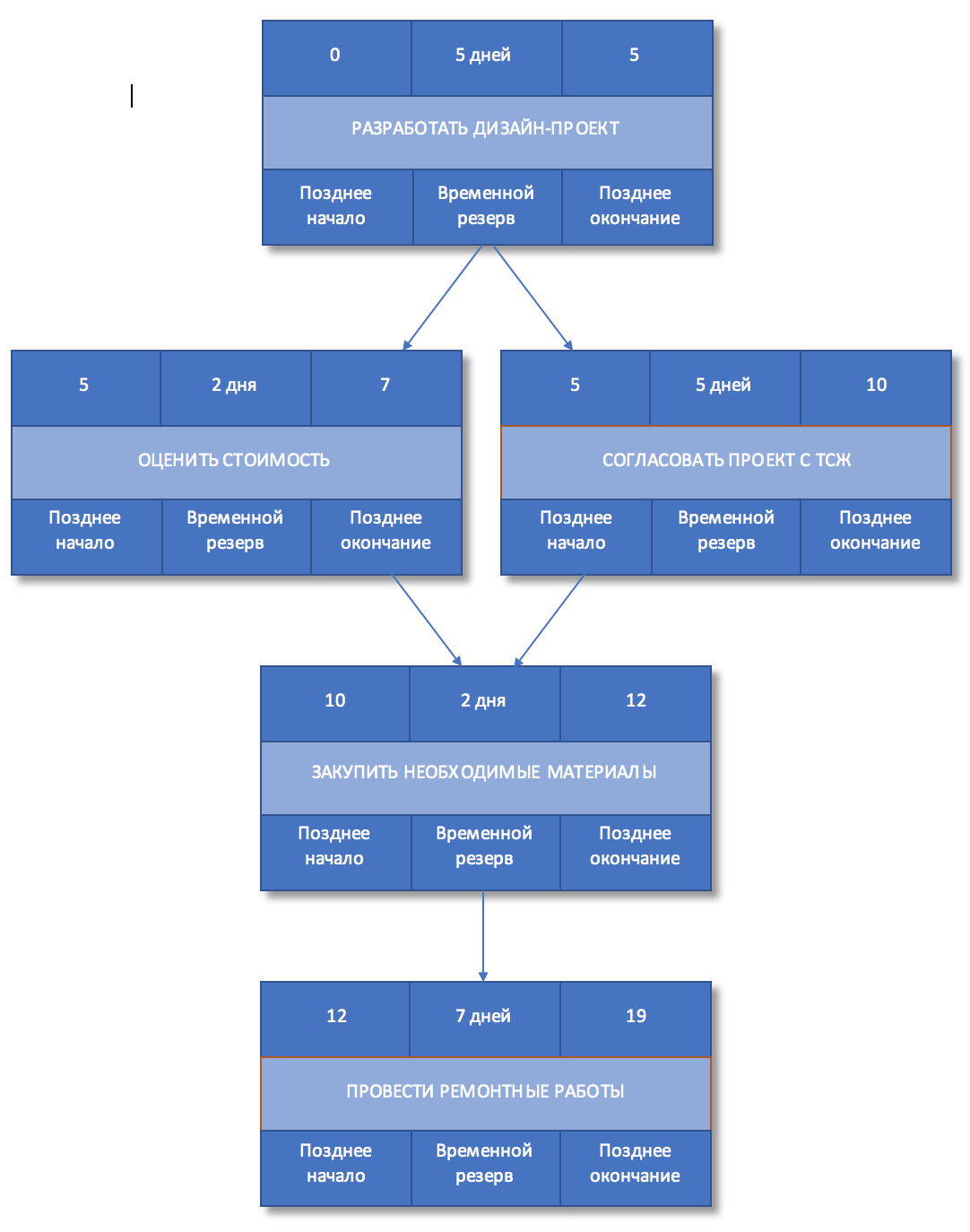
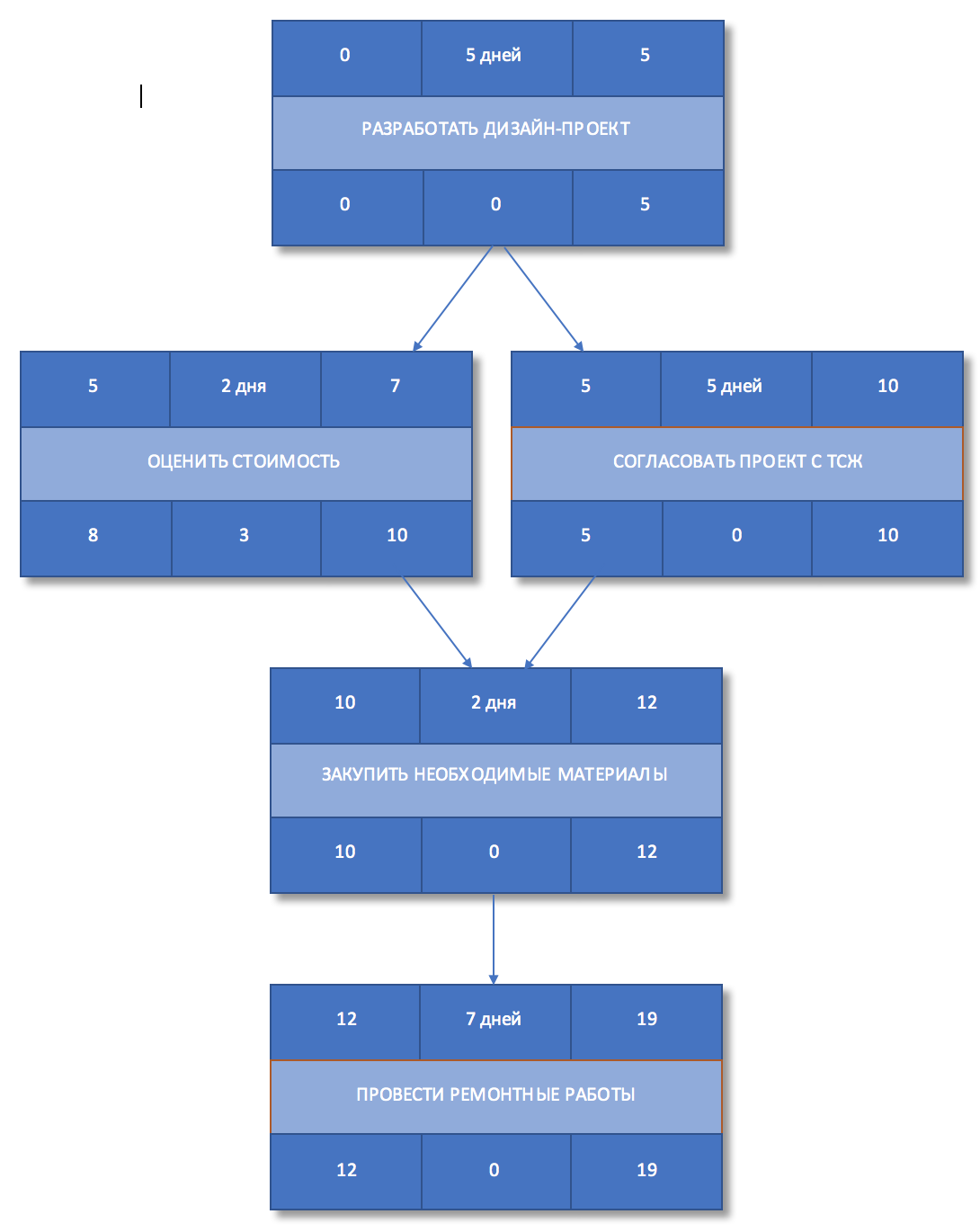
Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.

Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.

Рисунок 5. Раннее начало и окончание работ

Шаг 8. Определить поздние начало и окончание

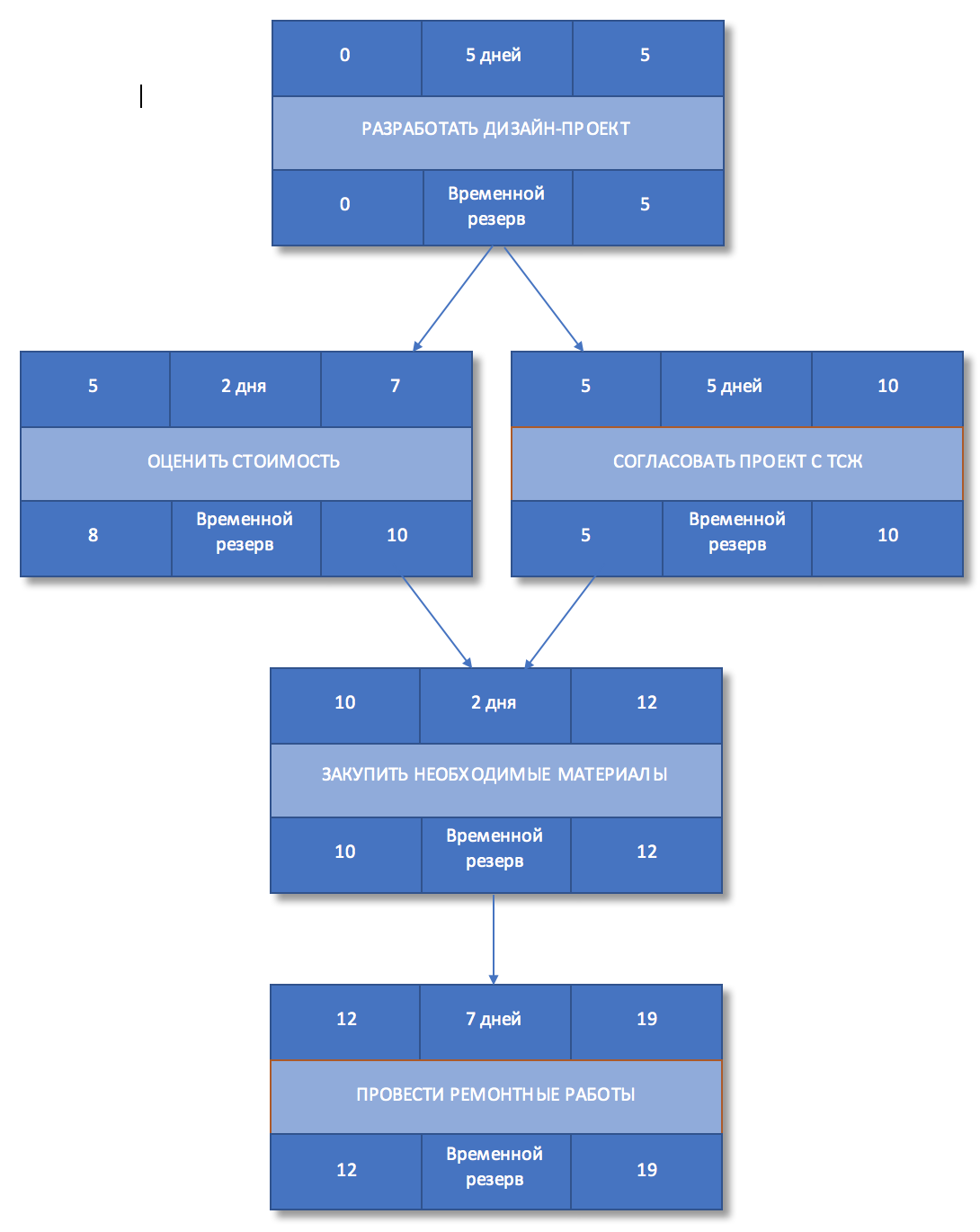
Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

Рисунок 6. Позднее начало и окончание работ

Шаг 9. Определить временной резерв

Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

Рисунок 7. Временной резерв

Шаг 10. Выявить критический путь

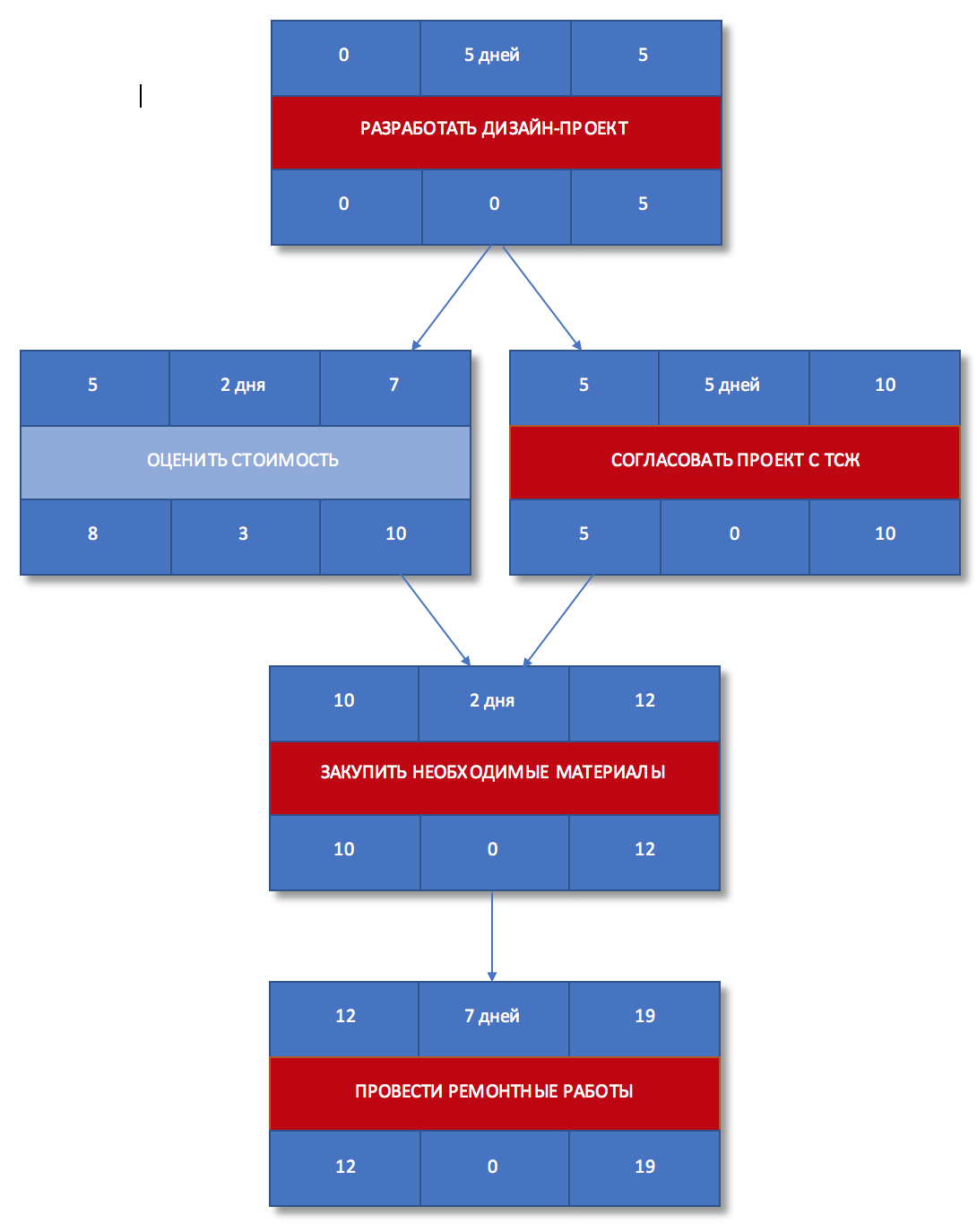
Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.

Рисунок 8. Критический путь

Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.

Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.

We are sorry that this post was not useful for you!

Источник

Что такое сетевой граф

Первым шагом в анализе любого проекта является составление списка входящих в него операций. Детали такого списка зависят от специфики конкретного проекта. Тем не менее во всех случаях необходимо выделить непосредственно предшествующую операцию или операции. Непосредственно предшествующими называются операции, выполнение которых должно быть закончено прежде, чем может начаться данная операция. Например, при постройке дома крыша не может быть построена до того момента, пока не закончится возведение стен.

После того как составлен список, логическая последовательность выполнения операций может быть проиллюстрирована с помощью графа. Существуют различные типы графов, но наиболее широкое применение получили так называемые вершинные и стрелочные графы. Однако каждый из них имеет свои преимущества и недостатки, и выбор того или иного графа является вопросом личных предпочтений или же определяется целью создания и использования данного графа.

10.2.1. Стрелочные графы

В этом типе графов (рис. 10.1) каждая операция представлена стрелкой. Длина стрелок значения не имеет. Направление стрелки отражает ход времени и обычно указывается слева направо. Начало и окончание каждой операции называются событиями и изображаются на графе кружочками или узлом.

Рис. 10.1. Изображение операции на стрелочной графе

Операции обозначают буквой или словом, а события — числом. Поскольку любая операция характеризуется парой событий, ее можно также обозначать с помощью чисел, соответствующих этим событиям. Например, на рис. 10.1 операция А означает то же самое, что и операция (1, 2). Одному узлу может соответствовать (входить или выходить из него) несколько операций. Событие, изображаемое на графе с помощью узла, не считается свершившимся до тех пор, пока не окончены все входящие в него операции. Операция, выходящая из некоторого узла, не может начаться до тех пор, пока не будет достигнуто начальное событие, т.е. пока не будут завершены все операции, входящие в узловое начальное событие.

Если операция С не может быть начата до момента окончания работ А и В, логическую схему данной ситуации можно представить графически следующим образом (см. рис. 10.2).

Начальным событием для С является конечное событие для А и В. Существенно, что в стрелочном графе сохраняется логическая зависимость операций. Иногда, чтобы достичь этого, необходимо включить в граф одну или более фиктивных логических операций.

Рис. 10.2. Логические взаимосвязи в стрелочном графе

Фиктивная логическая стрелка вводится в граф, если необходимо отразить, что некоторое событие не может появиться раньше другого события, а с помощью обычных стрелок, соответствующих операциям, этого сделать нельзя. Функция фиктивной логической операции состоит в том, чтобы показать последовательность появления событий.

Фиктивным логическим операциям ставится в соответствие нулевая продолжительность выполнения, а изображаются они обычно пунктиром. Например, если работу С нельзя начать прежде, чем завершится операция А, а работу D нельзя начать до тех пор, пока не завершатся работы А и В, соответствующий стрелочный граф будет выглядеть следующим образом:

Рис. 10.3. Использование в стрелочном графе фиктивной логической операции

Кроме того, в стрелочных графах для избежания неоднозначности используются фиктивные операции идентификации. В некоторых пакетах прикладных программ, используемых в сетевом анализе, операции обозначаются не с помощью букв или слов, а числами, обозначающими соответствующие им события. Если же Две или более операций выполняются одновременно и имеют одни и те же начальное и конечное события, то компьютер не сможет отличить их друг от друга и не воспримет вводимую исходную информацию. Как показано на рис. 10.4, включение фиктивной операции идентификации позволяет решить данную проблему. На практике принято нумеровать события таким образом, чтобы номер конечного события был больше, чем номер начального события.

Первый шаг после составления списка операций, входящих в проект, состоит в том, чтобы создать таблицу операций, в которой отражаются все операции, а также операции, непосредственно им предшествующие.

Рис. 10.4. Использование в стрелочном графе фиктивной операции идентификации

В данный список не включаются фиктивные логические операции или операции идентификации. На основе полученного списка строится стрелочный сетевой граф, включающий действительные и фиктивные операции и отражающий установленные взаимосвязи между ними. После того, как закончено построение исходного графа, можно выявить и исключить из рассмотрения ненужные фиктивные операции. Затем для улучшения логической схемы исходный граф можно модифицировать и перекомпоновать.

Ненужные фиктивные логические операции можно выявить с помощью простого практического правила. Если единственной операцией, выходящей из некоторого узла, является фиктивная логическая операция, то по всей вероятности без нее можно обойтись.

О Пример 10.1. Компания «Delco pic” — это промышленная фирма, которая заключила контракт о производстве партии станков, предназначеных к использованию крупным предприятием обувной промышленности для массового производства обуви. Ниже перечислены операции, которые необходимо выполнить в процессе разработки и производства этих станков (табл. 10.1):

Таблица 10.1. Таблица операций для задачи из примера 10.1 (см. скан)

Нужно изобразить операции с помощью стрелочного графа.

Сетевой граф должен начинаться с единственного начального события, которое показано на рис. 10.5 кружочком, и заканчиваться единственным конечным событием. Построение графа мы начали с первого события. С этого события начинаются все операции, которым не предшествуют никакие виды работ. Начинать построение полезно с примерного эскиза будущего графа:

Рис. 10.5. Примерный эскиз графа для примера 10.1

В соответствии с приведенной выше таблицей необходимо тщательно, переходя от одной операции к другой, проверить построенный в первом приближении граф. В случае необходимости следует провести его корректировку, а затем для совершенствования схемы построить новый. В данном случае можно исключить все фиктивные логические операции и оставить одну фиктивную операцию идентификации (рис. 10.6).

Рис. 10.6. Новый чертеж стрелочного графа для примера 10.1

Пример 10.2. Компания “Delco pic” является участником другого проекта детали которого приведены ниже:

Таблица 10.2. Таблица операций для примера 10.2 (см. скан)

Изобразим данный проект при помощи стрелочного графа.

Построение начинаем с начального события, обозначенного кружком 1. Из таблицы следует, что существуют три операции — А, В и С, которым не предшествует ни одна из операций. Поэтому из начального события выходят три стрелки. На первый взгляд таблица операций выглядит чрезвычайно простой, однако отразить присущую ей логику с помощью сетевого графа достаточно трудно, вследствие чего мы вынуждены использовать три фиктивные логические операции (см. рис. 10.7).

Рис. 10.7. Стрелочный граф для примера 10.2

Источник