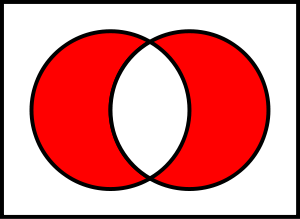
Что такое симметрическая разность
Симметрическая разность
Симметрическая разность двух множеств — это теоретико-множественная операция, результатом которой является множество элементов этих множеств, принадлежащих только одному из них. Симметрическая разность множеств 


Содержание
Определение
Симметрическую разность можно ввести двумя способами:
Понятие симметрической разности можно обобщить на число множеств, большее двух.
Свойства
Пример
См. также
Литература
Полезное
Смотреть что такое «Симметрическая разность» в других словарях:
СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — множеств одна из операций над множествами. Пусть имеются два множества Аи В. Тогда их симметрическая разность обозначается ADB и определяется равенствами где символы означают соответственно операции объединения, пересечения, разности и дополнения … Математическая энциклопедия
СИММЕТРИЧЕСКАЯ РАЗНОСТЬ — порядка пв точке хфункции действительного переменного f(x) выражение Часто также симметрич. разностью называют выражение получающееся из вышеприведенного заменой hна 2h. Если функция f(x).имеет в точке хпроизводную fn (х).порядка п, то Т. П.… … Математическая энциклопедия
Разность множеств — Не следует путать с Симметрическая разность. Разность двух множеств это теоретико множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно… … Википедия
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
Симметричность — может означать: Симметрия Симметричная операция (от нескольких операндов) Симметричная функция (от нескольких переменных) Симметрический многочлен в математической логике: Симметричное отношение в линейной алгебре: Симметричный тензор… … Википедия
Теория множеств — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой… … Википедия
Операции над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
Операция над множествами — Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико множественными операциями или сет операциями. В результате операций из исходных множеств получаются новые … Википедия
ИСЧИСЛЕНИЕ КЛАССОВ — аксиоматич. (см. Аксиоматический метод) описание логики классов. И. к. рав нообъёмно исчислению одноместных предикатов (см. Логика предикатов): у этих исчислений совпадают классы как исходных формул, так и выводимых формул (теорем);… … Философская энциклопедия
Бинарные операции над упорядоченными множествами
В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств.
I. Пересечение упорядоченных множеств
Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.
Сделал небольшую анимацию, чтобы показать как работает алгоритм.
Пример реализации на javascript:
Обращение к функции:
II. Разность упорядоченных множеств
Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
III. Объединение упорядоченных множеств
Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
IV. Симметрическая разность упорядоченных множеств
Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.
По сути это вычитание множеств, сначала A из B, затем B из A.
Симметричная разница
> 
>
Содержание
Свойства [ править ]
А \ треугольник В \ треугольник С> 
> 
>
Симметричная разница также может быть выражена с помощью операции XOR ⊕ над предикатами, описывающими два набора в нотации построителя множеств :
Симметричная разница также может быть выражена как объединение двух множеств за вычетом их пересечения :
Симметричная разность коммутативна и ассоциативна :
Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного множества обе могут быть удалены. Особенно:
Пересечение распределяется по симметричной разнице:
К другим свойствам симметричной разницы относятся:
Эта операция имеет те же свойства, что и симметричная разность множеств.
Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над мультимножеством наборов, дающей набор элементов, которые находятся в нечетном количестве наборов. [ требуется разъяснение ]
Как и выше, симметричная разность набора наборов содержит только элементы, которые находятся в нечетном количестве наборов в коллекции:
| △ M | = ∑ l = 1 n ( − 2 ) l − 1 ∑ 1 ≤ i 1 i 2 … i l ≤ n | M i 1 ∩ M i 2 ∩ … ∩ M i l | <\displaystyle |\triangle M|=\sum _
Симметричная разница в пространствах мер [ править ]
Пока существует понятие «насколько велик» набор, симметричная разница между двумя наборами может считаться мерой того, насколько «далеко друг от друга» они находятся.
является псевдометрикой на Σ. d μ становится метрикой, если Σ рассматривается по модулю отношения эквивалентности X
| μ ( X ) − μ ( Y ) | = | ( μ ( X ∖ Y ) + μ ( X ∩ Y ) ) − ( μ ( X ∩ Y ) + μ ( Y ∖ X ) ) | = | μ ( X ∖ Y ) − μ ( Y ∖ X ) | ≤ | μ ( X ∖ Y ) | + | μ ( Y ∖ X ) | = μ ( X ∖ Y ) + μ ( Y ∖ X ) = μ ( ( X ∖ Y ) ∪ ( Y ∖ X ) ) = μ ( X △ Y ) <\displaystyle <\begin
Расстояние Хаусдорфа против симметричной разности [ править ]
Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками на множестве измеримых геометрических фигур. Однако они ведут себя совершенно иначе. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда хаусдорфово расстояние между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.
См. Также [ править ]
Симметричная разница
> 

>
А \ треугольник В \ треугольник С> 

> 

>
Симметричная разница также может быть выражена с помощью операции XOR ⊕ над предикатами, описывающими два набора в нотации создателя множеств :
Симметричная разница также может быть выражена как объединение двух множеств за вычетом их пересечения :
Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного множества обе могут быть удалены. В частности:
Пересечение распределяется по симметричной разнице:
К другим свойствам симметричной разницы относятся:
Эта операция имеет те же свойства, что и симметричная разность множеств.
Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над мультимножеством наборов, дающей набор элементов, которые находятся в нечетном количестве наборов. [ требуется разъяснение ]
Как и выше, симметричная разность набора наборов содержит только элементы, которые находятся в нечетном количестве наборов в коллекции:
Пока существует понятие «насколько велик» набор, симметричная разница между двумя наборами может считаться мерой того, насколько «далеко друг от друга» они находятся.
является псевдометрикой на Σ. d μ становится метрикой, если Σ рассматривается по модулю отношения эквивалентности X
Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками на множестве измеримых геометрических фигур. Однако они ведут себя совершенно иначе. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда расстояние Хаусдорфа между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.
Python и теория множеств
В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.
Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.
Множество
Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:
Множество – это не более чем неупорядоченная коллекция уникальных элементов.
Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.
Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.
Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.
Множества в Python
Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:
Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:
Для создания пустого множества нужно непосредственно использовать set() :
Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):
Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).
Хешируемые объекты
Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
Объекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два «равных» объекта.
Скорее всего мы предполагаем, что объекты City(«Moscow») должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City :
Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:
Свойства множеств
Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:
Принадлежность множеству
Мощность множества
Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.
Перебор элементов множества
Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.
Отношения между множествами
Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.
Равные множества
Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.
Непересекающиеся множества
Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.
Подмножество и надмножество
Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.
Пустое множество является подмножеством абсолютно любого множества.
Само множество является подмножеством самого себя.
Операции над множествами
Рассмотрим основные операции, опредяляемые над множествами.
Объединение множеств
Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.
Добавление элементов в множество
Пересечение множеств
Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.
Разность множеств
Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.
Удаление элементов из множества
Симметрическая разность множеств
Симметрическая разность множеств – это множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Также симметрическую разность можно рассматривать как разность между объединением и пересечением исходных множеств.
Заключение
Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.