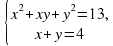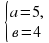Что такое симметрическая система уравнений
Симметрические системы уравнений и системы, содержащие однородные уравнения
Разделы: Математика
Цели урока:
Тип урока: урок изучения нового материала.
Используемые технологии обучения:
Оборудование: компьютер, мультимедийный проектор.
За неделю до урока учащиеся получают темы творческих заданий (по вариантам).
I вариант. Симметрические системы уравнений. Способы решения.
II вариант. Системы, содержащие однородное уравнение. Способы решения.
Каждый ученик, используя дополнительную учебную литературу, должен найти соответствующий учебный материал, подобрать систему уравнений и решить её.
По одному учащемуся от каждого варианта создают мультимедийные презентации по теме творческого задания. Учитель при необходимости проводит консультации для учащихся.
Содержание урока
I. Мотивация учебной деятельности учащихся
Вступительное слово учителя
На предыдущем уроке мы рассматривали решение систем уравнений методом замены неизвестных. Общего правила выбора новых переменных не существует. Однако, можно выделить два вида систем уравнений, когда есть разумный выбор переменных:
II. Изучение нового материала
Учащиеся II варианта отчитываются о проделанной домашней работе.
1. Демонстрация слайдов мультимедийной презентации «Системы, содержащие однородное уравнение» (презентация 1).
Учащиеся записывают в тетради:
2. Работа в парах учащихся, сидящих за одной партой: учащийся II варианта объясняет соседу по парте решение системы, содержащей однородное уравнение.
Отчёт учащихся I варианта.
1. Демонстрация слайдов мультимедийной презентации «Симметрические системы уравнений» (презентация 2).
Учащиеся записывают в тетради:
2. Работа в парах учащихся, сидящих за одной партой: учащийся I варианта объясняет соседу по парте решение симметрической системы уравнений.
III. Закрепление изученного материала
Работа в группах (в группу по 4 ученика объединяются учащиеся, сидящие за соседними партами).
Каждая из 6 групп выполняет следующее задание.
Определить вид системы и решить её:
Учащиеся в группах анализируют системы, определяют их вид, затем, в ходе фронтальной работы обсуждают решения систем.
симметрическая, введем новые переменные x+y=u, xy=v
содержит однородное уравнение.
Пара чисел (0;0) не является решением системы.
IV. Контроль знаний учащихся
Самостоятельная работа по вариантам.
Решите систему уравнений:
Учащиеся сдают тетради учителю на проверку.
V. Домашнее задание
1. Выполняют все учащиеся.
Решите систему уравнений:
2.Выполняют «сильные» учащиеся.
Решите систему уравнений:
VI. Итог урока
Вопросы:
С какими видами систем уравнений вы познакомились на уроке?
Какой способ решения систем уравнений применяется при их решении?
Сообщение оценок, полученных учащимися в ходе урока.
Симметрические системы уравнений
Описание презентации по отдельным слайдам:
Описание слайда:
Симметрические системы уравнений
Автор: Гончаровская Алина
учащаяся 11 класса
МОУ Рощинской СОШ
«Образовательный центр»
Руководитель: Пятовская Людмила Петровна – учитель математики высшей категории
2008-2009 учебный год
Описание слайда:
1. Введение
2. Понятие симметрии, её основные виды
3. Решение задач при помощи симметрии
4. Симметрические системы
5. Способы решения симметрических систем. Метод замены переменных
6. Теоремы, используемые при решении симметрических систем
7. Заключение
8. Список используемой литературы
Описание слайда:
Введение
Проблема моего проекта заключается в том, что для успешной сдачи ЕГЭ требуется умение решать различные системы уравнений, а в курсе средней школы им отведено недостаточно времени, необходимого познать этот вопрос глубже.
Цель работы: подготовиться к успешной сдачи ЕГЭ.
Задачи работы:
Расширить свои знания в области математики, связанные с понятием «симметрия».
Повысить свою математическую культуру, используя понятие «симметрия» при решении систем уравнений, называемых симметрическими, а также других задач математики.
Описание слайда:
Понятие симметрии.
Симме́три́я — (др.-греч. συμμετρία), в широком смысле — неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы. Двусторонняя симметрия означает, что право и лево относительно какой-либо плоскости выглядят одинаково.
Описание слайда:
Симметрия бывает:
двусторонняя;
симметрия n-порядка;
аксиальная;
сферическая;
трансляционная
Описание слайда:
Описание слайда:
Задача №2
На плоскости дана прямая l и точки A и B по одну сторону от неё. Нужно найти на прямой такую точку C, чтобы сумма длин отрезков AC и BC была минимальна.
Решение. Построим точку A’, симметричную A относительно прямой l. Заметим, что для любой точки C, лежащей на прямой l, AC=A’C. Поэтому
AC+BC=A’C+BC.
В силу неравенства треугольника сумма A’C+BC минимальна тогда и только тогда, когда точка C лежит на отрезке A’B (рис. 2). Итак, C=A’B l.
Описание слайда:
Описание слайда:
Описание слайда:
Последняя задача и является примером симметрической системы.
Функция f (x;y) называется симметрической, если для всех x и y выполнено равенство
Например: Многочлен от двух переменных вида f(x,y) = 3x 2 – 2xy + 3y 2+ 15является симметрической функцией. В самом деле,
Описание слайда:
Описание слайда:
Описание слайда:
Пример №1:
х 2+ ху + у 2 =13,
х + у = 4;
Пусть х + у = u, ху = v.
v = 3,
u = 4;
Произведем обратную замену.
х = 4 – у,
у 1 = 3; у 2= 1;
х 1 = 1, х 2 = 3,
у 1 = 3, у 2 = 1.
Описание слайда:
Пример №2
3 х 2у – 2ху + 3ху 2 = 78,
2х – 3ху + 2у + 8 = 0
Описание слайда:
Решим теперь следующую совокупность систем
Описание слайда:
Пример №3:
Решение:
Возведем второе уравнение в куб, получим:
Таким образом, по теореме Виета,
и
являются корнями квадратного
уравнения
Отсюда
и
Значит,
Заметим, что мы нашли один из корней уравнения
Ответ:
Описание слайда:
Теоремы, используемые при решении симметрических систем.
Теорема 1. (о симметрических многочленах)
Любой симметрический многочлен от двух переменных представим в виде функции от двух основных симметрических многочленов
Другими словами, для любого симметрического многочлена f (x, y) существует такая функция двух переменных φ (u, v), что
Описание слайда:
Теорема 2. (о симметрических многочленах)
Любой симметрический многочлен от трёх переменных представим в виде функции от трёх основных симметрических многочленов:
Другими словами, для любого симметрического многочлена f (x, y) существует такая функция трёх переменных θ (u, v, w), что
Описание слайда:
Описание слайда:
Описание слайда:
Если х ≥ 1, то:
а) х > у и у у и у ≥ 1 система принимает вид
х – у + у 2 = 3,
х – 1 + у – 1 = 2,
или
х – у + у 2 = 3,
х + у = 4,
откуда находим х = 1, у = 3. Эта пара чисел не принадлежит рассматриваемой области;
Описание слайда:
Описание слайда:
Заключение
Математика развивает мышление человека, учит посредством логики находить разные пути решения. Так, научившись решать симметрические системы, я поняла, что использовать их можно не только для выполнения конкретных примеров, но я для решения разного рода задач.
Я думаю, что проект может принести пользу не только мне. Для тех, кто так же захочет ознакомиться с этой темой, моя работа будет являться хорошим помощником.
Описание слайда:
Список используемой литературы:
Башмаков М. И., «Алгебра и начала анализа», 2-е издание, Москва, «Просвещение», 1992, 350 стр.
Рудченко П. А., Яремчук Ф. П., «Алгебра и элементарные функции», справочник; издание третье, переработанное и дополненное; Киев, Наукова, Думка, 1987, 648 стр.
Шарыгин И. Ф., « Математика для школьников старших классов», Москва, издательский дом «Дрофа», 1995, 490 стр.
Интернет-ресурсы: http://www.college.ru/
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Факультативное занятие по матемтаике «Системы симметрических уравнений»
Описание разработки
Учащиеся, привыкшие решать системы привычными тремя способами, сталкиваются с проблемой: Как решить системы, если нельзя выполнить почленного сложения, красиво выразить одну переменную через другую. В этом случае может помочь универсальная подстановка рассмотренная в данной разработке. Разабрав примеры с учителем, в групповой работе учащиеся смогут использовать данную подстановку при решении систем уравнений третий степени.
Система уравнений называется симметрической (симметричной), если при замене переменной х на переменную у и у на переменную х, уравнения, входящие в систему, не изменятся.
В любой симметричной системе уравнений ответы симметричны, т.е. если пара чисел (х0, у0) – решение системы, то пара чисел (у0, х0) тоже является решением.
Симметричные системы можно решать методом замены переменных, в роли которых выступают основные симметрические многочлены. Симметрическая система двух уравнений с двумя неизвестными х и у решается подстановкой u = x+y, v = xy
х 2 + у 2 = (х + у) 2 – 2ху = u 2 – 2v
x 3 + y 3 = (x + y)(x 2 – xy + y 2 ) = u(u 2 – 2v – v) = u 3 – 3uv и тд
Взаимопроверка и разбор спорных заданий.
Содержимое разработки
Факультатив по математике
Разработка занятия по теме:
Системы симметрических(симметричных) уравнений
Система уравнений называется симметрической (симметричной), если при замене переменной х на переменную у и у на переменную х, уравнения, входящие в систему, не изменятся.
В любой симметричной системе уравнений ответы симметричны, т.е. если пара чисел (х0, у0) – решение системы, то пара чисел (у0, х0) тоже является решением.
Симметричные системы можно решать методом замены переменных, в роли которых выступают основные симметрические многочлены. Симметрическая система двух уравнений с двумя неизвестными х и у решается подстановкой u = x+y, v = xy
х 2 + у 2 = (х + у) 2 – 2ху = u 2 – 2v
x 3 + y 3 = (x + y)(x 2 – xy + y 2 ) = u(u 2 – 2v – v) = u 3 – 3uv и тд
Решите систему уравнений:
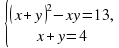
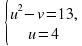
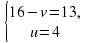
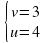
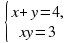
Решите систему уравнений:
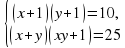
Замена х + у = а, ху = в
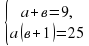
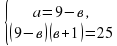
Произведем обратную замену.
Решите системы уравнений:
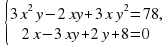
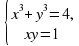
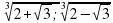
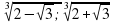
Взаимопроверка и разбор спорных заданий.
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №14. Алгебраические системы уравнений.
Перечень вопросов, рассматриваемых в теме:
1) определение алгебраической системы уравнений;
2) методы решений алгебраических систем уравнений;
3) симметрические системы уравнений.
Системами уравнений называют записи, представляющие собой расположенные друг под другом уравнения, объединенные слева фигурной скобкой, которые обозначают множество всех решений уравнений, одновременно являющихся решениями каждого уравнения систем.
Решением системы уравнений с двумя переменными называется пара значений этих переменных, обращающая каждое уравнение системы в верное числовое равенство, другими словами, являющаяся решением каждого уравнения системы.
Систему уравнений 
Уравнение P(x;y)= а, где
Систему двух уравнений с двумя переменными называют симметрической системой, если оба ее уравнения — симметрические.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
К определению системы уравнений будем подбираться постепенно. Сначала лишь скажем, что его удобно дать, указав два момента: во-первых, вид записи, и, во-вторых, вложенный в эту запись смысл. Остановимся на них по очереди, а затем обобщим рассуждения в определение систем уравнений.
Пусть перед нами несколько каких-нибудь уравнений. Для примера возьмем два уравнения 2·x+y=−3 и x=5. Запишем их одно под другим и объединим слева фигурной скобкой:
Записи подобного вида, представляющие собой несколько расположенных в столбик уравнений и объединенных слева фигурной скобкой, являются записями систем уравнений.
Что же означают такие записи? Они задают множество всех таких решений уравнений системы, которые являются решением каждого уравнения.
Не помешает описать это другими словами. Допустим, какие-то решения первого уравнения являются решениями и всех остальных уравнений системы. Так вот запись системы как раз их и обозначает.
А теперь можно сформулировать определение.
Определение. Системами уравнений называют записи, представляющие собой расположенные друг под другом уравнения, объединенные слева фигурной скобкой, которые обозначают множество всех решений уравнений, одновременно являющихся решениями каждого уравнения систем.
Мы будем решать сегодня, в основном, системы уравнений с двумя переменными.
Определение. Решением системы уравнений с двумя переменными называется пара значений этих переменных, обращающая каждое уравнение системы в верное числовое равенство, другими словами, являющаяся решением каждого уравнения системы.
Рассмотрим методы решения систем уравнений.
Методы решения систем уравнений.
Алгоритм решения системы двух уравнений с двумя переменными x,y методом подстановки:
1. Выразить одну переменную через другую из одного уравнения системы (более простого).
2. Подставить полученное выражение вместо этой переменной в другое уравнение системы.
3. Решить полученное уравнение и найти одну из переменных.
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения в уравнение, полученное на первом шаге и найти вторую переменную.
5. Записать ответ в виде пар значений, например, (x;y), которые были найдены соответственно на третьем и четвёртом шаге.
Решить систему уравнений
1. Выразим x через y из второго (более простого) уравнения системы x=5+y.
2. Подставим полученное выражение вместо x в первое уравнение системы (5+y)⋅y=6
3. Решим полученное уравнение:
4. Подставим поочерёдно каждое из найденных значений y в уравнение x=5+y, тогда получим:
5. Пары чисел (−1;−6) и (6;1) — решения системы.
Алгоритм решения системы двух уравнений с двумя переменными x,y методом сложения:
1. Уравнять модули коэффициентов при одном из неизвестных.
2. Сложить или вычесть уравнения.
3. Решить полученное уравнение с одной переменной.
4. Подставить поочерёдно каждый из найденных на третьем шаге корней уравнения в одно из уравнений исходной системы, найти второе неизвестное.
5. Записать ответ в виде пар значений, например, (x;y), которые были найдены.
При решении систем двух уравнений с двумя переменными метод введения новых переменных можно применять двумя способами:
1. вводится одна новая переменная и используется только в одном уравнении системы;
2. вводятся две новые переменные и используются одновременно в обоих уравнениях системы.
Решение: введем новые переменные xy= u, x+y=v.
Тогда систему можно переписать в более простом виде:
Решением системы является две пары чисел.
Однако пара (0;0), являющаяся решением первого уравнения системы, не удовлетворяет второму уравнению, т. к. 0²-3·0·0 + 0² = 0 ≠-1. Отсюда х ≠0, и поэтому можем обе части первого уравнения системы разделить на х² ≠ 0 (это не приведет к потере корней). Разделив обе части первого уравнения системы на х², получим

Таким образом, исходная система равносильна совокупности двух систем уравнений:
Решить систему уравнений
Сложим уравнения почленно.
Решим полученное уравнение с одной переменной.
Подставим поочередно каждый из найденных корней уравнения
в одно из уравнений исходной системы, например во второе, и найдём второе неизвестное.
если х=5, то 25+y 2 =29
если х=-5, то 25+y 2 =29
Пары чисел (−5;−2), (−5;2), (5;−2) и (5;2) — решения системы.