Что такое симметричная ось
Осевая симметрия — виды, свойства и примеры фигур
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
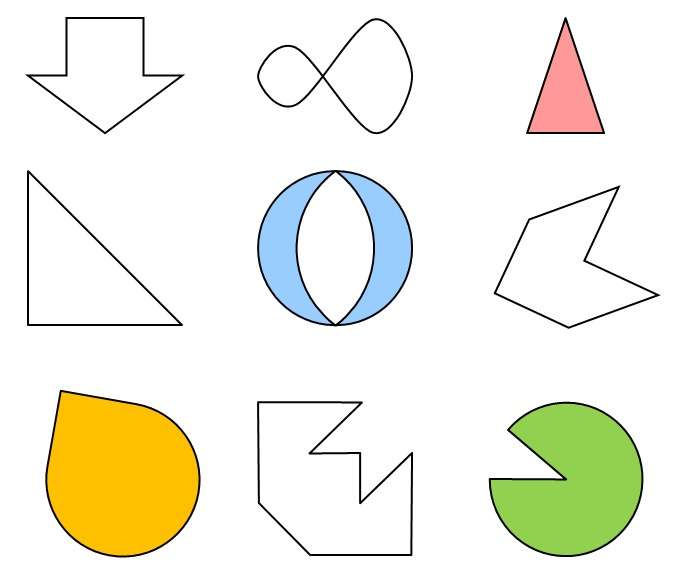
Рис. 1 Фигуры, обладающие симметричностью
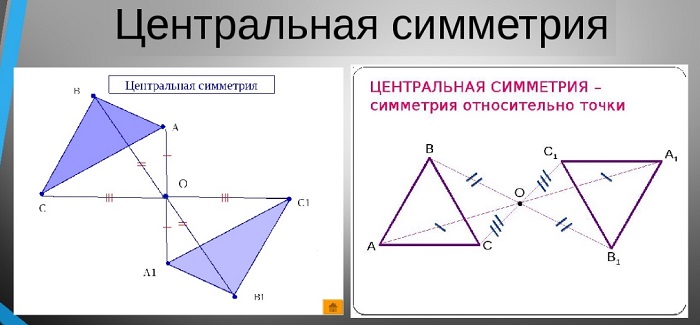
Центральная симметрия
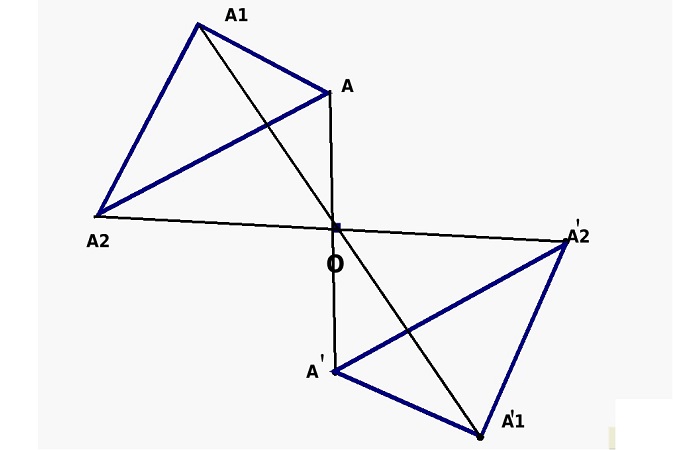
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.
Рис. 2 Графическое представление центральной симметрии
Осевая симметрия
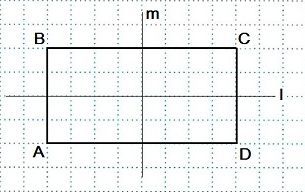
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.
Рис. 3 Наглядное представление осевой симметрии
Объект симметричен относительно прямой, если все его точки имеют такие же симметричные аналоги относительно этой прямой. Она же — центр симметрии.
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.
Рис. 4 Примеры осевой симметрии
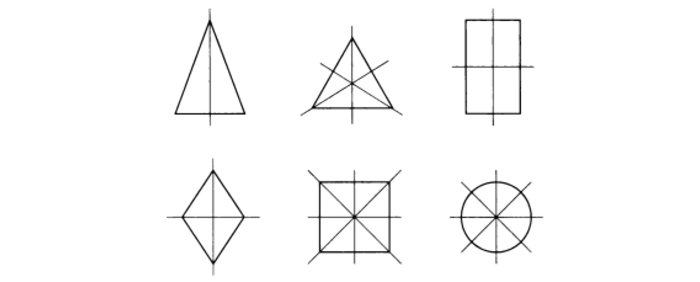
Фигуры, имеющие несколько осей симметрии
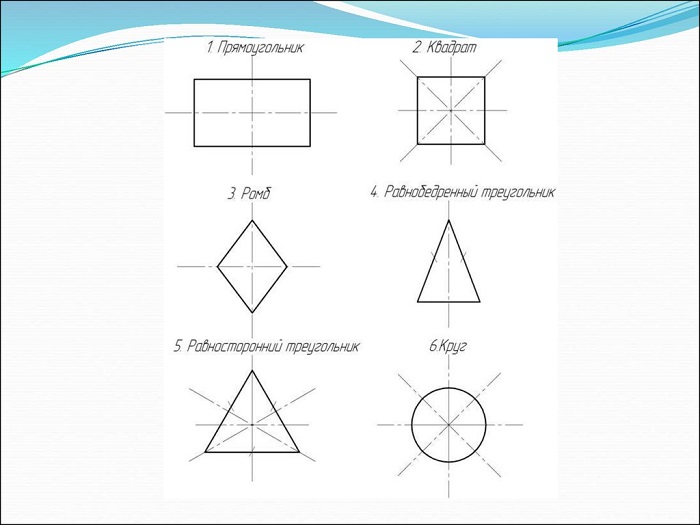
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
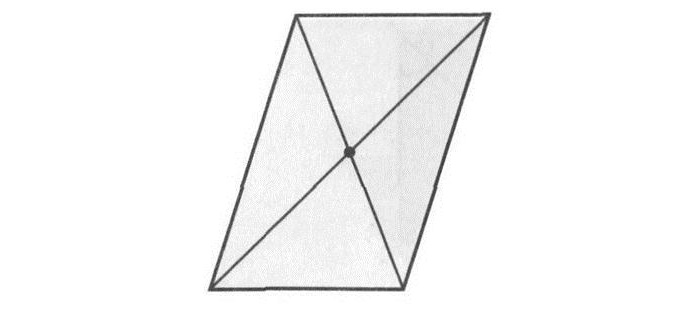
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
Рис. 5 Оси симметрии ромба
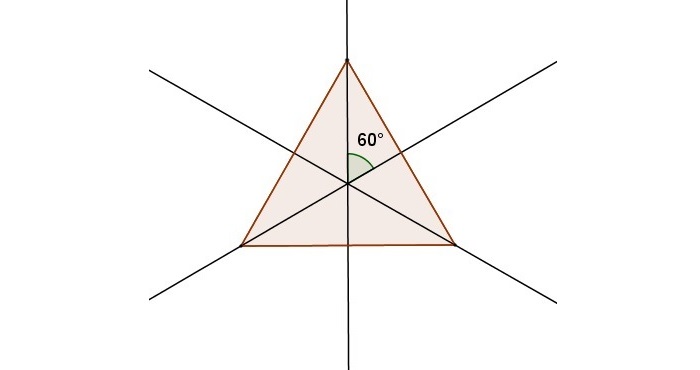
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Симметрия

Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.
Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.
Вывод
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
Рис. 1 Фигуры, обладающие симметричностью
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.
Рис. 2 Графическое представление центральной симметрии
Осевая симметрия
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.
Рис. 3 Наглядное представление осевой симметрии
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.
Рис. 4 Примеры осевой симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
Рис. 5 Оси симметрии ромба
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Ось симметрии
Осевая симметрия — тип симметрии, имеющий два несколько отличающихся определения:
Применительно к плоскости эти оба вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).
Иногда вводят также (осевую) симметрию некоторого порядка:
Смотреть что такое «Ось симметрии» в других словарях:
ОСЬ СИММЕТРИИ — в кристаллографии прямая линия, при повороте вокруг которой на определенный угол симметричная фигура займет в пространстве то же положение, которое она занимала до поворота, но на место одних ее частей переместятся др. такие же части. Наименьший… … Геологическая энциклопедия
ось симметрии — Прямая, при повороте вокруг которой на некоторый угол кристалл или узлы кристаллической решетки совмещаются сами с собой. [http://metaltrade.ru/abc/a.htm] Тематики металлургия в целом EN axis of symmetry … Справочник технического переводчика
ось симметрии — 3.33 ось симметрии: Воображаемая линия, проходящая через бриллиант, на равном расстоянии от которой в противоположных направлениях находятся одинаковые элементы огранки бриллианта. Источник: ГОСТ Р 52913 2008: Бриллианты. Классификация.… … Словарь-справочник терминов нормативно-технической документации
ось симметрии — simetrijos ašis statusas T sritis Standartizacija ir metrologija apibrėžtis Ašis, apie kurią sukamos figūros simetrijos taškai sutampa. atitikmenys: angl. symmetry axis vok. Symmetrieachse, f rus. ось симметрии, f pranc. axe de répétition, m; axe … Penkiakalbis aiškinamasis metrologijos terminų žodynas
ось симметрии — simetrijos ašis statusas T sritis chemija apibrėžtis Ašis, apie kurią sukamos figūros simetrijos taškai sutampa. atitikmenys: angl. symmetry axis rus. ось симметрии ryšiai: sinonimas – inversijos ašis … Chemijos terminų aiškinamasis žodynas
ось симметрии — simetrijos ašis statusas T sritis fizika atitikmenys: angl. axis of symmetry; symmetry axis vok. Symmetrieachse, f rus. ось симметрии, f pranc. axe de symétrie, m … Fizikos terminų žodynas
ось симметрии — [axis of symmetry] прямая, при повороте вокруг которой на некоторый ∠α кристалл или узлы кристаллической решетки совмещаются сами с собой; Смотри также: Ось ось текстуры ось легкого намагничивания гидростатическая ось … Энциклопедический словарь по металлургии
ОСЬ СИММЕТРИИ ЗЕРКАЛЬНО-ПОВОРОТНАЯ — элемент симметрии, применяемый некоторыми кристаллографами вместо инверсионных осей; это совокуп. оси и перпендикулярной к ней плоскости симметрии, действующих совместно. Все возможные в к лах О. с. з. п. (обозн. через Л) соответствуют известным… … Геологическая энциклопедия
ОСЬ СИММЕТРИИ ГЛАВНАЯ — ось симметрии высшего порядка (L3, L4, L6) в средних сингониях. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
ОСЬ СИММЕТРИИ ПОЛЯРНАЯ — ось симметрии с разными концами, соединяющая разл. элементы огранения кристалла. Свойства по противоположным направлениям таких осей различны. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
Осевая симметрия: свойства, примеры и упражнения
Содержание:
В осевая симметрия Это происходит, когда точки одной фигуры совпадают с точками другой фигуры посредством прямой биссектрисы, называемой осью симметрии. Это также называется радиальной, вращательной или цилиндрической симметрией.
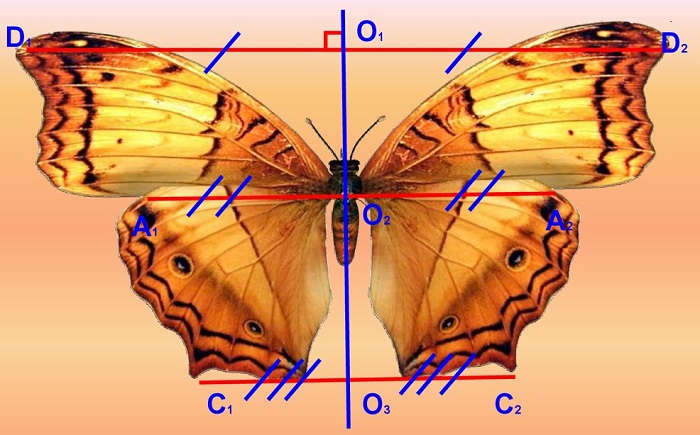
Обычно он применяется в геометрических фигурах, но его легко наблюдать в природе, поскольку есть такие животные, как бабочки, скорпионы, божьи коровки или люди, которые демонстрируют осевую симметрию.
Как найти осесимметричный
Чтобы найти осесимметричную P ‘точки P относительно прямой (L), выполняются следующие геометрические операции:
1.- Перпендикуляр к линии (L), проходящей через точку P.
2.- Перехват двух линий определяет точку O.
3.- Измеряется длина сегмента PO, затем эта длина копируется на линию (PO), начиная с точки O в направлении от P к O, определяя точку P ‘.
4. Точка P ‘является осевой симметрией точки P относительно оси (L), так как линия (L) является срединной точкой сегмента PP’, будучи O средней точкой указанного сегмента.
Свойства осевой симметрии
— Осевая симметрия изометрична, то есть расстояния геометрической фигуры и соответствующая ей симметрия сохраняются.
— Мера угла и его симметричности равны.
— Симметричная линия линии, параллельной оси симметрии, также является линией, параллельной указанной оси.
— Секущая к оси симметрии имеет в качестве симметричной другой секущую линию, которая, в свою очередь, пересекает ось симметрии в той же точке на исходной прямой.
— Прямая и ее осевая симметричная линия образуют угол, биссектриса которого является осью симметрии.
Примеры осевой симметрии
Природа демонстрирует множество примеров осевой симметрии. Например, вы можете увидеть симметрию лиц, насекомых, таких как бабочки, отражение на спокойных водных поверхностях и зеркалах или листьях растений и многое другое.
Упражнения осевой симметрии
Упражнение 1
У нас есть треугольник вершин A, B и C, декартовы координаты которого соответственно равны A = (2, 5), B = (1, 1) и C = (3,3). Найдите декартовы координаты треугольника, симметричного относительно оси Y (оси ординат).
Решение: Если точка P имеет координаты (x, y), то ее симметричность относительно оси ординат (оси Y) равна P ’= (- x, y). Другими словами, значение его абсциссы меняет знак, а значение ординаты остается прежним.
В этом случае симметричный треугольник с вершинами A ‘, B’ и C ‘будет иметь координаты:
A ‘= (- 2, 5); B ‘= (- 1, 1) и C’ = (- 3, 3), как показано на рисунке 6.
Упражнение 2.
Что касается треугольника ABC и его симметричного A’B’C ‘из упражнения 1, убедитесь, что соответствующие стороны исходного треугольника и его симметричной стороны имеют одинаковую длину.
Решение: Чтобы найти расстояние или длину сторон, мы используем формулу Евклидова расстояния:
Длина соответствующей симметричной стороны A’B ‘рассчитывается ниже:
d (A ‘, B’) = √ ((Bx’-Ax ‘) ^ 2 + (By’-Ay’) ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
Таким образом проверяется, что осевая симметрия сохраняет расстояние между двумя точками. Процедуру можно повторить для двух других сторон треугольника и его симметрии, чтобы проверить неизменность длины. Например | AC | = | A’C ’| = √5 = 2,236.
Упражнение 3.
Что касается треугольника ABC и его симметричного A’B’C ‘из упражнения 1, убедитесь, что соответствующие углы исходного треугольника и его симметричного треугольника имеют одинаковую угловую меру.
Решение: Чтобы определить меры углов BAC и B’A’C ’, сначала будет вычислено скалярное произведение векторов. AB с участием AC а затем скалярное произведение A’B ’ с участием A’C ’.
A = (2, 5), B = (1, 1) и C = (3,3)
A ‘= (- 2, 5); B ‘= (- 1, 1) и C’ = (- 3, 3).
AB = и AC =
A’B ’ = и AC =
Затем находятся следующие скалярные произведения:
Измерение угла ВАС составляет:
∡BAC = ArcCos ( AB⋅AC / (|AB |⋅|AC |)) =
ArcCos (7 / (4,123⋅2,236)) = 40,6º
Точно так же величина угла B’A’C ’равна:
∡B’A’C ’= ArcCos ( A’B’⋅A’C ’ / (|A’B ’|⋅|A’C ’|)) =
ArcCos (7 / (4,123⋅2,236)) = 40,6º
Таким образом, осевая симметрия сохраняет меру углов.
Упражнение 4.
Пусть точка P имеет координаты (a, b). Найдите координаты его осевой симметрии P ‘относительно прямой y = x.
Решение: Будем называть (a ’, b’) координатами симметричной точки P ’относительно прямой y = x. Средняя точка M отрезка PP ’имеет координаты ((a + a’) / 2, (b + b ’) / 2) и также находится на прямой y = x, поэтому выполняется следующее равенство:
Решая два предыдущих равенства a ‘и b’, делаем вывод, что:
То есть для данной точки P (a, b) ее осевая симметрия относительно линии y = x равна P ’(b, a).
Ссылки
Право Пернада: происхождение, миф или реальность?