Что такое симметрия в рисунке
Как нарисовать симметричный предмет
Сегодня мы с вами поговорим о явлении, с которым каждому из нас приходится постоянно встречаемся в жизни: о симметрии. Что такое симметрия?
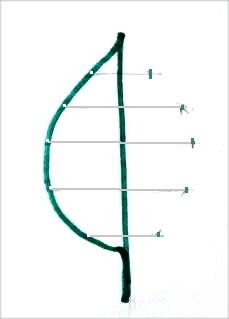
Но перейдем к практике. Начинать со сложных объектов вроде людей и животных не стоит, попробуем в качестве первого упражнения на новом поприще дорисовать зеркальную половинку листа.
Следим, чтобы получилось как можно более похоже. Для этого будем буквально строить нашу половинку. Не подумайте, что так легко, тем более с первого раза, одним росчерком провести зеркально-соответствующую линию!
Полученные точки соединим карандашной линией:
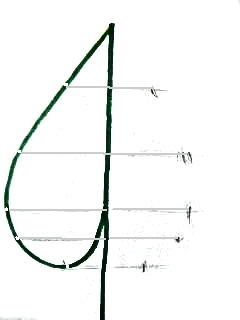
Лист тополя дорисовали, теперь можно замахнуться и на дубовый.
Вот и симметричный лист дуба нарисовался, вернее, мы его построили по всем правилам:
Поглядите на получившуюся работу издали и оцените насколько точно нам удалось передать требуемое сходство. Вот вам совет: поглядите на ваше изображение в зеркале, и оно вам укажет, есть ли ошибки. Другой способ: перегните изображение точно по оси (правильно перегибать мы с вами уже научились) и вырежьте листик по изначальной линии. Посмотрите на саму фигуру и на отрезанную бумагу.
Ладно, знать будем и впредь буду проверять свои построения тщательнее.
Осевая и центральная симметрия
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
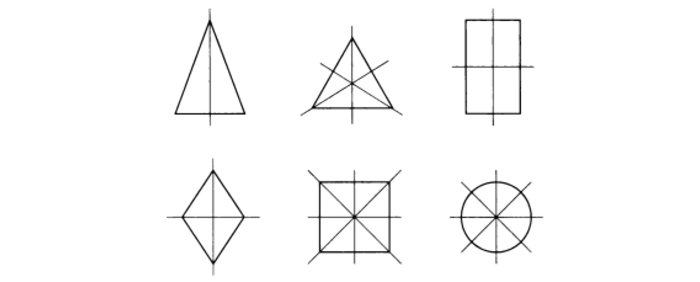
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
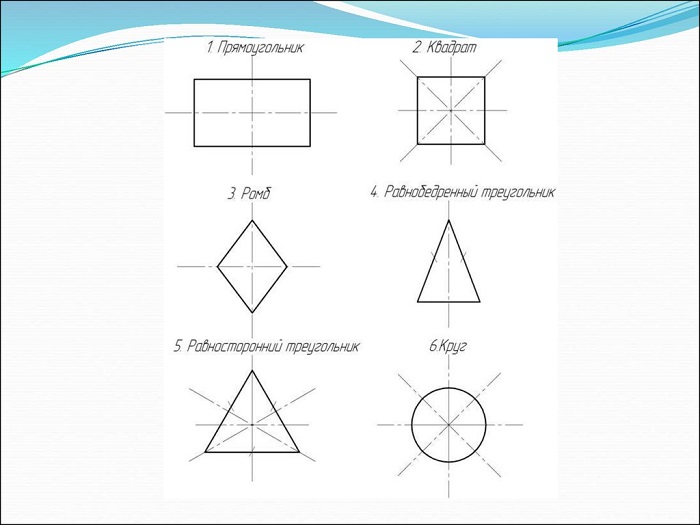
Рассмотрите фигуры с осевой и центральной симметрией.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
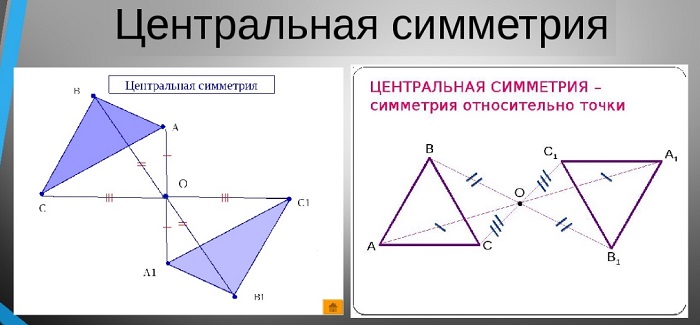
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
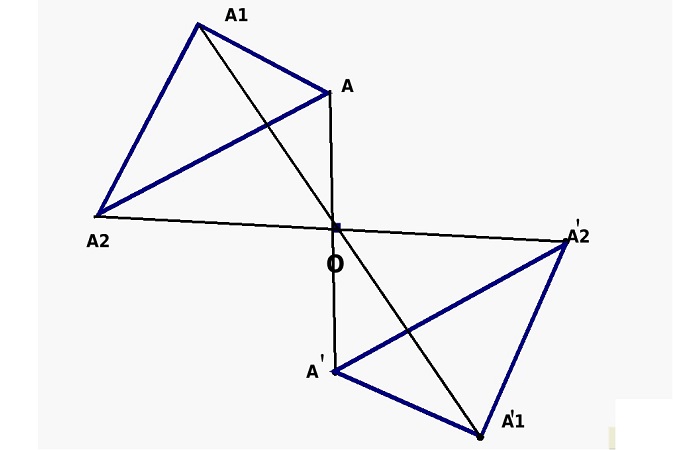
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Симметрия в композиции: примеры с фотографиями
Привет! Сегодня разговор пойдет об одном из самых больших удовольствий перфекционистов. А если точнее – симметрия в композиции.
Для начала
При взгляде на фотографию, где одна часть отражает другую, некоторые люди испытывают, прямо-таки, физическое наслаждение. А вот другая категория не чувствует ничего, тем не менее, это только на первый взгляд.
Дело в том, что, когда мы смотрим на симметричное изображение, наш мозг фиксирует определенный интервал между объектами и релаксирует. А когда этот интервал от объекта к объекту разнится, извилины начинают нервничать.
Одинаковая со всех сторон
Поэтому, начнем с самых популярных видов симметрии – зеркальной и осевой. Если простыми словами, то зеркальная – это когда одна часть композиции строго отражает противоположную относительно горизонтальной плоскости. А осевая – отражение относительно вертикальной оси. Пример осевой на фотографии ниже.
Интересно, что Леонардо да Винчи писал левой рукой справа налево. Если бы мы могли приложить зеркало к его записям, то увидели бы прекрасный пример зеркальной симметрии.
Полной идентичности двух частей одного целого в природе, конечно же, не бывает. А в творениях человека можно увидеть зеркальное отражение одной части к другой. Архитектура — прекрасное тому доказательство.
Центр точки
Еще один вид – центральная. Отличным образцом такого эффекта является окружность. Эта фигура, которая одинакова со всех сторон относительно своей центральной точки.
В мире существует огромное многообразие форм, которые это показывают. Фрукты, цветы, животные. И снова без творений руки человеческой не обошлось – колесо обозрения, например. Но, пожалуй, самым сочный примером центральной симметрии является апельсин.
Золотое сечение
Ни для никого не секрет, что винтовая ритмичность завораживает человечество на протяжении многих лет. Люди уверены, что спираль хранит в себе огромное количество загадок, а для некоторых – сакральный смысл. Даже наша ДНК похожа на винтовую лестницу.
На фотографиях и рисунках винтовая гармония выглядит чарующе. Бесконечные витки притягивают взгляд и заставляют задуматься с чего же все «закрутилось»?
Так называемая «Последовательность Фибоначчи» или «Золотое сечение» встречается повсеместно – шишка, подсолнух, суккуленты, раковина Наутилуса, и т.д.
Раковина, кстати, одна из самых очаровательных геометрических фигур. Даже на картине Леонардо да Винчи можно проследить проекцию Золотого сечения.

В искусстве фотографии и живописи очень часто применяется «Правило Золотого сечения». И правильно! Не нужно изобретать велосипед, природа все продумала задолго до нас.
Ведь элементы изображения должны сочетаться друг с другом. Чтобы кадр получился гармоничным, главный объект необходимо «поместить» в центр спирали.
Снежинка под углом
Вы помните форму снежинки? А морской звезды? А если они повернутся под углом 90 градусов? Или 180? Ничего не изменится, потому что после поворота они останутся абсолютно такими же, как будто ничего не произошло.
Одинаковые части объекта повторяют друг друга при повороте. Вот это и есть угловая симметрия. Или поворотная, как Вам удобнее.
Ярчайший пример углового баланса – кубик Рубика, который знаком всем с детства. Я думаю, когда мы вертели его в руках, то совершенно не задумывались какая это симметрия. Мы просто наслаждались процессом.
Сетка
Определение «динамической симметрии» впервые упоминается в произведениях Платона. Много позже это понятие появилось в работах у Джея Хэмбиджа. Он первый изобразил сочетание золотого сечения с логарифмической прямой.
Хэмбидж особенно ценил важность диагонали и придумал свою серию динамических прямоугольников, в которой показал, что диагональ прямоугольника, разделяется перпендикулярной линией, опущенной из угла прямоугольника, в пропорциональном соотношении.
На сегодняшний день динамическая симметрия это популярное, вошедшее в историю течение, в котором деятели искусства и творцы не прекращают поиска единства и гармонии в природном формообразовании. Только как это показать в композиции?

Эта одна из многообразий сеток, используемых в фотографии для создания структуры и компоновки кадра. Горизонтальные и вертикальные линии, диагонали задают изображению ритм и гармоничность. Такие сетки применяются во всех сферах искусства – живопись, скульптура, фотография.
«Лаокоон и его сыновья» — греческая античная скульптура, найденная в начале XVI в. на территории современной Италии. Греки и римляне просто обожали равнозначные пропорции. В античном мире симметрию в скульптуре ставили на первое место.
Геометрия в кадре
Все многообразие симметрий и форм, которое мы с вами сегодня обсудили можно свети к одному – нехитрые формы круга, треугольника, квадрата, кривых и прямых линий – это самые лучшие помощники художника.
Эти формы совмещают в себе единичные элементы изображения и цепляют взгляд. Почти в любом объекте окружающим нас можно заметить геометрические формы и фигуры. И все они вызывают в нас разные эмоции.
Быстрее всего наш взгляд фиксирует углы квадрата, а в круге – центр. Так сказать, активные зоны.
Прямые и кривые линии выполняют функцию проводника по изображению. Если с умом подобрать такие направляющие, то сможете, так сказать, управлять взглядом наблюдателя.
Если говорить о треугольниках в фотографии, то использовать лучше неравнобедренные, так как равнобедренные менее динамичны и не притягивают взгляд.
Немного о карандаше
Геометрические формы и симметрия идут рука об руку с искусством на протяжении всей истории. По своей сути геометрия и есть объемное воображение, скованное строгими правилами логики.
В рисунках с изображением геометрических фигур всегда есть что-то захватывающее. Каждый элемент самодостаточен и одновременно связан с остальными. Все линии и формы отвечают строгим правила, и в то же время изображение кажется сумбурным.
Противоположность
Если бы все было идеально, мы бы умерли от скуки. Ни тебе хаотичности, ни разброса, все ровно, строго и понятно. А как же загадка, магия? Думаю, что именно асимметрия в искусстве и порождает подобные мысли. И желание докопаться до сути, идеи и замысла автора. Там есть тайна, не иначе.
Характер, расположение и размер композиции должны подчиняться зрительному равновесию. Баланс хорошей асимметричной композиции выстроен на сложнейшей структуре множества закономерностей, так как ее элементы не объединены точкой (осью) симметрии.
Отсутствие композиционного равновесия в кадре доставляет зрителю неудобства. И пусть две части одного изображения не одинаковы, визуальная масса элементов должна быть равна.
Достичь гармонии и визуального равновесия в асимметричном кадре сложнее, поскольку элементы имеют разную визуальную массу. И тем не менее, несмотря на всю сложность своего строения, такое непропорциональное изображение задерживает на себе взгляд.
Казалось бы, асимметрия — это для тех, то любит нарушать правила, но в хаосе тоже есть порядок. Поэтому такое «нарушение» нормы придаст кадру выразительность и динамику.
Заключение
Геометрические фигуры, симметрия и асимметрия встречаются нами ежедневно — архитектура, еда, природа. Если присмотреться, все, что нас окружает, состоит из фигур и композиций.
Оглядывайтесь по сторонам чаще, наш мир невообразимо прекрасен! Дальше будет еще интереснее. Оставайтесь с нами и не забывайте рассказывать о нас друзьям в соц.сетях.
Пишете в комментариях свои мысли, идеи, размышления, делитесь опытом. Буду признателен за обратную связь. Симметрия настолько сложный и интересный процесс, но он требует погружения и размышления.
Удачных вам находок, и до новых встреч. Иван.
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
Рис. 1 Фигуры, обладающие симметричностью
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.
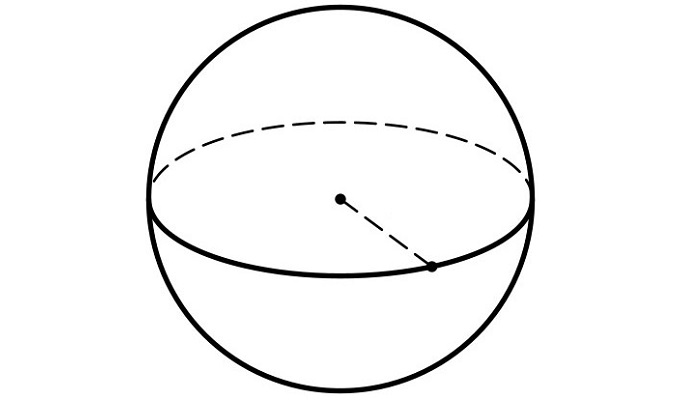
Рис. 2 Графическое представление центральной симметрии
Осевая симметрия
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.
Рис. 3 Наглядное представление осевой симметрии
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.
Рис. 4 Примеры осевой симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
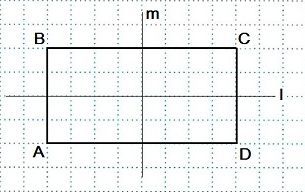
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
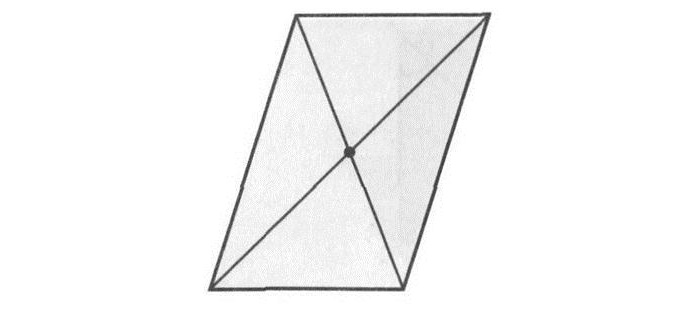
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
Рис. 5 Оси симметрии ромба
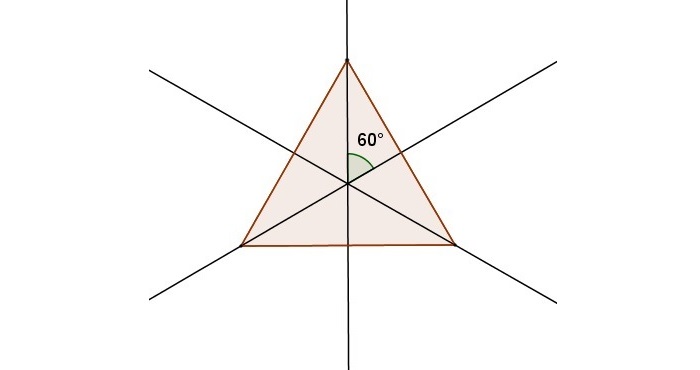
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Осевая и центральная симметрии. Проводим урок с ЭФУ
Повторение материала
Из курса математики 5 класса учащиеся уже узнали, как выглядят и строятся фигуры, имеющие ось симметрии. Перед изучением темы «Осевая и центральная симметрии» будет целесообразно повторить материал 5 класса. Следует разъяснить учащимся, что построение фигуры во многих случаях возможно по положению ключевых точек.
Для закрепления этого интуитивно-наглядного понимания, учитель может предложить детям перегнуть лист бумаги, на котором изображены симметричные фигуры.
Понятие симметрии
Слово «симметрия» происходит от греческого symmetria, что означает соразмерность. В нашем случае, симметрия — это свойство геометрических фигур к отображению.
Учитель: Симметрия используется в рисунках, орнаментах, архитектуре с давних времен. Где еще симметрию могут использовать люди?
Ученики: при строительстве домов; в изготовлении предметов быта.
Учитель: верно, но ведь симметрия распространена не только там, где творил человек! Мы видим симметричные объекты природы каждый день. Назовите мне три таких объекта!
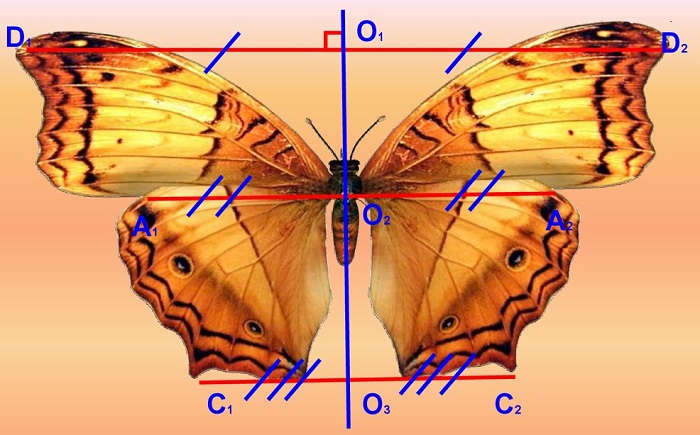
Ученики: Бабочка, цветы, форма листа! Морская звезда, снежинка, яблоко в разрезе.
Симметрий, как это не покажется вам странным и любопытным, много, но мы будем рассматривать две симметрии на плоскости: относительно точки и прямой.
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Заметим, что любые две фигуры, симметричные относительно некоторой прямой, равны (Рис.131). Все точки фигуры, имеющей ось симметрии, не принадлежащие этой оси, можно разделить на пары симметричных точек (Рис. 132).
Центральная симметрия
Симметрию относительно точки называют центральной симметрией.
Фигуры, имеющие центр симметрии — понятие, воспринимающееся учащимися сложнее, чем фигуры, имеющие ось симметрии. Для удобства восприятия и понимания, рекомендуется привести как можно больше примеров из окружающей природы.
В зависимости от уровня математической подготовки учащихся класса, можно обратить их внимание на то, что прямая — это фигура, имеющая бесконечно много осей и центров симметрии.
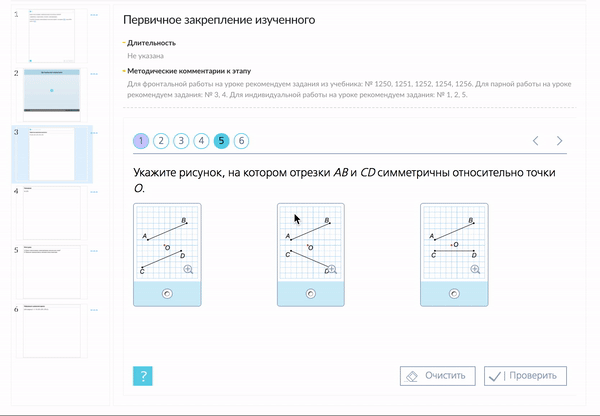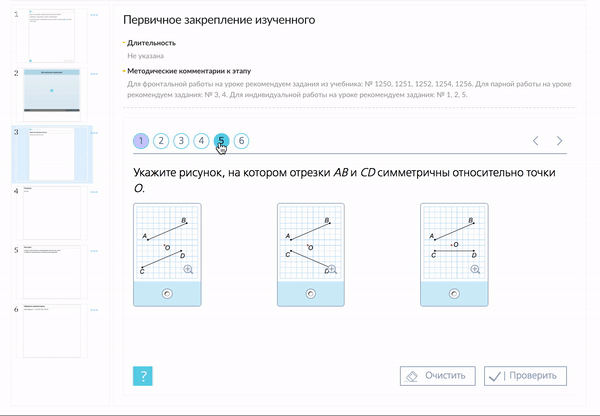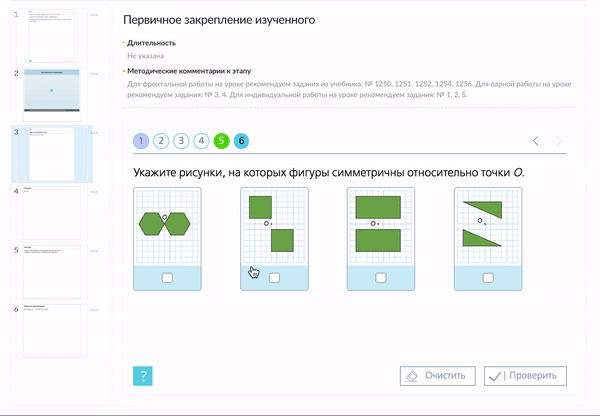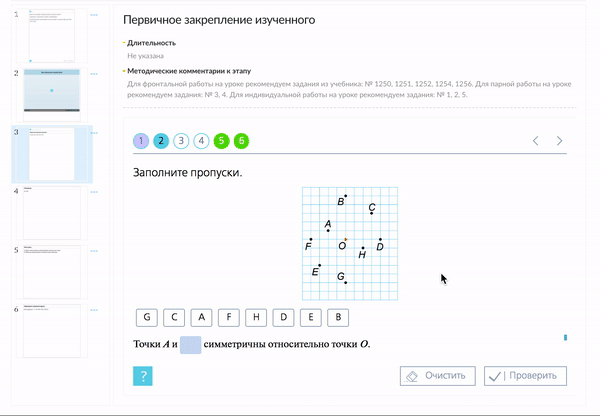
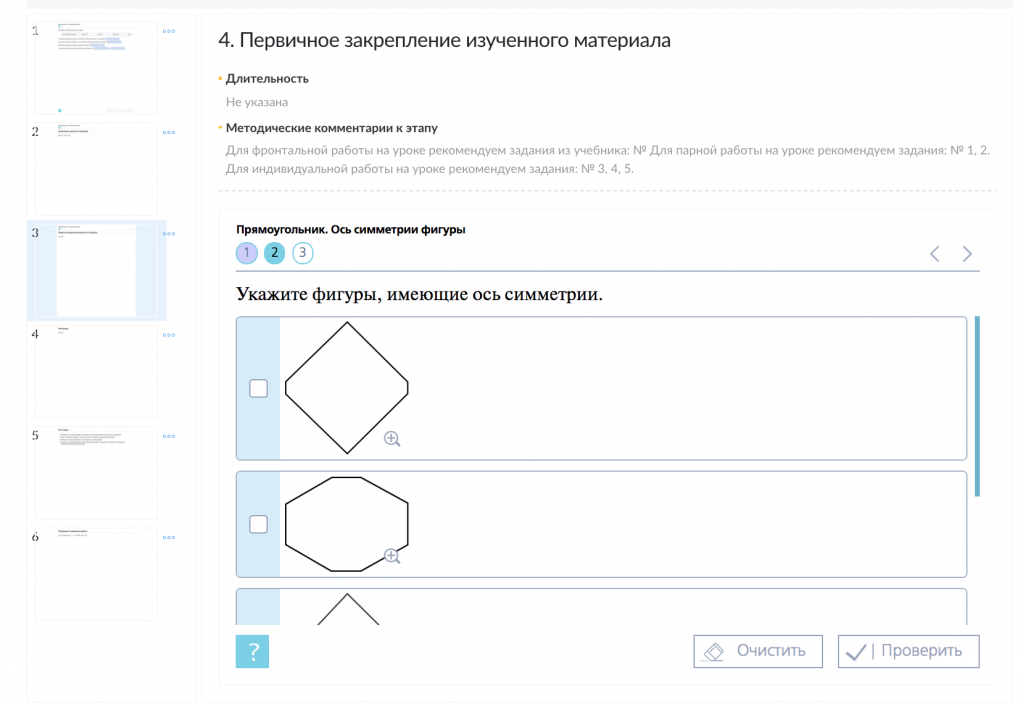
С помощью заданий из «Классной работы» материал можно закрепить в различных графических форматах.
Актуализация знаний
Предложите ребятам решить задание № 1260. Какие печатные буквы русского алфавита имеют 1) вертикальную ось симметрии; 2) горизонтальную ось симметрии; 3) горизонтальную и вертикальную оси?
Готовый яркий раздаточный материал «Алфавит» вы можете скачать в конце этой статьи.
Также рекомендуем вам применять на уроке различные методы преподнесения информации: как визуальный, так и аудио. Попробуйте аудиодиктант.