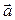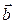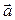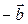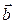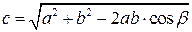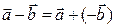Что такое скалярная физическая величина
Скалярная величина
Скалярная величина (от лат. scalaris — ступенчатый) в физике — величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только своим значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д. [1]
Примечания
Полезное
Смотреть что такое «Скалярная величина» в других словарях:
скалярная величина — скаляр Словарь русских синонимов … Словарь синонимов
скалярная величина — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN scalar quantityscalar … Справочник технического переводчика
скалярная величина — skaliarinis dydis statusas T sritis automatika atitikmenys: angl. scalar; scalar quantity vok. skalare Größe, f rus. скалярная величина, f pranc. grandeur scalaire, f … Automatikos terminų žodynas
скалярная величина — skaliarinis dydis statusas T sritis fizika atitikmenys: angl. scalar quantity vok. skalare Größe, f rus. скалярная величина, f pranc. grandeur scalaire, f … Fizikos terminų žodynas
скалярная величина — Syn: скаляр … Тезаурус русской деловой лексики
скалярная проводимость — удельная электрическая проводимость; скалярная проводимость; проводимость Скалярная величина, характеризующая электропроводность среды и являющаяся функцией термодинамических параметров … Политехнический терминологический толковый словарь
колеблющаяся величина — Поочередно возрастающая и убывающая во времени скалярная величина, связанная с описанием и движением механической системы. Примечание В описание механической системы могут входить и силы, действующие в ней. [Сборник рекомендуемых терминов. Выпуск … Справочник технического переводчика
колеблющаяся величина — Поочередно возрастающая и убывающая во времени скалярная величина, связанная с описанием и движением механической системы … Политехнический терминологический толковый словарь
Физическая величина — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Физическая … Википедия
Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия
Скаляры и векторы: что это такое
В физике используется много различных математических величин. Например, ускорение, скорость, сила, работа, мощность и так далее. Ученые делят эти величины на два типа: «скалярные» и «векторные». Что же означают эти типы и чем они отличаются?
Скаляр – это величина, которая описывается только значением. Значение этой величины выражает только число. Примеры скалярных величин: скорость, объем, масса, температура, мощность, энергия, время и т.д. Более о скорости читайте в учебнике по физике за 7 класс В.Г. Баряхтяра.
Вектор – это величина, которая имеет как значение, так и направление. Векторные величины важны при изучении движения. Некоторые примеры векторных величин: сила, скорость, ускорение, перемещение и импульс.
Вектор имеет и направление, и значение, а скаляр имеет только значение. Вы можете сказать, является ли величина вектором, просто если поймете, имеет ли эта величина направление.
Как нарисовать вектор?
Вектор нарисован в виде стрелки с головой и хвостом. Величину вектора часто описывают длиной стрелки. Стрелка указывает в направлении вектора.
Векторы обычно пишутся в виде жирных букв. Они также могут быть написаны в виде стрелки над буквой.
Пример вопросов: скаляр или вектор?
1) Футболист бежал со скоростью 15 км в час по направлению к концу зоны.
Это вектор, так как он представляет и значение (15 км/ч) и направление (по направлению к концу зоны).
2) Температура помещения составляет 15 градусов по Цельсию.
Это скаляр, направления нет.
3) Автомобиль разогнался на север со скоростью 4 м/с2 (четыре метра в секунду в квадрате).
Это вектор, поскольку он имеет как направление, так и величину. Мы также знаем, что ускорение – это векторная величина.
Два вида физических величин: скалярные величины и векторные величины
«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.
Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:
Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что
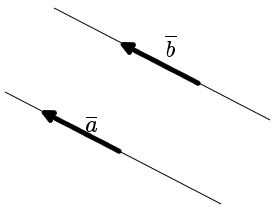
Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.
А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.
Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.
Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.
Какие из представленных на рисунках величин являются скалярными, а какие — векторными?
Скалярные величины, векторные величины и нахождение равнодействующей двух перпендикулярных сил
Физические величины можно разделить на скалярные и векторные величины, скалярная величина — это физическая величина, которая может быть полностью определена только своей величиной и не имеет направления, в то время как векторная величина — это физическая величина, которая может быть полностью определена как величиной, так и направлением.
Примеры скалярных величин: расстояние, масса, время, температура и энергия. Примеры векторных величин : смещение, скорость, ускорение и сила.
При измерении физической величины, такой как температура (величина температуры, скажем, 27 ° C полностью описывает температуру), скорость (значение 20 км / ч не полностью описывает скорость автомобиля, так что направление движения автомобиля должно быть определенным).
Расстояние и смещение
Существует разница между концепцией смещения и концепцией расстояния. Расстояние — это длина пути, пройденного объектом из одной позиции в другую, Расстояние — это скалярная величина, которая может быть полностью определена только по ее величине.
Рекомендации по решению проблем
Представление векторных величин
Некоторые основы и векторная алгебра
Два вектора равны, если они имеют одинаковую величину и одинаковое направление (даже если они имеют разные начальные точки). Два вектора не равны, если они имеют разные направления (даже если они имеют одинаковую величину) или разные величины (даже если они в том же направлении ).
Векторная алгебра
Векторная алгебра, такая как сложение векторов, векторное разрешение, векторное произведение (скалярное (точечное) произведение и перекрестное произведение).
Результат (сложение) векторов
Если камень тянут двумя веревками с двумя силами 30 Н и 40 Н, имеющими угол между ними 90 °, мы замечаем, что камень перемещается на определенное расстояние в направлении, отличном от направления этих двух сил (в течение определенного времени ).
Если две веревки заменить одной веревкой и потянуть с силой 50 Н, мы заметим, что порода перемещается на одинаковое расстояние в одном и том же направлении, когда на нее действуют две силы в одно и то же время.
Это означает, что сила 50 Н производит тот же эффект, что и две силы 30 Н и 40 Н. Таким образом, она считается равнодействующей двух сил 30 Н и 40 Н.
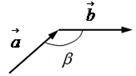
Есть два способа сложить два вектора, нарисовав треугольник и нарисовав параллелограмм, в котором A и B являются смежными сторонами. Таким образом, диагональ представляет их результат.
Нахождение равнодействующей двух перпендикулярных сил
Во-первых: графически
Второй: теоретически
Найдите величину равнодействующей силы, используя теорему Пифагора для прямоугольного треугольника (AC² = AB² + BC²).
Угол (θ) можно найти по соотношению
tan θ = F y / F x = F 2 / F 1
Разрешение вектора
Разрешение вектора — это обратная операция для получения равнодействующей некоторых векторов, где сила может быть разделена на две перпендикулярные силы по размерам (x, y), Таким образом:
Произведение векторов
Существуют разные формы нахождения произведения двух векторов:
Скалярное (точечное) произведение
Скалярное произведение двух векторов A и B выражается следующим образом:
Знак (.) Произносится как «точка». Результат — скалярная величина.
Работа — это скалярная величина, поскольку она является скалярным произведением двух векторов силы и смещения, W = F. d, Если вектор (F) действует на вектор (d) под углом (θ).
Векторное (перекрестное) произведение
Перекрестное произведение двух векторов A и B выражается следующим образом:
C = A ^ B = AB sin θ n
Где n — единичный вектор, перпендикулярный плоскости обоих векторов A и B, знак (^) произносится как крест, и результатом является векторная величина C, вектор C указывает на направление n, перпендикулярное плоскости обоих векторов. А и Б.
Работа электродвигателя зависит от наличия двух векторов, а именно электрического поля и магнитного поля, которые вызывают вращение катушки двигателя в направлении, перпендикулярном их плоскости.
Правило правой руки
Он используется для определения направления векторного произведения C двух векторов A и B.
Скалярные и векторные величины



Скалярная величина – это физическая величина, которая имеет только одну характеристику – численное значение.
Скалярная величина может быть положительной или отрицательной.
Примеры скалярных величин: температура, масса, объем, время, плотность. Математические действия со скалярными величинами – это алгебраические действия.

1) численное значение, которое всегда положительно (модуль вектора);
Примеры векторных физических величин: скорость, ускорение, сила.
Векторная величина обозначается латинской буквой и стрелкой над этой буквой. Например:
— вектор скорости обозначается символом 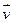
— вектор ускорения обозначается символом 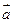
— вектор силы обозначается символом 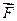
Модуль вектора обозначается так:
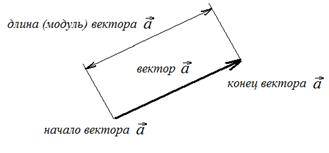
На рисунке (графически) вектор изображается направленным отрезком прямой линии. Модуль вектора равен длине направленного отрезка в заданном масштабе.
Действия с векторами
Математические действия с векторными величинами – это геометрические действия.
Сравнение векторов
Равные векторы. Два вектора равны, если они имеют:
Противоположные векторы. Два вектора противоположны, если они имеют:
Сложение векторов
Мы можем сложить два вектора геометрически по правилу параллелограмма и по правилу треугольника.
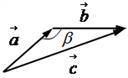
Пусть заданы два вектора 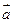
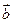
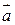
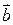
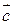
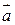
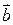
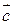
Правило параллелограмма для сложения двух векторов:
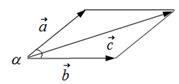
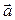
2. Нарисуем вектор 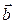
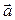
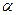
3. Через конец вектора 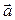
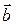
4. Через конец вектора 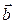
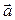
Мы построили параллелограмм. Стороны этого параллелограмма – составляющие векторы 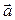
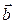
5. Проведем диагональ параллелограмма из общей точки начала вектора 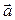
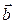
6. Модуль результирующего вектора 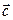
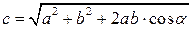
начало вектора 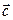
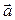
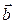
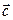
Правило треугольника для сложения двух векторов:
1. Нарисуем составляющие векторы 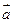
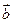
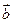
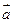
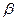
2. Результирующий вектор 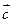
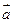
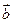
3. Модуль результирующего вектора находим по формуле:
Вычитание векторов
Вычитание векторов – это действие, обратное сложению:
Найти разность вектора